基于问题表征的物理习题解决探析

陈 燕

(南京航空航天大学苏州附属中学 江苏 苏州 215000)

1 物理习题的特征

物理习题是指由一个或若干个学科原理，以一个或若干个能承载学科原理的物理情景，将学科原理中所涉及的某些物理量或物理量之间存在的某些内在联系以间接的表征方式予以呈现，进而构成具有“知识锁链脱节”特征的物理问题.物理习题构成的基本要素包括学科性、情景性和间接性，主要问题特征在于“知识与认知锁链的脱节”.

2 物理问题表征

表征是指信息或知识在人脑中的呈现或记载方式.问题表征是指把已知的问题转化为内在的心理表象，经过大脑的加工，将内隐的知识外显化.问题解决的过程就是运用物理问题解决策略去实现对问题完全表征的过程，即问题表征不只是一个环节和阶段，而是涵盖从呈现问题到解决问题、贯穿问题解决过程始终的动态的认知过程，对问题能否顺利解决起着至关重要的作用.西南师大的廖伯琴教授在著名物理教育家麦克德莫特(McDermott)和拉金(Larkin)提出的物理问题解决表征层次理论基础上，进行了物理问题表征的动态和静态研究，将物理问题表征分为文字表征、朴素表征、物理表征和数学表征4个层次

3 物理习题解决的问题表征

3.1 文字表征阶段

文字表征阶段，是关于问题文字描述的理解，通俗讲就是“审题”，即辨认解题情境，在头脑中建立题目结构的特征.在认知心理学中，审题称为问题的表征，把物理属性抽象出来是审题的特征，审题的核心过程是实现由题目文字(符号)表述到题目物理条件和问题的转化，实际上是把问题中的每一个陈述转换成解题者内部心理表征的过程.

学生解题过程中最常见的障碍之一是“不知道如何分析复杂物理现象，面对习题中的复杂现象不知如何下手”.习题中的各种条件具有无序性，解题的过程实质上就是把题中处于无序状态的条件逐步组织起来，建立待求量与已知量(条件)之间联系的过程.将物理习题中审题表征为常见的实物条件、量值条件、动变特征条件、数量关系条件和图像条件，这些条件制约着解题的方向和具体路径[2].

(1)实物条件

物理试题的命制一般都是某个特定情境的物理实物系统，该系统由不同空间位置分布的两个或更多的物理实体构件(包括重力场、电场、磁场)构成，各个构件和它们构成的整个实物系统组成了物理试题的实物条件.

(2)量值条件

物理试题中的量值条件一般是以数值或字母形式给出的已知物理量值或数学量值，是试题中数量最多的一种已知条件.按照量值反映特征的不同，把量值条件大体划分为描述实物构件的固有物理性质的属性量，描述实物对象(构件)状态特征的状态量，描述实物对象间相互作用特征及强弱的作用量，描述实物构件间相对方向、位置和过程所经历时间的基本变量4种类别.

(3)动变特征条件

动变特征条件是指通过定性的物理语言以及图形形式描述的说明实物系统中各构件间相互作用状况、运动状况和状态变化特点的条件.

(4)数量关系条件

数量关系条件是解题过程中利用的物理量之间的数量关系，常以和差积商等形式或补充方程式出现.

(5)图像条件

物理试题中的某些条件是通过物理函数图像直接或间接提供的，解题过程中须运用图像的知识，根据图像的特定点(横纵坐标轴上截距点、极值点、图线交点等)，图像中的“线”与坐标轴间包围的面积等，获取对应的量值条件.

【例1】(2015年高考全国理综Ⅰ卷第2题)一长木板置于粗糙水平地面上，木板左端放置一小物块；在木板右方有一墙壁，木板右端与墙壁的距离为4.5 m，如图1(a)所示，t=0时刻开始，小物块与木板一起以共同速度向右运动，直至t=1 s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变，方向相反；运动过程中小物块始终未离开木板.已知碰撞后1 s时间内小物块的v-t图线如图1(b)所示.木板的质量是小物块质量的15倍，重力加速度大小g取10 m/s2.求：(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2；(2)木板的最小长度；(3)木板右端离墙壁的最终距离.

图1 例1题图

根据题意的条件分析得：

(1)实物条件.长木板、小物块、地面(地球)；

(2)量值条件.木板右端与墙壁的距离为4.5 m，重力加速度大小g取10 m/s2；

(3)动变特征条件.t=1 s时木板与墙壁碰撞，碰撞前后木板速度大小不变，方向相反，运动过程中小物块始终未离开木板；

(4)数量关系条件.木板的质量是小物块质量的15倍；

(5)图像条件.碰撞后1 s时间内小物块的v-t图线，即做加速度a=4 m/s2的匀减速运动.

3.2 朴素表征阶段

朴素表征阶段是根据问题的表面特征和生活经验对问题整体结构和框架的理解.物理习题的情境是承载特定学科原理的物理事件，命题者借助千变万化的情境承载同一物理问题，或通过一个或多个情境呈现相关的学科原理信息.在解题活动过程中，学生仅依靠习得的物理基础知识还不够，需建立已有的知识与表征题目的语言文字所表示的内容之间相互作用的联系，将习题所描述的物理现象译成物理情境图像输入大脑暂时储存，然后大脑进行一系列复杂的心理操作，在大脑中形成一系列合理的条件化的物理表征结构，将物理语言表述与具体表象经验进行联结.

历年高考试题背景中的STSEL(科学·技术·社会·环境·生活)类情境素材常以多样性、复杂性和综合性呈现，表现为“生活化情境、学术化描述、数学化思维”.《普通高中物理课程标准(2017年版)》“学业水平考试与命题建议”中提出：“试题的情境要具有一定的问题性、真实性、探究性或开放性”.

例如2019年高考天津卷第2题港珠澳跨海大桥其索塔与钢索的受力分析.第4题笔记本电脑机身和显示屏对应部位分别有磁体和霍尔元件分析等.对试题情境的表征涉及考生的熟悉程度、可理解性以及考生的潜在水平.《普通高中物理课程标准(2017年版)》“学业水平考试与命题建议”中提出：“考试内容的任务情境应符合学生心理发展水平和认知规律，反映物理学科本质，密切联系社会、经济、科技、生产生活实际”[1].

3.3 物理表征阶段

物理表征是“透过现象看本质"的阶段，是对问题深层特征的把握.物理表征的关键是对问题表征的物理建模.

物理核心素养中“科学思维”部分关于物理模型建构与运用的水平层次划分如表1所示.

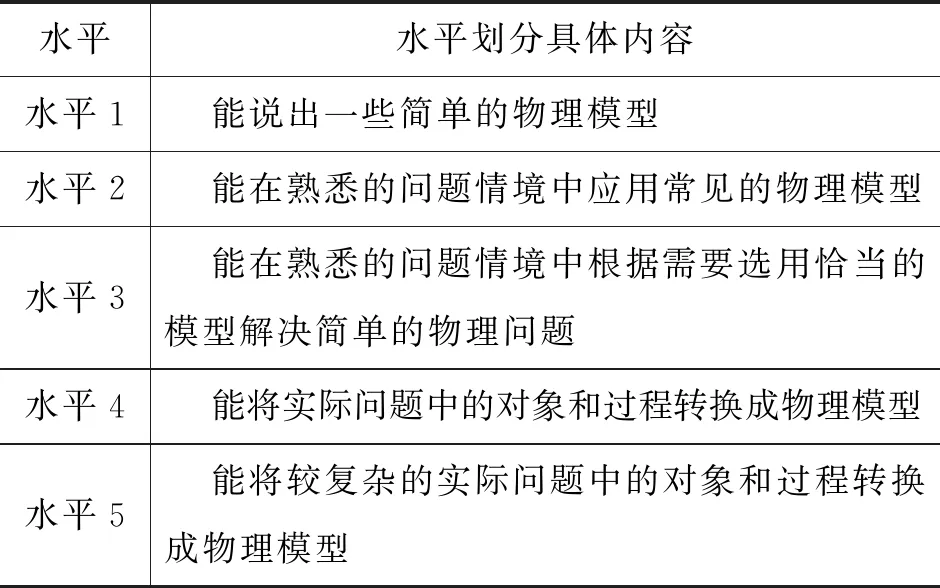
表1 物理核心素养中“科学思维”部分关于物理模型建构与运用的水平层次划分

水平层次划分了学生对物理建模由浅到深的理解与应用的不同程度.然而在物理习题教学过程中，学生的物理建模思维训练过程被习题编制者“越俎代庖”，导致学生只会死记硬背式的“套模”，而不会随实际问题情境变化进行灵活的物理“建模”.以轻质模型(常见有轻绳、轻杆、轻弹簧模型)为例.

【例2】(2011年高考江苏卷第9题)(轻绳模型)如图2所示，倾角为α的等腰三角形斜面固定在水平面上，一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧，绸带与斜面间无摩擦.现将质量分别为M,m(M>m)的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等，且最大静摩擦力与滑动摩擦力大小相等.在α角取不同值的情况下，下列说法正确的有( )

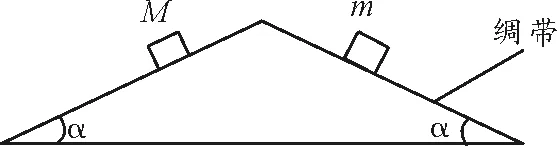
图2 例2题图

A．两物块所受摩擦力的大小总是相等

B．两物块不可能同时相对绸带静止

C．M不可能相对绸带发生滑动

D．m不可能相对斜面向上滑动

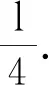
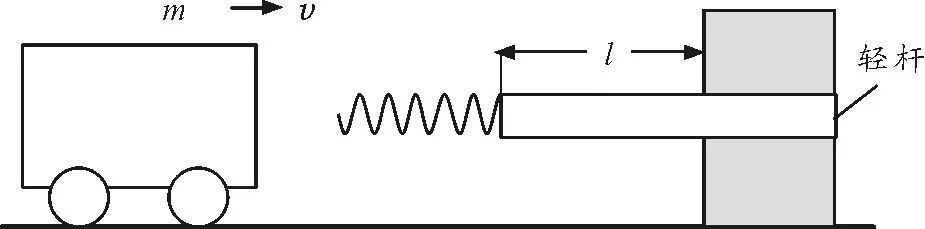
图3 例3题图

(1)若弹簧的劲度系数为k，求轻杆开始移动时，弹簧的压缩量x；

(2)求为使装置安全工作，允许该小车撞击的最大速度vm；

(3)讨论在装置安全工作时，该小车弹回速度v′和撞击速度v的关系.

部分学生没有认识到例2中轻绳模型的本质：轻质绸带质量不计，由牛顿第二定律得到轻质绸带所受合力必为零，则M与m对绸带的摩擦力必大小相等，方向相反.例3中涉及“轻杆模型”“弹簧模型”，学生最大的思考障碍在于对“轻杆模型”和“弹簧模型”的建立和应用，轻杆没有质量，就没有惯性，速度可以突变，轻弹簧与轻杆都属于轻质模型，轻质模型的本质是“质量为零，所受合力必为零”，模型表征分析是解决问题的关键点.教师应在平时教学过程中引导学生展开对物理模型的本质研究，澄清学生头脑中对物理模型“似是而非”的认识误区，避免学生对物理模型的问题解决采用“回忆”替代“分析”.

3.4 数学表征阶段

数学表征，是用数学公式表征物理规律以及运用它们进行数学推导的过程.这与问题解决者所使用的数学工具有关，可以反映问题解决者的数学功底.试题中的各种条件具有无序性，解题的过程实质上就是把题中处于无序状态的条件逐步组织起来，建立待求量与已知量(条件)之间联系的过程.“公式环”是根据物理公式建立的关联环.通过“公式环”，把题中的几个物理量按照公式固有的数学形式联系起来.

将上述4个阶段联结起来如图4所示.研究表明问题解决过程中对问题表征不完善或错误就是试误，需重新表征.4个表征层次之间并不是呈线性发展的，在问题解决的每一表征阶段都有可能发生新的问题，问题表征是一个不断完善的、动态的发展过程.通过问题表征训练，改善问题解决过程中“一听就懂，一看就会，一做就错”的现象，活化优化学生的物理认知结构，从而提高物理问题解决的能力.

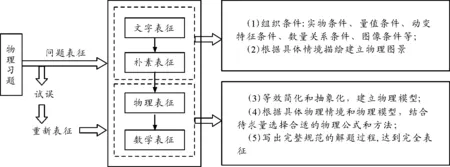
图4 物理习题问题表征和解决的全程导图