基于分形理论的玄武岩筋废旧钢纤维混凝土梁受弯性能研究
2020-08-12范小春袁云林
范小春,吴 伟,袁云林
(1.武汉理工大学土木工程与建筑学院,武汉 430070;2.新十建设集团有限公司,武汉 430070)
0 引 言
纤维增强聚合物(Fiber Reinforced Polymer,FRP)筋是一种高性能的新型筋材,在混凝土结构中有广泛应用前景[1]。其中玄武岩(BFRP)筋因其高性价比、高强度和耐腐蚀等优势,得到工程界广泛认可[2-4]。但由于FRP筋弹性模量低、线弹性等特征,导致FRP筋混凝土结构多伴随裂缝较宽和变形较大等缺陷,使其在实际工程中的应用存在局限性。国内外有学者通过在混凝土中掺入工业钢纤维来改善这一问题[5-7]。同时,有研究表明回收废旧轮胎中的钢纤维(Recycled Steel Fiber,RSF),将其替代传统工业钢纤维是降低钢纤维混凝土成本和改善废弃轮胎带来的环境污染问题的有效方法[8-11],但有关废旧钢纤维混凝土的报道仍集中于基本力学性能研究。因此,对FRP筋废旧钢纤维混凝土结构力学性能的研究具有深远意义。
分形几何学(Fractal Geometry)是研究自然界不规则几何图形的有效手段,运用分形理论可对混凝土结构表面裂缝的演化进行定量分析,为研究其力学性能提供新方法。目前,许多国内外学者运用分形理论对混凝土表面裂缝展开了研究。Viktor[12]运用分形理论对混凝土的断裂性能进行研究,结果表明混凝土断裂面粗糙程度和裂缝形态均与混凝土的非匀质性直接相关。Alireza等[13]通过分形理论对混凝土表面裂缝进行了分析,发现混凝土表面裂缝的曲率和粗糙度均满足自相似性。李艳艳等[14]通过对高强箍筋混凝土梁受剪过程中产生的裂缝进行分形特征描述,发现分形维数可以用来表征裂缝的分布情况和梁损伤程度。栾海洋等[15]通过模拟腐蚀环境,对弯曲荷载下试验梁表面裂缝的演化过程进行分形分析,得出损伤深度可由裂缝分形维数来反映的结论。秦子鹏等[16]对BFRP布加固钢筋混凝土梁的受弯性能进行分形特征研究,结果表明同种加固条件下极限荷载、延性系数与分数维数之间均呈线性关系。然而,有关BFRP筋废旧钢纤维混凝土梁受弯性能分形特征的研究还鲜有报道。
本文基于BFRP筋废旧钢纤维混凝土梁的受弯试验结果,对试验梁表面裂缝演化特征和分布形态进行分析,验证受弯过程中BFRP筋废旧钢纤维混凝土梁表面裂缝的分形特征;得到不同废旧钢纤维体积掺量和BFRP筋配筋率下,试验梁表面裂缝分布的分形维数;探讨荷载等级、跨中挠度与分形维数之间的关系;分析废旧钢纤维体积率和配筋率对裂缝分形维数的影响。为BFRP筋废旧钢纤维混凝土结构在实际工程中的应用提供理论依据。
1 实 验
1.1 实验材料
水泥采用华新水泥生产的P·O 42.5普通硅酸盐水泥,粗骨料采用级配良好、直径为5~20 mm的碎石,细骨料采用细度模数为2.80的天然河沙,减水剂选用聚羧酸型减水剂。混凝土的配合比见表1。废旧钢纤维的体积率分别采用0%、0.5%、1.0%、1.5%。玄武岩筋采用江苏省绿材谷新材料科技发展有限公司生产的直径分别为8 mm、10 mm和12 mm的深螺纹玄武岩筋,钢筋选用直径为6 mm的HPB300型钢筋。筋材的物理及力学性能见表2。废旧钢纤维是从废旧轮胎中回收得到的钢纤维,其基本物理参数和力学性能见表3。

表1 混凝土配合比Table 1 Mix proportion of the concrete /(kg/m3)

表2 筋材物理及力学性能Table 2 Physical and mechanical properties of reinforced member

表3 废旧钢纤维物理及力学性能参数Table 3 Physical and mechanical properties of RSF
1.2 试验梁设计
制作5根BFRP筋废旧钢纤维混凝土梁和1根不掺废旧钢纤维的对照组梁,梁尺寸为120 mm×200 mm×2 000 mm,混凝土保护层厚度为20 mm。架立筋和箍筋均选用直径6 mm的HPB300型钢筋,箍筋间距为100 mm。梁基本参数见表4,其配筋示意图如图1所示。

图1 梁配筋示意图(单位:mm)Fig.1 Reinforcement schematic diagram of the beams(unit:mm)

表4 梁基本参数Table 4 Basic parameters of the beams
Note: take B8R05 as an example, BFRP diameter is 8 mm, BFRP bar volume ratio is 0.5%.
1.3 试验加载方案
试验选用500 kN压力机,依据GB/T 50152—2012《混凝土结构试验方法标准》,采用四点弯曲加载方式,加载步距为5 kN一级,当荷载接近开裂荷载计算值时,将加载步距改为0.5 kN一级,每级荷载持荷5 min,试验梁加载测点布置及装置如图2和图3所示。
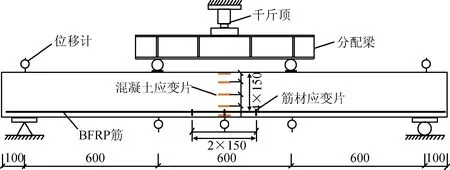
图2 试验装置及测点布置(单位:mm)Fig.2 Loading device on measuring points(unit:mm)

图3 现场加载装置图(B8R00)Fig.3 Loading experiment on site(B8R00)
2 裂缝特征的分形描述
2.1 梁表面裂缝开展过程及分布形态
在梁受弯过程中对其表面的裂缝进行绘制,试验梁表面裂缝的开展过程及分布形态如图4所示。
由图4可知,随着废旧钢纤维的掺入,梁表面的裂缝数有所增加,但单条裂缝在演化过程中的分支却逐渐减少,这表明废旧钢纤维的掺入使得梁受拉区混凝土的受力更加均匀,梁表面的裂缝分布也更加均匀;梁表面裂缝分布的复杂程度随着配筋率的增大而逐渐提高。试验梁的开裂荷载和极限荷载见表4。

图4 试验梁表面裂缝的演化过程和分布形态描绘图,(*)表示裂缝编号,按产生先后顺序标出,**表示加载值Fig.4 Evolution process and distribution forms of beam surface cracks, (*): the number of cracks; **: the values of loading
2.2 裂缝分形维数的计算
分形理论可用来分析具有分形特征的图形,若图形具有分形特征表示其在一定标度范围内满足自相似性。荷载作用下玄武岩筋废旧钢纤维混凝土梁表面裂缝的分布形态是随机的,需要验证才能知道其是否满足分形特征。作为分形理论的重要参数,分形维数可用来表示复杂形体的不规则程度以及反映工程中复杂几何形体及路径等占有空间的有效性[17-18]。分形维数的确定方法一般有标尺法、盒计数法和分岛法[15-16]。文中采用盒计数法测得试验梁表面裂缝的分形维数,方法如下:用边长为r(单位:mm)的网格覆盖试验梁表面,统计出包含裂缝的总格子数,记为N(r),通过改变r得到对应的N(r)值,计算并拟合lnN(r)-ln(r)关系曲线,若两者符合线性关系,则表明梁表面的裂缝分布满足自相似性,可以利用分形理论来研究。梁表面裂缝的分形维数用Df表示,可由式(1)得到。
(1)
2.3 受弯过程中梁表面裂缝的分形特征
用盒计数法对各级荷载下梁表面的裂缝图进行统计,拟合得到相应荷载等级下的lnN(r)与ln(r)关系曲线,如图5所示。
由图5可知,不同荷载等级下试验梁表面裂缝的lnN(r)与ln(r)关系曲线呈明显线性关系,表明加载过程中,梁表面裂缝的演化及分布满足自相似性。lnN(r)与ln(r)关系曲线的斜率代表分形维数Df,受弯过程中试验梁表面裂缝的分形维数Df见表5。
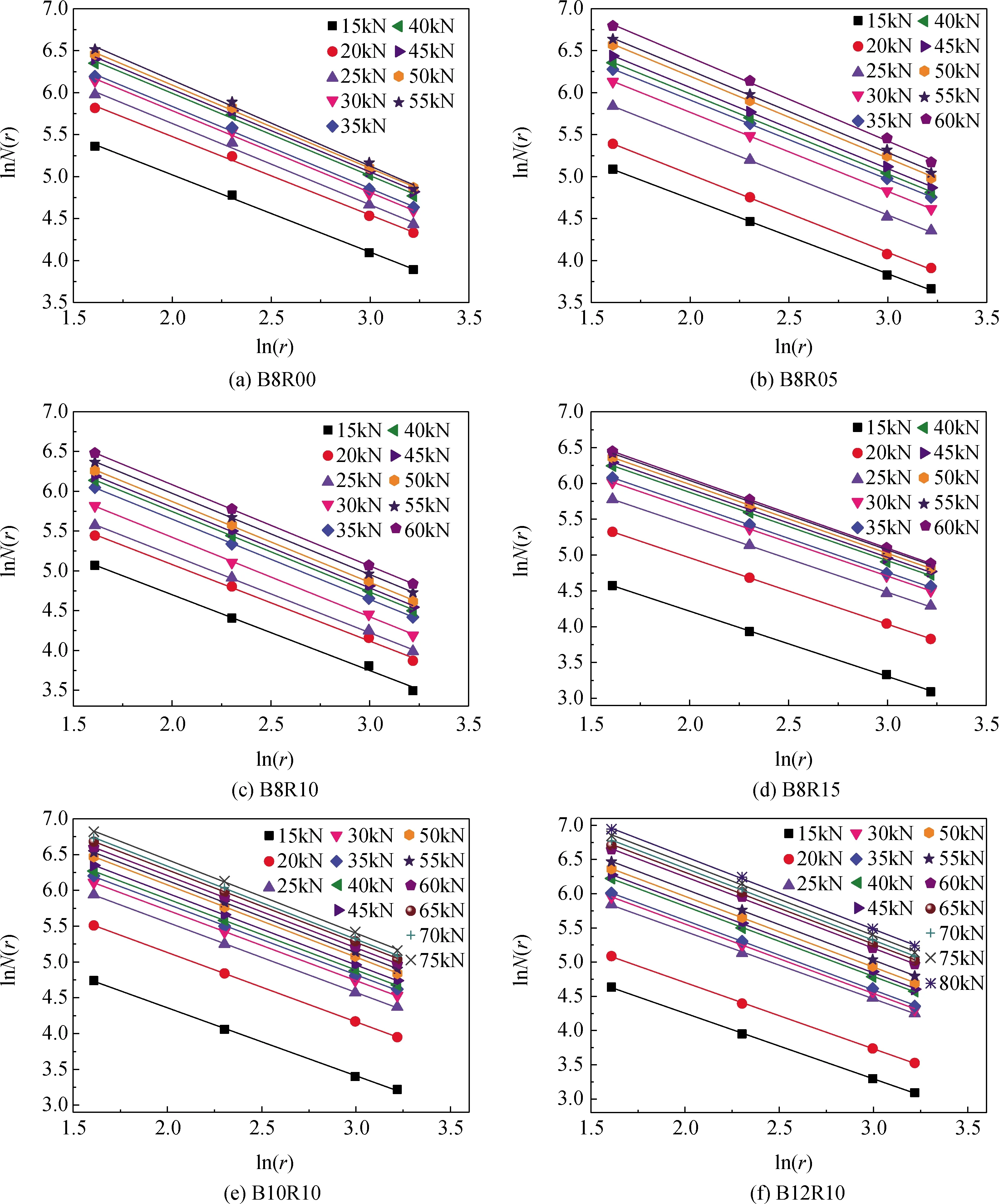
图5 各级荷载下梁的lnN(r)与ln(r)关系Fig.5 Relationship between lnN(r) and ln(r) of the beams under every load grades
从表5可知,随着废旧钢纤维体积掺量和玄武岩筋配筋率的改变,其表面裂缝分形维数也随之发生改变。对同一梁而言,随着荷载等级的增加,其裂缝分形维数也逐渐增大。对于不同废旧钢纤维体积掺量和配筋率的梁,梁表面裂缝分形维数越高,对应试验梁的破坏程度越大。6组试验梁裂缝的分形维数在0.89~1.07变化范围内。

表5 各级荷载等级下梁侧面裂缝的分形维数Table 5 Fractal dimensions of beam surface cracks under every load grades
2.4 极限状态下梁表面裂缝的分形特征
极限荷载下梁表面的裂缝充分发展,拟合极限状态下梁表面裂缝的lnN(r)与ln(r)关系曲线,如图6所示。显然,极限状态下试验梁表面裂缝满足自相似性,极限状态下试验梁裂缝分形维数Df如图7所示。

图6 极限荷载下试验梁的lnN(r)与ln(r)关系曲线Fig.6 Relationship between lnN(r) and ln(r) of the beams under ultimate load
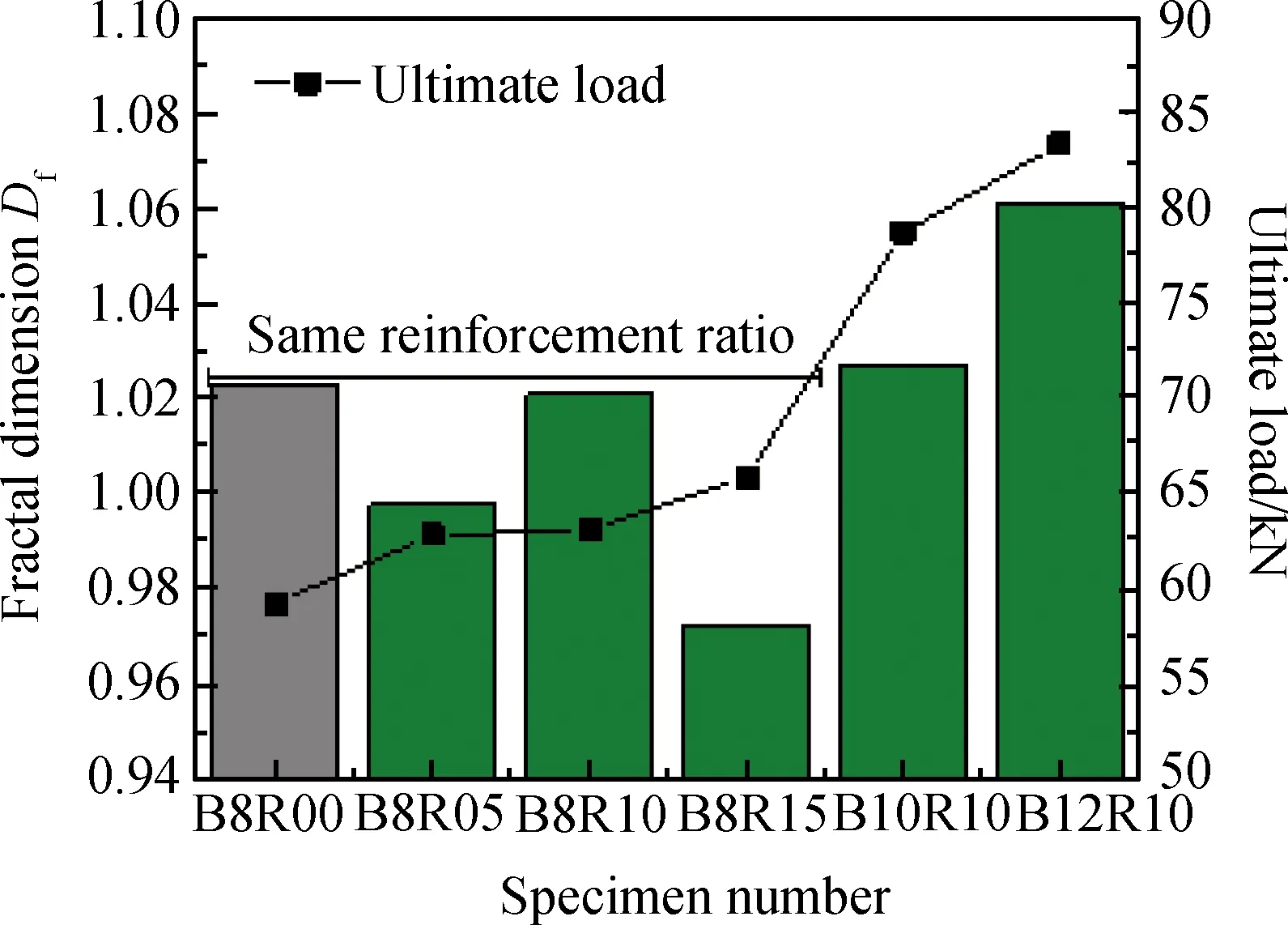
图7 极限荷载下试验梁的分形维数Fig.7 Fractal dimensions of beams under ultimate load
由图7可知,相同配筋率下,随着废旧钢纤维的掺入梁表面裂缝的分形维数有所减小,这表明掺入废旧钢纤维起到了限制梁表面裂缝开展的作用;极限状态下,当废旧钢纤维体积掺量为1.5%时,梁表面裂缝分形维数最小,为0.972 2;当废旧钢纤维体积掺量不变时,裂缝分形维数和梁极限承载力均随着配筋率的提高而逐渐增大。
3 裂缝分形特征与抗弯性能之间的关系
3.1 裂缝分形维数与荷载的关系
由上述分析可知,加载过程中梁表面裂缝具有分形特征,由表5中数据拟合玄武岩筋废旧钢纤维混凝土梁表面裂缝分形维数与荷载等级的关系曲线,如图8所示。
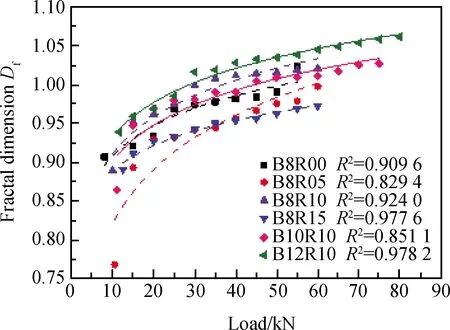
图8 试验梁表面裂缝分形维数与荷载关系曲线Fig.8 Relationship between fractal dimensions and load
由图8可知,玄武岩筋废旧钢纤维混凝土梁表面的裂缝分形维数与荷载等级之间均呈对数增大关系,其关系式如式(2)所示。
Df=Aln(F)+B
(2)
式中,Df表示梁表面裂缝分形维数,F表示荷载等级,A和B值见表6。
由表6可知,试验梁刚到达开裂荷载时,相同配筋率下未掺废旧钢纤维的玄武岩筋普通混凝土梁表面裂缝的分形维数更大;当废旧钢纤维掺量不同时,曲线变化规律差异较大;当废旧钢纤维体积掺量不变时,曲线变化率随着配筋率的增加而逐渐减小。上述现象表明,掺入废旧钢纤维对玄武岩筋混凝土梁的开裂有一定限制作用。

表6 试验梁裂缝分形维数和荷载关系曲线的A和B值Table 6 A and B values of the relationship curves between the fractal dimensions and load
3.2 裂缝分形维数与跨中挠度的关系
统计梁在各级荷载下对应的跨中挠度值与分形维数,拟合Df-Δ关系曲线,如图9所示。
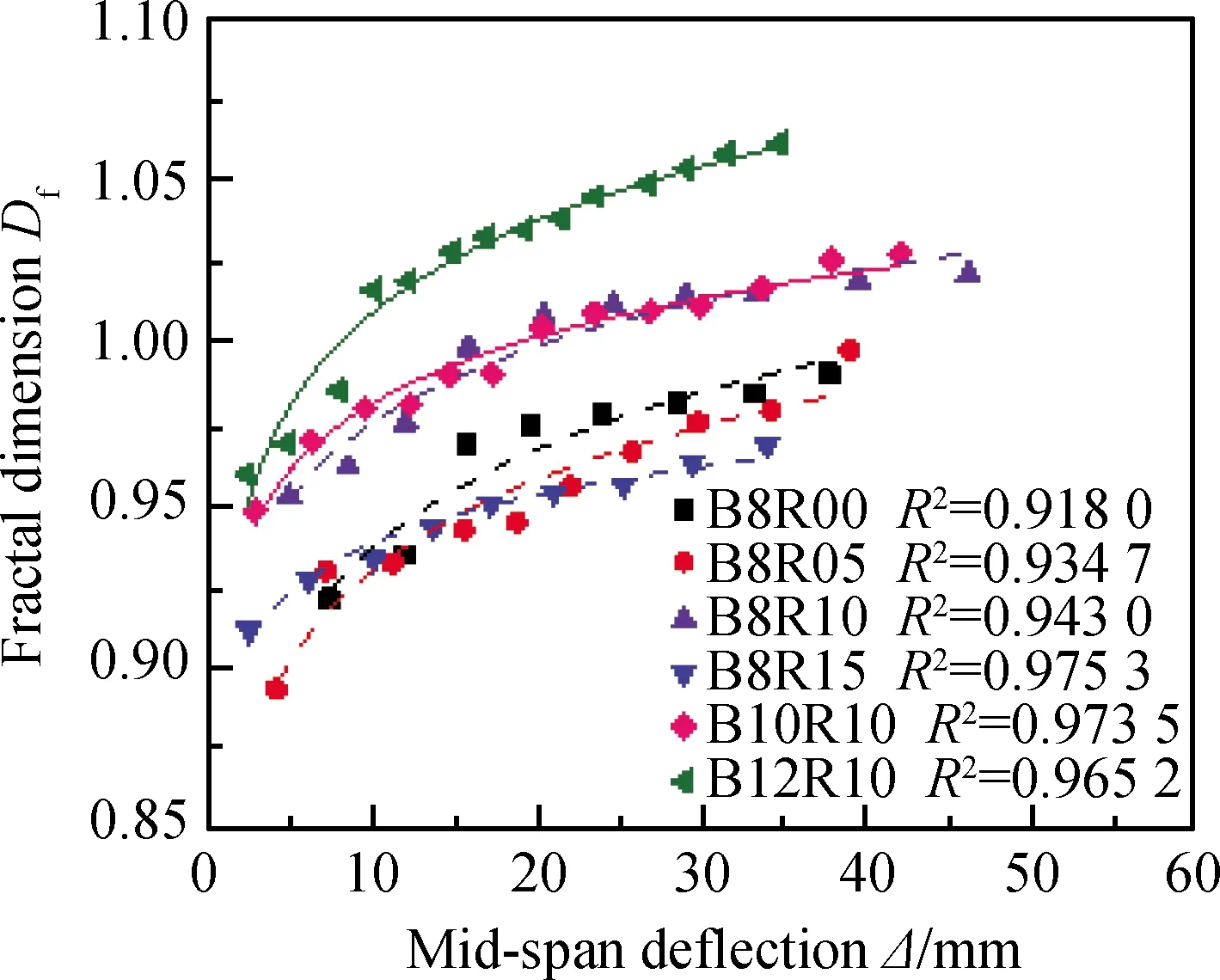
图9 试验梁表面裂缝分形维数与跨中挠度的关系Fig.9 Relationship between fractal dimensions and mid-span deflection
由图9可以看出:梁表面裂缝分形维数Df随着跨中挠度Δ的增大而逐渐增大,两者同样呈对数增长关系,其关系见式(3)。
Df=Cln(Δ)+D
(3)
式中,Df表示梁表面裂缝分形维数,C和D值见表7。
由表7可以看出,当配筋率相同时,随着废旧钢纤维体积掺量逐渐增大,Df-Δ关系曲线的上升趋势逐渐减缓,这是因为废旧钢纤维的掺入改善了同等变形情况下玄武岩筋混凝土梁表面裂缝的开展;当废旧钢纤维掺量不变时,在同等挠度变形情况下随着配筋率的增大梁表面裂缝分形维数也更大,表明梁表面裂缝发展得更充分。

表7 试验梁裂缝分形维数和跨中挠度关系曲线的C和D值Table 7 C and D values of the relationship curves between the fractal dimensions and mid-span deflection
4 结 论
(1)玄武岩筋废旧钢纤维混凝土梁表面裂缝在受弯过程中和极限状态下均具有分形理论的自相似性,满足统计意义上的分形特征,其Df在0.89~1.07之间。
(2)受弯过程中,随着废旧钢纤维体积率的增加,试验梁受拉区混凝土的受力更加均匀,梁表面的裂缝分布也更加均匀。
(3)极限状态下,当玄武岩筋配筋率相同时,废旧钢纤维的掺入减小了梁表面裂缝的分形维数,表明在玄武岩筋普通混凝土梁中掺入适量废旧钢纤维可以起到限制裂缝开展的作用。随着配筋率的增加,梁表面裂缝发展更充分,其分形维数也更大。
(4)玄武岩筋废旧钢纤维混凝土梁表面裂缝分形维数与荷载等级、跨中挠度之间均呈指数增长关系,且拟合函数形式相似。
