基于ADAMS的火箭分离机构动力学分析及仿真
2020-08-12颜驿濛朱冠宁
陈 力,张 明,颜驿濛,朱冠宁
(南京航空航天大学飞行器先进设计技术国防重点科学实验室,江苏 南京 210016)
火箭分离系统是火箭顺利执行分离任务的重要保证,它将直接影响分离体分开后的轨迹[1]。在分离过程中,分离体的姿态角和姿态角速度的改变要尽量小,两个分离体之间不能发生碰撞。如果达不到这些要求,就会导致姿态不可控制、结构损坏等,最终致使任务失败。因此,分离的时机和对分离机构的控制就显得尤为重要。分离系统集成了机械结构、电气控制和液压传动等多个分系统,各个分系统的研制、全系统的整合调试都会对分离任务的实现产生决定性的影响。
火箭在飞行过程中的分离主要包括整流罩分离、星箭分离、级间分离和助推器分离等[2]。分离机构是火箭分离系统中非常重要的部分,分离机构的功能是将火箭飞行过程中已完成预定工作的部分抛掉,这些部分如果不抛弃,就会影响火箭的继续飞行,降低火箭的有效载荷,影响火箭的质量特性。因此,研究火箭分离机构在分离过程中的动力学特性就显得非常重要。
1 火箭分离机构动力学模型
1.1 分离机构动力学分析
以火箭分离机构为研究对象,利用拉格朗日乘子法[3]建立基于ADAMS的系统运动微分方程:
(1)


在对动力学方程进行求解时,式(1)可以改写为:
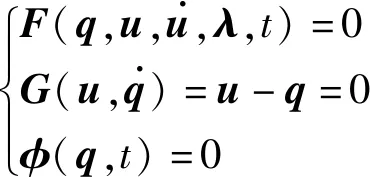
(2)

1.2 分离机构虚拟样机的建立
根据火箭分离机构的总体设计指标,依据分离机构的几何尺寸,通过多体系统动力学软件ADAMS建立了分离机构的虚拟样机[4]。其中分离机构整流罩模型如图1所示。

图1 整流罩模型图
分离机构箭体模型如图2所示。

图2 箭体模型图
火箭分离机构由整流罩与箭体两个部分组成,在ADAMS中建立的完整模型如图3所示。

图3 火箭分离机构模型图
箭体的头部被整流罩包在内部,在分离过程中,整流罩先从箭体弹头中纵向拔出,接着在分离推力的作用下被侧向推离。因此,分离机构的分离仿真过程主要围绕整流罩和下面箭体的头部,分析整流罩和箭体头部是否会发生接触或者碰撞。
2 分离机构的计算载荷
分离体在不同阶段主要受两种载荷影响,一种是外部载荷[5],包括重力、气动力等外部作用力;第二种是分离体之间产生的相互作用力,主要为在分离过程中存在的相互约束力,以及分离体在分离开始时产生的负压力。
2.1 主发动机推力
在分离机构的模型中,主发动机是一个变推力发动机,其推力作用在箭体上,方向竖直向上穿过质心。在发动机推力偏角不存在偏差的情况下,主发动机的推力Py可以近似地认为:
Py=P(t)
(3)
式中:P(t)为发动机推力的时间函数。
2.2 分离火箭推力
在分离机构的模型中,整流罩的分离推力由安装在其内表面的10个分离火箭提供,分离火箭沿圆周分布,其中1~5号分离火箭与6~10号分离火箭呈中心对称安装,如图4所示。分离开始后,1~10号分离火箭同时启动,将整流罩推离下面箭体。当整流罩拔出一定的距离后,6~10号分离火箭停止作用,1~5号分离火箭将整流罩侧向推出。

图4 分离推力分布俯视图
分离火箭在各方向上的推力FLi(i=1,2,…,10)为:
(4)
2.3 气动力载荷
在分离机构的模型中,气动力[6]分别作用在整流罩和下面箭体的质心上。其中气动力Qt为:
(5)
气动力矩Mqt为:

(6)
式中:Qx为x方向气动力;CA为轴向力系数;DA为摩擦阻力系数;St为气动横截面积;Qy为y方向气动力;Qz为z方向气动力;CN为法向力系数;CZ为侧向力系数;qt为来流的动压;Mqx为绕x方向气动力矩;Mqy为绕y方向气动力矩;Mqz为绕z方向气动力矩;lt为t时刻的气动力臂长度;Cmx为滚转力矩系数;Cmy为偏航力矩系数;Cmz俯仰力矩系数;ΔXt为压力中心变化系数;ΔXcmt为质心变化系数。
2.4 分插拔脱力
在分离过程中,分离体之间存在分离插头的连接作用,因此会产生拔脱力。由于在分离平面内的作用力较小,因此只考虑沿分离体纵向的分量,且沿着圆周方向受力均匀,不产生分插拔脱力矩。分插拔脱力根据分离相对距离来判定,当分离距离处在插头松弛长度范围内,不会产生力的作用,当分离距离大于松弛长度,小于拔脱长度,则会产生相应的拉力,力的大小与插头的具体形式有关,当分离距离大于拔脱长度时,力的作用归零[7]。为计算方便,设该力在作用时间内为定值,大小为CT。本分离机构中有3对分离插头,因此在分离体坐标系下分插拔脱力载荷可以表示为:
(7)
式中:CTi为第i个拔脱力矢量;CTi为第i个拔脱力沿竖直(y)方向大小,i=1,2,3。
2.5 分离负压作用力
在分离过程中,分离体之间会产生负压作用力,作用点在分离面几何中心。整流罩受到的负压力FFYU方向竖直向下,下面箭体所受负压力FFYD方向竖直向上,负压力载荷为:
(8)
式中:FFYUy为整流罩受到的竖直方向负压力;FFYDy为箭体受到的竖直方向负压力;FFY(t)为竖直方向负压力随时间变化情况。
3 仿真结果分析
在ADAMS[8]中对分离机构模型进行动力学仿真,创建简单的脚步仿真,终止时间为0.6 s,步长为1 000。
3.1 分离间隙曲线
通过动力学计算与仿真过程,可以得到整流罩和下面箭体的间隙随时间变化曲线,如图5所示。
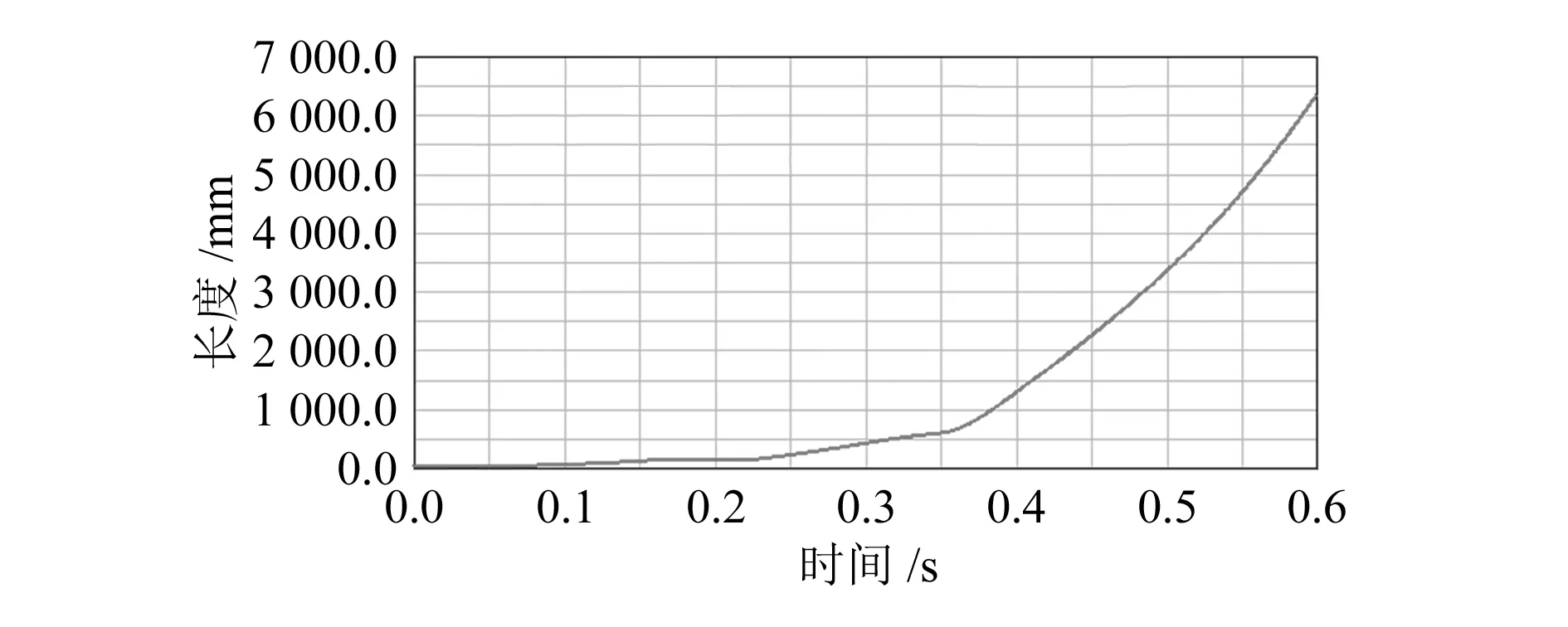
图5 整流罩和箭体间隙随时间变化曲线
从图中可以看出,整流罩和下面箭体之间的最小间隙始终大于零,且随着时间的推移,间隙不断增大。在0.3 s后,间隙增大加快,说明整流罩和下面箭体顺利分离,没有发生接触碰撞等情况。
3.2 分离机构速度曲线
分离机构分离过程中整流罩和箭体的速度曲线如图6 所示。

图6 整流罩与箭体速度曲线
从图中可以看出,在0.3 s之前,整流罩与箭体只存在沿Y轴方向的速度,速度从5 m/s开始增大,而且明显能看出整流罩的速度增长更快。在0.3 s之后,整流罩开始出现沿X轴和Z轴的速度,沿Y轴速度变化不大。整流罩在0.3 s之前与箭体逐渐拉开了距离,有了侧向移动。
分离过程中整流罩和箭体的角速度曲线如图7所示。
从图7可以看出,在分离过程中,下面箭体的角速度非常小,相比整流罩可以忽略不计。整流罩在0.3 s之后,绕X轴和Z轴的角速度从0开始增大,且绕X轴的角速度增长更快,说明整流罩的姿态角变化主要是绕X轴旋转。

图7 整流罩与箭体角速度曲线
3.3 分离火箭推力曲线
1~5号分离火箭推力和6~10号分离火箭推力函数相同,选出比较有代表性的1号和6号火箭推力进行比较,如图8所示。
从图8可以得到,分离火箭在0.035 s时启动,在0.300 s之前,1号火箭X轴向分力为3 723 N,Y轴向分力为12 332 N,Z轴向分力为5 733 N;6号分离火箭X轴向分力为-3 723 N,Y轴向分力为12 332 N,Z轴向分力为-5 733 N。1号和6号火箭推力大小相等,X和Z轴方向相反,Y轴方向相同。0.300 s后,6号火箭推力变为0,1号火箭各个方向推力开始变化,合力不变,说明整流罩的姿态角开始变化。

图8 分离火箭推力曲线
3.4 气动力曲线
整流罩与下面箭体所受的气动力如图9所示。

图9 整流罩与箭体气动力曲线
由图9可以得到,整流罩Y轴初始气动力为-99 N,且在分离过程中逐渐增大;沿X轴、Z轴的气动力和各个方向的气动力矩在分离初始阶段始终为0。在0.35 s之后,各个方向的气动力均开始增大。下面箭体沿Y轴方向初始气动力为-100 N,且在分离过程中数值逐渐增大。沿X轴方向气动力始终比较小,可忽略不计;沿Z轴气动力在分离前期有较小的波动,但数值不大。总体来说,整流罩和箭体受到的气动力都不大。
整流罩与箭体所受的气动力矩如图10所示。

图10 整流罩与箭体气动力矩曲线
由图10可知,整流罩各个方向的气动力矩在分离初始阶段始终为0,在0.35 s后,气动力矩开始明显增大。箭体绕Y轴气动力矩始终为0;绕X轴气动力矩从15 N·m增大到25 N·m,分离前期有波动;绕Z轴气动力矩从-15 N·m增大到-25 N·m。总体来说在分离过程中整流罩和箭体的气动力矩都相对较小,对分离影响不大。
3.5 分插拔脱力曲线
整流罩与下面箭体所受的分插拔脱力曲线如图11所示。

图11 分插拔脱力曲线
由图11可以看出,在分离前期,即分离距离在拔脱长度内时,分插拔脱力大小在100 N和-100 N之间跳跃。说明整流罩和下面箭体受到的分插拔脱力大小相等,方向不稳定但是始终反向。
3.6 分离负压力曲线
整流罩与下面箭体所受的分离负压力曲线如图12所示。
由图12可以看出,在分离开始后,负压力增大到2 000 N又减小到0,在0.3 s整流罩开始侧翻后,负压力又开始增大,说明分离机构在分离状态发生改变时负压力会增大,状态稳定后会减小,且在整个分离阶段整流罩和下面箭体受到的负压力大小相等,方向相反。

图12 分离负压力曲线
4 结论
本文利用多体系统动力学软件建立了一种火箭分离机构的动力学模型,对该模型进行了载荷分析以及动力学仿真,通过分析仿真结果得到以下结论:
1)应用ADAMS进行动力学仿真,可以简化分离机构动力学建模的过程,能更直观地查看动力学仿真结果,更方便进行结果后处理。
2)分离机构在分离过程中分离平稳,整流罩与下面箭体的间隙始终大于零,没有发生接触,实现了整流罩从下面箭体纵向拔出然后被侧向推离的分离目标。
3)在分离过程中,分离体受到的气动力、负压力和插销力等载荷都相对较小,对分离的影响不大。分离火箭推力的变化能直接影响分离机构在分离过程中的速度和姿态变化,对分离机构的顺利分离有决定性作用。
