基于改进PSO-RBF的冗余机械臂逆运动学求解

张淑珍，甄晶博，李春玲，朱红光

(兰州理工大学机电工程学院，甘肃 兰州 730050)

在生产操作中，机械臂关节空间的自由度大于任务操作空间所需自由度时为冗余机械臂，如此末端操作器才能够到达空间中的任意位置，并做出满足工作需求的任意姿势[1]。机械臂的冗余特性可以使其实现力矩优化、避奇异、避障、容错等功能，因此成为当前研究的热点[2]。冗余机械臂逆解存在多解性，需要对其施加额外的约束才能进行逆解优化[3]。同时，冗余机械臂的逆运动学方程是强耦合的非线性方程组，其逆运动学求解较为困难[4-5]。而人工神经网络对非线性方程组有着很好的逼近能力，其中RBF(radial basis function，径向基函数)神经网络是应用较为广泛的神经网络[6-7]。

冗余机械臂的自运动特性可以改善其运动学与动力学性能，如避障、容错等，但是冗余机械臂的逆运动学方程组利用传统方法求解较为困难。罗小平等[8]提出了一种基于关节最佳柔顺性的优化准则，利用模糊RBF神经网络求解平面3R冗余机械臂的运动学逆解，效果较好。付西光等[9]提出了一种基于正交最小二乘法的RBF神经网络算法，对7R扫查机器人逆运动学进行了求解，速度较快，但并未充分利用其冗余性。欧群文等[10]提出了一种基于加权最小二乘法的最佳柔顺性准则，利用遗传算法求出全局最优解，将得到的样本数据作为RBF神经网络的输入，通过训练得到冗余机械臂任意位姿的逆解。

本文针对7轴串联仿人机械臂，利用D-H法建立机械臂的运动学方程，在基于关节最佳柔顺性的基础上，利用改进惯性权重与学习因子的PSO(partical swarm optimization, 粒子群优化)算法，建立求解7轴机械臂的全局最优解模型。由此得到训练神经网络的数据样本，再利用RBF神经网络进行训练，从而获得冗余机械臂运动学逆解。同时，利用MATLAB软件进行仿真实验，验证该方法在冗余机械臂逆运动学求解中的有效性。

1 运动学方程的建立

1.1 建立机械臂坐标系

本文所研究的7轴串联仿人机械臂由3个自由度的肩关节、3个自由度的腕关节与1个自由度的肘关节组成，其尺寸如图1所示。根据D-H方法，对机械臂建立D-H坐标系模型，见表1。表中：αi为连杆扭转角，ai为连杆长度，di为连杆偏移量，θi为关节角变量，其中i为连杆编号，i=1,2,…,7。

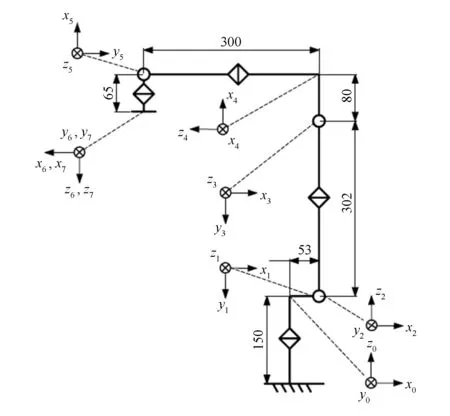
图1 7轴机械臂连杆坐标模型

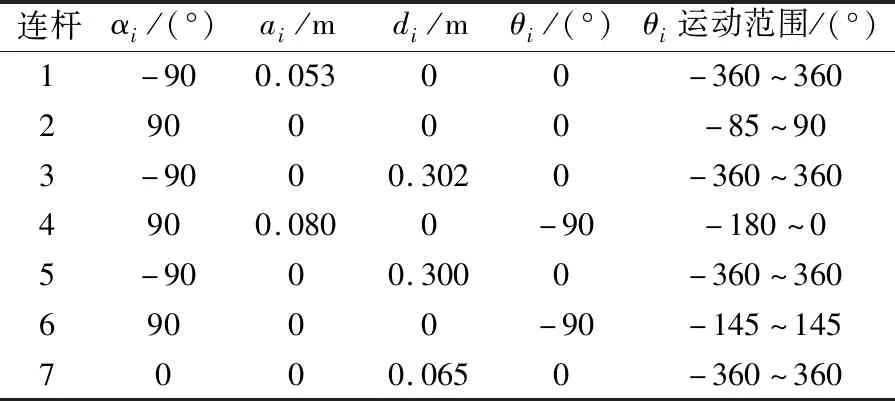
表1 7轴机械臂的D-H参数

1.2 运动学分析

根据表1中的7轴机械臂的D-H参数，利用式(1)计算出机械臂相邻关节的变换矩阵i-1Ti。

(1)

式中：Cθi=cosθi，Sθi=sinθi，Cαi=cosαi，Sαi=sinαi。根据各关节齐次变换矩阵i-1Ti通过式(2)计算出机械臂的运动学正解。

0T7=0T11T22T33T44T55T66T7=

(2)

式中：0T7为关节1到7变换矩阵；nx,ny,nz为n轴方向余弦；ox,oy,oz为o轴方向余弦；ax,ay,az为a轴方向余弦；Px,Py,Pz为位置坐标。

1.3 欧拉变换

机械臂末端姿态采用欧拉角表示。利用式(2)将旋转矩阵表示的姿态转化为欧拉角表示的姿态矩阵。将机械臂的姿态矩阵按照Z-Y-Z轴旋转顺序进行欧拉变换得到欧拉角α，β，γ，欧拉变换可以将12个变量的相关输入转化为6个变量的独立输入[11]。变换公式为：

α=atan2(ay,ax)

(3)

β=atan2(axcosα+aysinα,az)

(4)

γ=atan2(nycosα-nxsinα,oycosα-oxsinα)

(5)

P=(α,β,γ,Px,Py,Pz)

(6)

式中：P为位姿矢量。

2 PSO算法优化

2.1 PSO算法原理

PSO算法是一种模拟鸟群觅食机制的算法，通过搜索、更新当前最优位置与速度来找到全局最优解。PSO算法的粒子具有记忆的特性，通过学习使下一代解能够从上一代解中继承信息，从而能在短时间内找到最优解。PSO算法具有运算简便、收敛速度快等优点，得到了广泛应用。

PSO算法首先初始化n个随机粒子，每个粒子具有不同的位置Xi(i=1,2,…,n)与不同的适应度值fitness(Xi)。在每次循环中，粒子都会更新个体极值pbest和全局极值gbest[12]。当找到两个最优值时，粒子根据式(7)、(8)更新速度vi与位置Xi。

(7)

(8)

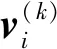
(9)

式中：vmin和vmax分别为粒子速度最小值和最大值；Xmin和Xmax分别为粒子所能到达位置的最小值和最大值。

2.2 PSO惯性权重与学习因子改进

在PSO优化算法中，只有个体极值pbest与全局极值gbest将信息传递给其他的粒子，这使得算法在搜索更新时会跟随当前最优的粒子,从而导致迭代陷入局部最优值，出现早熟收敛或停滞现象。鉴于此，本文提出改进的PSO算法对标准PSO算法的惯性权重与学习因子进行了优化，在提高算法精度的同时，避免了PSO算法的局部最优问题，图2为改进的PSO算法流程。

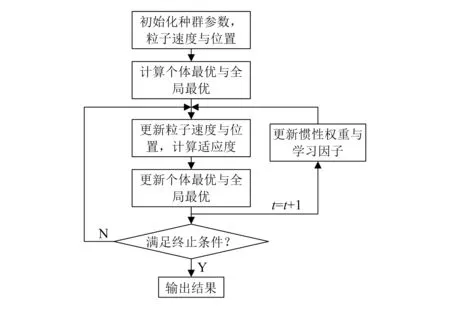
图2 改进的PSO算法流程

2.2.1惯性权重的改进

惯性权重ω决定粒子的搜索能力：较大的惯性权重可以使迭代跳出局部最优，有利于全局搜索；而较小的惯性权重则有利于对局部区域进行搜索，有利于算法收敛[13]。标准PSO算法中惯性权重ω一般取1左右的值，本文采用一种非线性的惯性权重系数，惯性权重ω随着迭代次数的增加而减小，同时兼顾全局与局部搜索效率。

(10)

式中：favg为平均适应度值；fmin为最小适应度值；ωmax=0.9，ωmin=0.2。

2.2.2学习因子的改进

学习因子c1反映的是粒子向自身历史最佳位置逼近的趋势；学习因子c2反映的是粒子向全局历史最佳位置逼近的趋势[14]。标准PSO算法中学习因子一般取2左右的固定值，本文采用一种随惯性权重ω变化的自适应学习因子，如式(11)所示。在搜索前期，c1取较大值，c2取较小值，以增强全局搜索能力；在搜索后期，c1取较小值，c2取较大值，以增强局部搜索能力。

(11)

2.3 适应度函数的建立

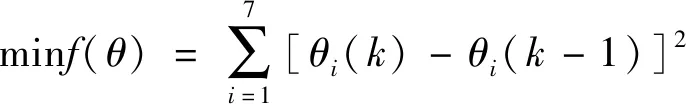
(12)

式中：[θi(k)-θi(k-1)](k=1, 2, …)为机械臂关节i的关节角与自身前一时刻关节角的差值。本文先将7自由度机械臂运动学模型转化为6输入7输出的映射模型，再利用式(13)中的外点法惩罚函数将机械臂的有约束问题转化为无约束问题。

h(α,β,γ,Px,Py,Pz)=(α-α0)2+(β-β0)2+(γ-γ0)2+(Px-Px0)2+(Py-Py0)2+(Pz-Pz0)2

(13)

Fitness=minf(θ)+Mk×h(α,β,γ,Px,Py,Pz)

(14)

式中：f(θ)为目标函数；h(α,β,γ,Px,Py,Pz)为惩罚函数；Mk(k=1,2,…)为随迭代次数的增加而增加的惩罚因子；Fitness为机械臂PSO算法的适应度函数；α0,β0,γ0为初始角度。

3 RBF神经网络原理

RBF神经网络能够逼近任意的非线性函数，收敛速度快，具有良好的逼近精度与泛化能力。此外，RBF神经网络还解决了BP神经网络易陷入局部最小值的问题。本文将α,β,γ,Px,Py,Pz作为RBF神经网络的输入变量，θi(i=1,2,…,7)作为RBF神经网络的输出变量。

RBF网络是三层前馈网络，由输入层、隐藏层、输出层组成[15]。网络建立了从系统输入X(x1,x2,…,xm)到系统输出Y(y1,y2,…,yk)的映射关系，其中隐藏层的节点数为n。RBF网络通常采用高斯函数作为传递函数，利用式(15)建立从输入层到隐藏层的非线性映射，再利用式(16)建立从隐藏层到输出层的线性映射。如果神经元的输入离径向基函数中心越远，那么神经元的激活程度就越低，因此RBF神经网络具有局部映射的特性。随着误差传递的不断进行，RBF网络输出响应的误差越来越小，直到满足训练设置条件为止，该过程如图3所示。

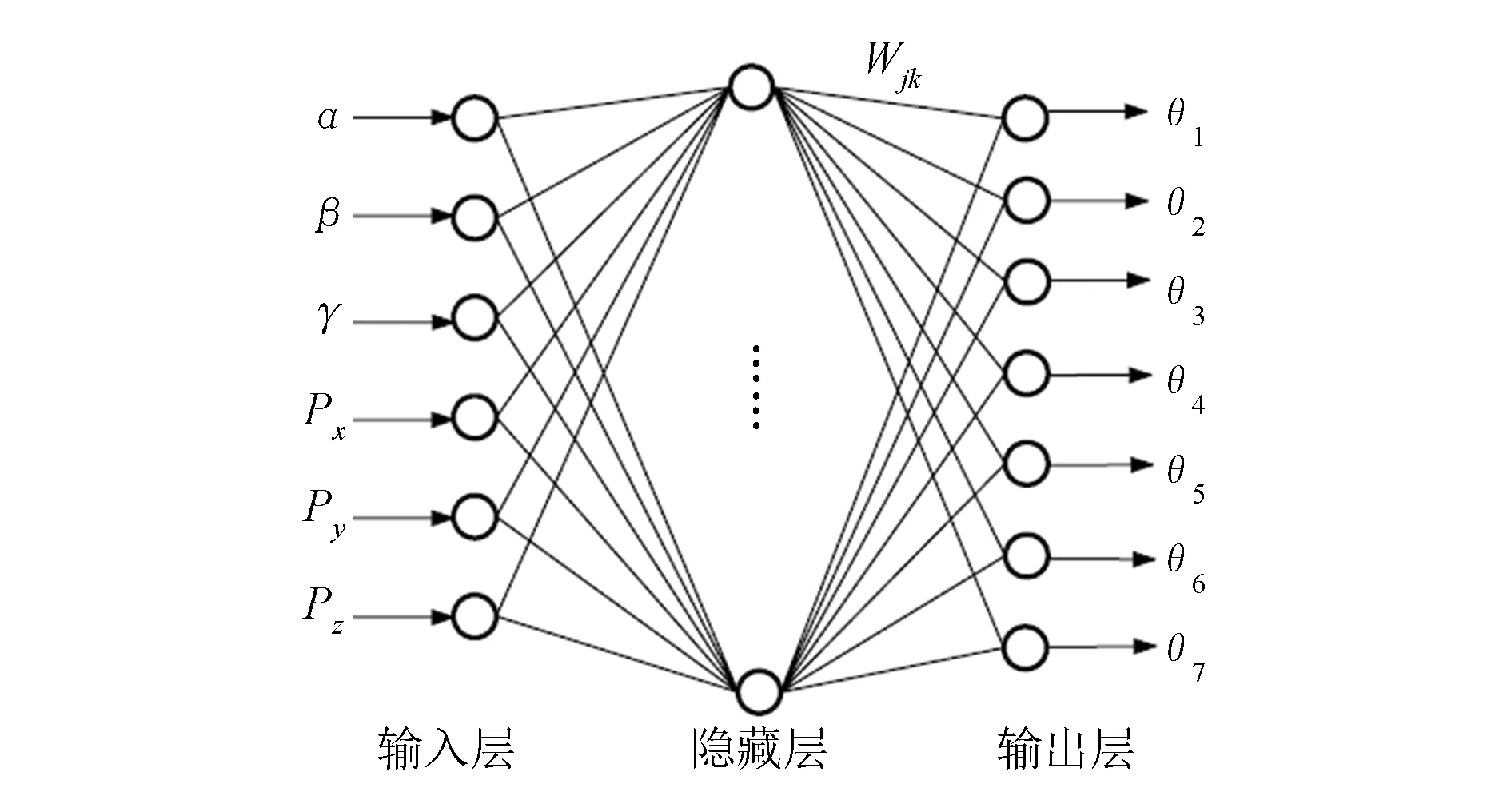
图3 机械臂RBF神经网络模型

(15)

(16)

式中：Rj(x)为隐藏层第j个神经元的传递函数；x为网络的输入；cj与σj分别为径向基函数的数据中心与宽度；Yk为RBF神经网络的输出；Wjk为隐藏层第j个神经元到输出层第k个神经元的连接权值。

4 仿真实验

为证明算法的有效性，在MATLAB 2016a的环境下建立了PSO-RBF网络模型。

4.1 PSO优化

本文中标准PSO算法与改进PSO算法的种群规模定为20，最大迭代次数为200。其中，标准PSO算法的惯性权重ω=0.9，学习因子c1=c2=1.5，改进PSO算法的惯性权重与学习因子分别采用式(10)与式(11)计算。

首先选择单个数据工作空间的位姿进行验算，笛卡尔空间初始点的位姿矩阵P0如下所示：

经过PSO算法优化点的位姿矩阵的各关节逆解θ0为：

θ0=[0.050 0 -0.358 3 -0.203 2 -1.363 9 0.314 6 -1.405 5 -0.289 4]

代入正运动学的机械臂位姿向量p0为：

p0=[-1.827 0 2.900 6 -1.927 8 -0.150 9 0.033 6 -0.310 1]

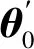
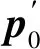
图4 PSO算法与改进PSO算法迭代曲线

随机选取工作空间10组数据，用标准PSO算法与改进PSO算法求得逆解θi(i=1,2,…,7)后，代入回正运动学方程，其位姿向量pi(i=1,2,…,10)的均方差见表2，由表可见，改进PSO算法的均方差0.003 6小于标准PSO算法的均方差0.012 9。

表2 标准PSO算法与改进PSO算法均方差

4.2 RBF网络仿真

取笛卡尔空间中直线上均匀分布的点P1(-0.348 5, 0.051 8,0.257 6)至点P100(-0.255 0,-0.101 2,0.272 6)，经改进PSO算法优化后的数据作为RBF网络的样本。从点P1到点P100中随机选取10组数据样本作为RBF网络的测试集，其余90组数据样本作为RBF网络的训练集。在MATLAB中，RBF神经网络的参数err_goal设为0.01，径向基函数的spread设为3，最大神经元个数MN设为200。利用newrb函数建立RBF网络的模型，并对90组数据样本进行训练，当网络达到设定的误差值时，终止训练并对测试集进行仿真。

利用PSO算法计算出7轴机械臂的运动学逆解，结果见表3。再利用RBF神经网络对训练集进行训练，得出测试集结果。将PSO算法优化的逆解代入机械臂正运动学方程，与RBF神经网络测试集输出作对比(表4)。由此可见，RBF神经网络测试集输出的三维坐标ox,oy,oz的位置精度已能够满足生产需要，验证了本研究的可行性。

表3 PSO算法求运动学逆解结果 rad

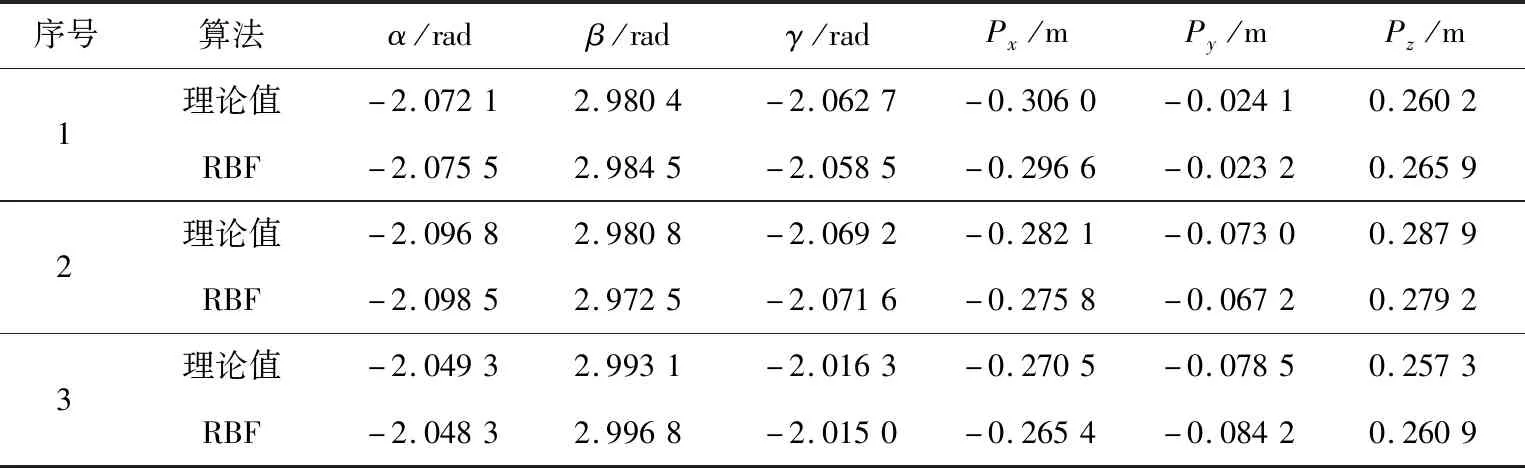
表4 RBF网络训练末端位姿结果

5 结束语

本文利用基于最佳柔顺性的惩罚函数法建立冗余机械臂的适应度函数，解决了冗余机械臂逆解的多解性问题，并得到了冗余机械臂各个位姿唯一的逆解。在此基础上，利用PSO算法对其逆解进行了优化，通过对惯性权重与学习因子的改进，使得PSO算法具有更高的计算精度，并最终获得了机械臂运动学的样本数据。此外，本文还利用RBF神经网络对优化的样本数据进行了训练，得到了稳定状态的神经网络。MATALB仿真结果表明本文提出的方法是有效的，该方法可以作为求冗余机械臂运动学逆解的有效方法。