用于非精确图匹配的改进GCN模型*
2020-08-12李昌华崔李扬李智杰
李昌华,崔李扬,李智杰
西安建筑科技大学 信息与控制工程学院,西安 710055
1 引言
图是一种丰富的表示形式,可以描述现实世界中复杂的结构数据,如化合物集合、蛋白质结构、社交网络等。随着深度学习技术应用于许多领域,并且较传统方法有明显优势,利用神经网络对拓扑结构特征的学习和查询为高效的图匹配算法带来了应用需求。
图匹配方法可以分为两类,精确图匹配和非精确图匹配。精确图匹配要求被匹配的对象之间要严格对应[1]。然而,这种匹配算法的强约束条件对于实际应用来说过于严格,并被证明是NP完全问题。相对于精确图匹配,非精确图匹配方法允许在相似模型下有一定的容错,即使被匹配的图在结构上有一定的差异,也能进行匹配,这使得非精确图匹配受到研究者们的重视。虽然目前已经有很多非精确图匹配问题的研究,但是现有算法的识别率、有效性仍不能满足要求。
卷积神经网络(convolutional neural networks,CNN)作为一种深度监督学习框架,在计算机视觉[2]、语音识别[3]、博弈[4]等领域都表现出了优异的性能。对于图像、视频和声音等数据,它们都具有固定大小的邻域,因此CNN 中的卷积、池化等操作是有意义的。然而,图是一种结构化数据类型,没有固定的邻域,传统的CNN不能直接作用于图。而为了将CNN应用于图结构数据,研究者们提出了多种方法[5-9]。这些方法可以分为两类:基于空间的方法和基于谱的方法。基于空间的方法是利用图的空间邻域信息进行卷积运算。基于谱的方法通常使用拉普拉斯变换对结构图进行变换,然后使用特征向量作为卷积算子。文献[10]提出了一个学习图的CNN 框架,通过使用图标记程序来构建一个感受野。上述方法虽然在一定程度上解决了将CNN 应用于图的问题,但是依然存在对图结构本身挖掘不够充分的问题。
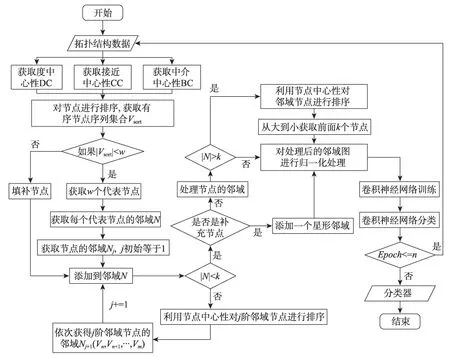
为了解决这些局限性,本文通过引入图卷积神经网络(graph convolutional network,GCN),改进从拓扑结构数据映射为网格结构数据作为卷积神经网络输入的过程,主要工作如下:首先通过社交网络分析(social network analysis,SNA)[11]中三种衡量网络节点中心度的方法对比并获取最优有序节点序列,选取代表节点;其次针对节点邻域大小不满足感受野阈值的情况,对节点邻域进行中心度排序,依次获取邻域节点的一阶邻域,直到邻域大小满足感受野阈值。改进的GCN 在把拓扑结构处理为网格结构时,其节点邻域图能最大限度表示原图结构,之后对邻域进行归一化处理,结合卷积神经网络模型对图进行训练与识别。图1展示了该模型的算法流程,其中左边虚框为训练过程,右边虚框为测试过程,实验表明该方法可以更有效地保留数据的拓扑结构信息,提高非精确图匹配精度。
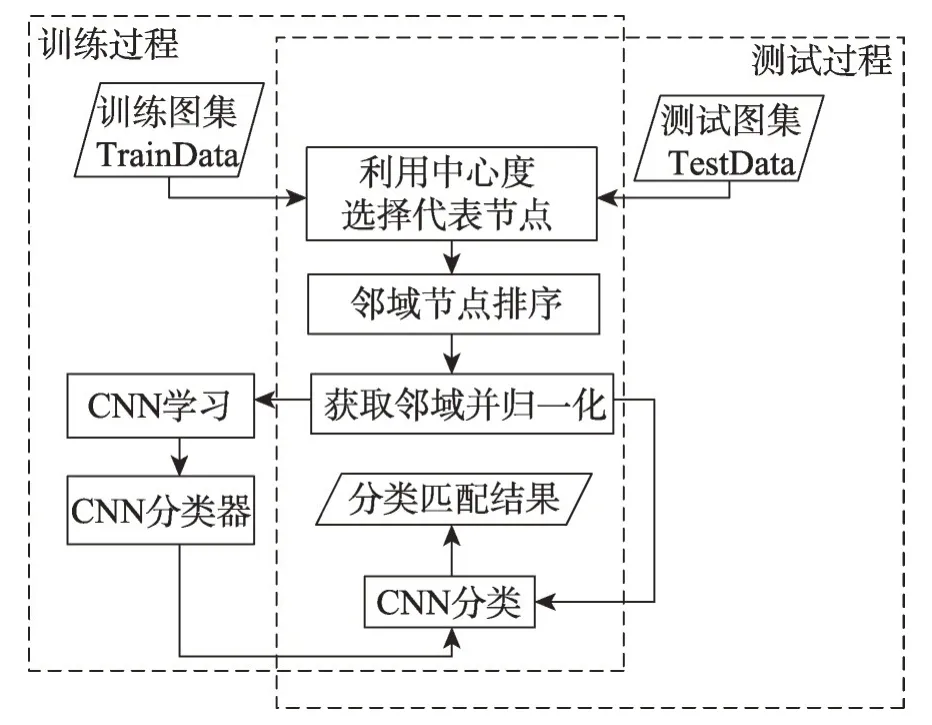
Fig.1 Algorithm flow of model图1 模型算法流程
2 GCN的相关工作
在深度学习领域,用于处理图这种非欧几里德数据的CNN称之为图卷积神经网络(GCN)。这种方法的做法通常是将标准的CNN应用于图数据特征学习,相对于在图像上的卷积[12],在图上的卷积需要考虑其空间结构。文献[13]提出一种图神经网络框架,文献[14]对其进行了简化,利用循环神经网络将每个节点嵌入到欧氏空间中,并将这些嵌入作为节点或图的分类与回归特征,然而这种算法的引入参数较多,效率比较低。为了减少学习参数的数量,文献[15]引入了构建局部感受野的概念。这种方法的思想是将基于相似性度量的特性组合在一起,例如在两个连续层之间选择有限数量的连接。虽然该模型利用局部性假设减少了参数的数量,但并没有试图利用任何平稳性,即没有权值共享策略。文献[16]将这一思想用于图CNN的空间表示(空间规划)。他们使用加权图来定义局部邻域,并为池操作计算图的多尺度聚类。然而,在空间结构中诱导权重共享是具有挑战性的,因为当缺少特定于问题的排序(空间、时间或其他)时,需要选择和排序邻域。文献[17]提出了一种从数据中学习图形结构的策略,并将该模型应用于图像识别、文本分类和生物信息学。然而,由于需要与图的傅里叶基U相乘,这种方法并没有扩大。
文献[10]提出了一种获取图数据的局部接受域并应用于CNN 的方法,该方法可以得到一个标准CNN可以处理的一维数据单元,文献[18]是在该方法的基础上添加了一个预处理卷积层,文献[19]是在卷积之前对数据进行了排序,这些方法虽然在一定程度上优化了文献[10]中的方法,然而它们都局限在对卷积的处理,并没有考虑到把拓扑结构映射到网格结构的过程中对数据的最优表示,因此无法保证获取的节点邻域能最大化表示节点的领域特征。本文的工作充分利用其优点,并且在关键节点选择与获取节点邻域上进行改进,使节点邻域能最大化表示拓扑图结构,进而利用改进的GCN 模型处理非精确图匹配问题。
3 改进的GCN模型
本章描述了用于图匹配的改进图卷积神经网络模型。首先,图的分类匹配问题可以归结如下。
标记图可以表示为G=(V,E,α),V是顶点集合,E=V×V是边的集合,α是顶点标记函数,α:V→∑V,其中∑V是节点标签的内容。示例:其中x是图集,xi∈x,yi∈y={+1,-1}是目标标签,图分类匹配问题可以映射为f:x→y的函数求解问题。
因此把CNN 应用于拓扑结构,首先需要对拓扑结构数据进行处理,如何保证选取的关键节点具有代表性,以及在获取节点邻域过程中保证邻域节点能较完整表示图的结构是一些亟待解决的关键问题。为解决这些问题,本文提出一种新的算法模型,如图2 所示。首先使用三种求取网络节点中心度的方法对节点进行度量并排序,选取关键节点,然后利用中心度对邻域节点排序并依次获取节点邻域。模型主要包括:
(1)代表节点选择:通过SNA中三种网络节点中心度度量方式计算节点中心度,获取节点有序序列,通过对比来选取最优代表节点。
(2)邻域节点排序(neighbour node sort,NNS):对邻域节点进行中心度排序,按中心度大小依次进行邻域节点的选取。
(3)邻域节点归一化:把节点邻域规范化为网格结构,作为卷积神经网络的输入。
(4)特征学习:归一化的图结构数据经过两层卷积以及全连接层进行特征学习。
在图2的模型结构中,其输入是数据集MUTAG[20]中的任意一个图,首先节点经过中心度大小排序选出代表节点,图示给出三个代表节点的例子,其次经过邻域节点排序,获得节点邻域,归一化之后获得网格图,作为卷积神经网络的输入。
3.1 代表节点选择

Fig.2 Improved model structure图2 改进的模型结构
本文使用三种网络节点中心度度量方法获取代表节点。中心度(centrality)[11]是SNA 中常用的一个概念,用以表达社交网络中一个节点在整个网络中所在中心的程度,这个程度用数字来表示就被称作中心度。本文使用的测定节点中心度的方法有度中心度(degree centrality,DC)[11]、接近中心度(closeness centrality,CC)[21]、中介中心度(betweenness centrality,BC)[22]。
(1)DC:节点v的度,对于无向图来说是连接该节点的边数,对于有向图,存在出度与入度。出度为从节点v出发的有向边,入度为指向节点v的有向边。本文主要讨论无向图,因此节点v的度中心度:

(2)CC:如果一个节点与许多其他节点接近,那么该节点处于网络中心位置,这种度量方式称之为接近中心度:

设图G(V,E,α),其中V表示节点集合,E表示边的集合,则上式|V|表示节点的个数,dvi表示节点v与节点i之间的距离。接近中心度体现的是一个节点与其他节点的邻近程度。
(3)BC:中介中心度是计算经过一个点的最短路径的数量。经过一个点的最短路径数量越多,就说明它的中介中心度越高。中介中心度表示为:

其中,σst(v)表示经过节点v,s→t的最短路径数,σst表示s→t的最短路径数。
中心度的计算决定了代表性节点的选择,从而对训练结果有着直接的影响,因此一个好的中心度选取算法的重要性不言而喻。利用中心度获取代表节点序列分为两步,首先根据中心度算法计算节点的中心度并以此排序,其次选取w个代表节点序列。其算法流程如下:


代表节点的选择是算法2 通过调用算法1 计算而来,首先对于一个图G(V,E,α),作为算法2 的输入Selectnode(G),获取其节点V,并通过算法1Getcentra-lity 获取每个节点的中心度CV={Cv:V},并按中心度Cv大小对节点排序,获取有序序列Vsort,并从Vsort中获取前w个节点,对|Vsort|不满足w大小补充零点vzero,最终得到代表节点序列Vkey。
3.2 邻域节点排序
对于一个图G=(V,E,α),设n是图中节点的个数,m是边缘个数。那么图可以用一个n×n邻接矩阵A表示,如果节点vi到节点vj之间有边存在,令Ai,j=1,否则Ai,j=0。N1(v) 是节点v的一阶邻域,即N1(v)中的节点都与节点v相邻。
CNN 对图像进行卷积操作,每个像素都有相同的邻域大小,因此节点邻域的大小要与第一层卷积的感受野大小相同。本文通过对邻域节点排序,按照邻域节点中心度大小依次获取邻域节点。邻域可以表示为:

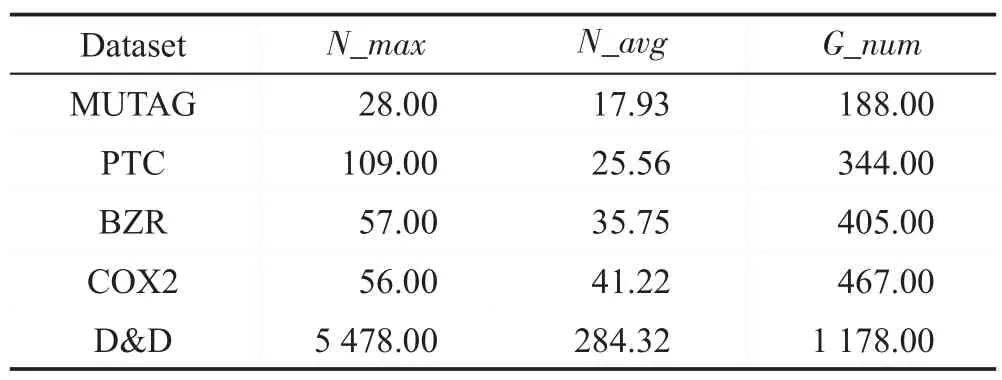
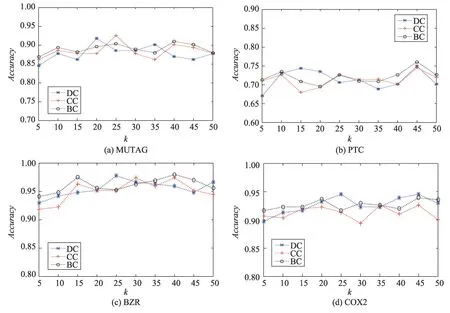
其中,j是图的节点数目并且j∈R,j 当j=1 时,N1(v)表示与节点v直接相邻的节点集合。在本文中获取关键节点的邻域过程:设邻域大小为k,即集合N(v)的长度len需要等于k。在实际的算法过程中,首先获取节点v的1 阶邻域,可能会存在len>k与len 结合式(4)和式(5)来说明邻域节点排序获取节点邻域的过程。式(6)表示与节点v相邻节点vi到vm的集合,即1 阶邻域,1 阶邻域通过式(7)的SN(v)函数之后获得有序的邻域节点,按中心度大小依次获取2阶邻域,其2阶邻域表示为式(8),在不满足预设邻域k时,以式(6)~式(8)的计算公式获取节点v的Nj邻域,那么关键节点的邻域N(v)表示节点v的1到j阶邻域的并集,如式(9)所表示,即式(4)的邻域。 在上述式子中,C(v)是节点中心度函数,sort(∙)是按照节点中心度对节点进行排序,SN(v)是通过网络中心度获取的序列集合。 上述过程描述为NNS 算法,则利用NNS 获取邻域的算法步骤如下: 在图2 中所示的邻域节点预设长度为k=5,在获取N(1) 之后邻域大小小于5,因此继续获取为N(2),此时采用了邻域节点排序为1的节点邻域。为了体现这个过程,图3 展示了一个k=8 的例子。其中在获取N(1)后邻域小于8,经过NNS算法排序后依次获取节点的2阶邻域。 Fig.3 Neighborhood node sort图3 邻域节点排序 本文选取的用于特征学习的CNN 拥有两层卷积,一个Flatten 层,为防止过拟合使用了DropOut 方法,其模型如图4所示,其中第一层卷积,卷积窗口大小为k,步长为k,输出Dense 层使用的激活函数为Sigmoid。 在卷积层Conv1 用一组过滤器在节点属性图上进行滑动,提取图上关键节点以及邻域的特征。形式上,在向前传递期间,过滤器滑过节点及其邻域,计算过滤器的每个值与输入属性图之间的点积。过滤器的输出计算如下: Fig.4 CNN architecture图4 卷积神经网络结构 目标函数经过激活函数Sigmoid 之后得到下一层神经元的激活值,其中a0表示的是输入层中的神经元的值,本文的a0=G(attr)是一个节点属性矩阵,其长度大小等于关键节点个数w与其邻域大小k的乘积,维度与节点的属性值向量一致。其中l表示行,m表示列,s表示Stride 即卷积窗口每次移动的大小,l′a表示节点属性向量的维度大小。 利用交叉熵损失函数来更新权重,其损失函数为: 其中,θ是模型的参数;yi是图i的真实标签;y′i是输出网络模型的输出。 另外为防止训练过程过早结束,使用RMSProp(root mean square prop)梯度下降算法,利用自适应学习率对权重与偏向进行更新,相关公式如下: 式(13)、式(14)中η为学习率,ε是防止分母为0的无穷小量,是参数θ的梯度平方求数学期望。 图5 给出了一个原始训练集图数据在模型中训练的流程图。利用CNN训练数据获取分类器: 初始化:加载原始图集G,训练次数n,感受野大小k,代表节点个数w。 输入:图集G。 带入式(10)y=σ(b+w×a0)训练模型并利用式(12)~式(15)更新权重 Fig.5 Data training specific process图5 数据训练具体流程 选取带有标签的数据集对模型进行训练,图5流程的关键步骤如下: 步骤1初始化训练次数Epoch,感受野大小k,w为图集节点的均值。 步骤2输入训练所使用的数据集G。 步骤3根据算法2获取关键节点序列Vkey。 步骤4对于Vkey中的每一个节点,判断其是否是原图节点,若是则利用NNS算法获取邻域节点,并由这些节点生成子图subgraph,否则添加一个星形图作为子图subgraph。 步骤5对每一个子图进行归一化,获得节点感受野G[N],获取子图节点的属性并reshape 属性矩阵G(attr)大小为k×w与节点属性长度。 步骤6把G(attr)作为卷积神经网络模型的输入对数据进行训练,最后得到模型分类器。 为了验证改进的GCN模型在图上的实际分类结果,在多个基准数据集上进行了测试,并在本部分给出实验结果与分析。 (1)MUTAG[11]:MUTAG 是有188 个硝基化合物的数据集,其中化合物的分类表示该化合物是否对细菌具有诱变作用。 (2)PTC[23]:PTC 由344 种化合物组成,其中化合物的分类表示该化合物是否对老鼠有致癌性。 (3)BZR[24]:BZR 由405 个化学元素组成,分类表示是否对医学中一种酶的抑制有活性。 (4)COX2[24]:COX2是有467个元素的数据集,其分类表示在体外对人体重组酶是否有抑制作用。 (5)D&D[25]:D&D 是有1 178 个蛋白质结构的数据集,其中化合物分类表示是否是酶。 表1 是各个数据集的基本数据,其中N_max表示数据集中拓扑图的最大节点数,N_avg是数据集的平均节点数,G_num表示含有的图数量。 Table 1 Dataset information表1 数据集信息 (1)检验使用DC(degree centrality)、CC(closeness centrality)、BC(betweenness centrality)算法对模型分类的识别率与稳定性的影响程度,其中DC算法在原始GCN 模型方法PATCHY-SAN(patchy select assemble normalize)中所应用。在MUTAG、PTC、BZR、COX2数据集上进行实验,以数据集的平均节点数为选取关键节点的阈值,采用5~50 间隔为5 的不同大小邻域k进行10 组实验,测试邻域大小对算法模型识别率的影响,对比3 种算法的匹配精度,另外对实验结果数据求解方差,通过对数据波动的程度分析来检验算法的稳定性。 (2)在实验结果分析的前提下获取本文最优算法,在MUTAG、PTC、COX2、BZR 以及D&D 数据集上进行实验,每个数据集上进行了10次实验,并与文献[10,26-28]中算法进行对比,验证本文最优算法的识别率。 (3)为体现算法的性能效率时间耗费代价优劣程度,对各算法的时间复杂度进行对比分析。 上述对比实验中所涉及文献方法分为两类: (1)图核算法:SP(shortest-path)核[27]、WL(Weisfeiler-Lehman)子树核[28]。 (2)GCN方法:PATCHY-SAN[10]、LMFGCN(learning molecular fingerprints graph convolution networks)[26]。 其中算法SP与WL为经典的图核方法,PATCHY-SAN方法是本文改进之前GCN模型方法,LMFGCN是一种把图的节点和边缘转化为特征向量进行端到端学习的GCN模型方法。 本文在实验中所选取的卷积参数第一层为16个卷积核,卷积窗口大小为k,步长为k;第二层卷积为8 个卷积核,卷积窗口大小为10,步长为1,全连接的激活函数为Relu,Dropout为0.5,输出中添加的Dense层使用的激活函数为Sigmoid,Epoch的值为10。 4.3.1 DC、CC、BC对比与分析 图6 展示了算法DC、CC、BC 对拓扑结构数据在不同邻域大小下分类匹配的识别率对比。以折线图的方式呈现更能直观地展现在不同数据集上3 种方法对模型分类匹配的识别率影响程度。 数据集MUTAG中图最大节点数28,平均节点数是18,图6(a)是其在3 种算法下的识别率,从图中可以看到CC 算法在邻域k=25 可以达到93%的识别率,算法BC在邻域k=20 识别率取得最大值,然而在邻域大小取其他值时,二者的识别率没有使用BC算法时高。图6(b)是在数据集PTC上的实验,3种算法的识别率在k=45 时均取得最大值,CC与BC算法在10 组实验室中整体的识别率差距不大,算法DC 在k=15 与k=20 时的识别率较其他两种算法较高。图6(c)与图6(d)分别是在数据集BZR与COX2上的实验结果,从图中可以看出分类识别率达到90%以上。k=25 时DC 与BC 算法在两个数据集上的识别率差距都比较大,BZR与COX2数据集中图的最大节点数与平均节点数比较接近,这使得在k的一定阈值内两个数据集实验出来的识别率差距类似,然而当k>30时,BC 算法在数据集BZR 上有较好的体现,对于COX2 则是DC 算法的匹配识别率更高,当k≤20 时较之其他算法,BC 算法在两个数据集上都具有较好的识别率。 整体从识别率折线图的数据上看,4个数据集在k的个别取值均存在离散度较大的点,如果排除这些点,BC算法在各个数据集上的匹配识别率相对较高。 Fig.6 Classification and recognition rates of 3 algorithms图6 3种算法的分类识别率 Fig.7 Variance of experimental data图7 实验数据方差 图7 是在数据集上3 种算法实验结果数据的方差。方差可以衡量一组数据波动大小,方差越小,说明这组数据的波动性比较小;反之,则表明数据波动性大。通过实验结果的数据方差可以确定在不同的k的取值下3种算法的稳定性如何。图7中从左到右依次是在4个数据集上3种算法实验结果方差。对于3 个数据集MUTAG、PTC 与COX2,DC 算法的实验结果数据方差最大,则此算法稳定性在这些数据集上较弱。其次,对于数据集BZR,CC 算法的稳定性比其他算法较弱。另外,在数据集PTC上,CC与BC算法的稳定性相差不大,而3 种算法在数据集COX2上的稳定性都相对较好,然而可以很明显地看到黄色柱形图在4 组方差数据中均处于最低,因此BC 算法的稳定性最好。在3种算法的对比实验中,设置的k均超过了数据集的平均节点数,也就是存在补充节点。在接下来的实验中,为减少引入的节点所带来的误差,本文选取k=10 进行接下来的实验。并且从算法的识别率与稳定性分析来看,BC 算法在3 种算法中最优,因此利用BC算法进行接下来的实验。 由于DC 算法为原始GCN 模型方法PATCHY-SAN 所应用,因此证明BC 算法在3 种算法中最优的同时也证明了BC 算法相对于原始GCN 模型是有效的。 4.3.2 同类方法对比与分析 表2展示的是6种方法在5个数据集上的分类匹配的识别率。其中BCNNS是本文的引入了BC算法与NNS 节点排序算法的方法。而BC 是在没有NNS算法的情况下在各个数据集上的实验,让BC 与BCNNS 进行对比是为体现算法NNS 的有效性。在之前的对比实验中可以得出BC 算法在一定程度上提高了算法的识别率与稳定性,添加了NNS 算法的BCNNS,其在识别率上较之BC算法有了进一步的提升,并且在PTC数据集上有较高的提升,在其他数据集上的识别率也有一定程度的提升,因此NNS 算法的引入是有效的。另外,在数据集D&D 上的实验也是为了验证BC 算法较优的实验结果。本文提出的BCNNS 算法在数据集PTC、COX2、BZR 及D&D 上都有较好的分类匹配识别率,其中在数据集PTC 与COX2 上的分类匹配识别率提升较大。相较于传统的图核SP与WL方法,BCNNS方法在大部分数据集上都有较好的分类匹配率。比较其他两种基于CNN的拓扑图分类匹配算法,BCNNS 算法不仅在分类匹配识别率上有所提升,其在稳定性方面也有优势(在10组实验中,BCNNS算法在数据集上的识别率上下波动的范围较小)。从表2 中可以看到,对于数据集MUTAG,识别率峰值不如PATCHY-SAN 方法,原因是该数据集平均节点数较小,本文提出的邻域节点排序对其拓扑结构数据的影响不是特别大,但是加入了BC 方法的BCNNS 算法在稳定性上有所提升。因此,在大部分数据集上,本文的BCNNS 算法优于现有的图卷积神经网络方法与图核方法。 Table 2 Classification and recognition rates of 6 algorithms on 5 datasets表2 6种方法在5个数据集上的分类识别率 % 4.3.3 算法复杂度对比与分析 BCNNS 算法的各个模块之间是相对独立的,因此构建感受野的过程是高效的并且可并行实现。设N'是图的个数,k是感受野的大小,w是宽度,n为图的顶点个数,m为边的个数。则BCNNS算法在N'个图上计算感受野的最坏时间复杂度为O(N′w(nm+nlb(n)+exp(k))),其中O(nm)是BC算法在一个图上的时间复杂度,O(nlb(n))为NNS 排序算法的时间复杂度,exp(k)是图归一化算法Nauty 计算有n个节点的最坏时间复杂度。 对于GCN模型算法LMFGCN与PATCHY-SAN,前者是解决分子指纹识别问题,其中指纹的深度对应邻域大小w,固定指纹长度对应的是感受野大小k,则LMFGCN算法复杂度为O(N′w(Fk+F2)),其中F为节点与边缘特征,当节点与边缘都存在一个特征时,F=n+m,此时复杂度达到O(N′w((n+m)k+(n+m)2));PATCHY-SAN 算法的时间复杂度为O(N′w(f(n,m)+nlb(n)+exp(k))),其在论文中使用的标记函数为f(n,m),算法复杂度最坏情况为O(n2),当m 本文提出的BCNNS算法具有以下特点: (1)利用中介中心度对节点进行度量,进而使选取的关键节点更具有代表性,这种度量方式可以适用于任意的无向图。 (2)能够使获取的邻域节点最大限度地表示图的局部特征,从而由局部到整体,使CNN有针对性地进行学习。 通过实验证明了算法的有效性,但有待改进的地方在于对邻域进行归一化的过程中,会引入零点,虽然对算法的效率有所提升,但会存在冗余情况。因此下一步的工作将对这一过程进行优化,减少冗余的出现,进一步提高匹配算法的识别率。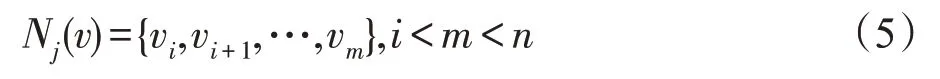
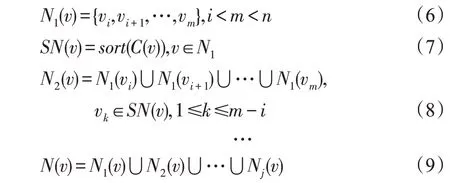


3.3 CNN架构
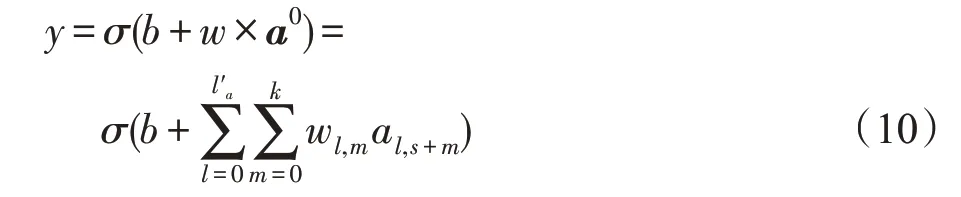
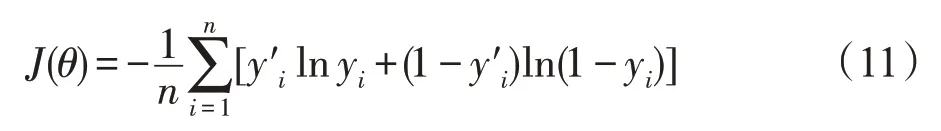




4 实验结果
4.1 数据集
4.2 实验设置
4.3 实验结果


5 结束语
