一种面向不完备信息系统的集对k-means 聚类算法

张春英，高瑞艳，刘凤春，王佳昊，陈 松，冯晓泽，任 静

（1.华北理工大学理学院，唐山，063210；2.华北理工大学迁安学院，唐山，063210；3.河北省数据科学与应用重点实验室，唐山，063210）

引 言

作为一种强大的数据分析工具，聚类在数据挖掘中起着重要作用，广泛应用于异常数据检测[1-2]、生物信息学[3]和网络结构分析[4]等领域。聚类的目的是将相似的样本分组到同一簇中，将不同的样本分组到不同的簇中，从而可以从数据集中找到潜在的相似模式。

目前现有的大多数聚类方法是假设每个样本必须精确地分配给一个类簇，即一个样本只属于一个类簇。然而在实际应用中，一个样本可以同时分配给两个或多个类簇，其在信息不完整或不准确的情况下，很难给出清晰的划分结果。三支决策[5-6]理论认为，人们通常根据现有的信息和证据作决策，然而，如果信息不足或薄弱，则无法做出接受或拒绝的决策，因此，人们可以选择延迟决策来解决这一问题，待获取更多信息后，再给予进一步的决策。于洪[7]将其应用于聚类，并提出了三支聚类的概念，认为一个聚类不再由单一的具有清晰边界的集合表示，而是通过一对集合来表示类簇。随后学者们又对三支聚类的概念进行了进一步的研究。Wang 等[8]采用重叠聚类来获得聚类的支持，再利用扰动分析将核心区域从聚类的支持中分离开来，形成对聚类的三支解释。随后，Wang 等[9]又基于数学形态学的腐蚀和膨胀，提出了三支聚类（CE3）的总体框架。Yu 等[10]提出了一种基于改进的DBSCAN（Density-based spatial clustering of application with noise）的三支聚类，对样本间相似性计算进行了改进，并用一对嵌套集来表示一个类簇。以上聚类算法，虽然考虑了样本间的不确定关系，但主要是针对完备数据集，其对不完备数据集可能并不完全适用。

当聚类算法应用于实际数据集，会出现一个不可避免的问题，就是样本中部分属性值缺失，然而传统的聚类算法不能直接用于不完备的数据集，其只能应用于完备的数据集。为了解决不完备数据聚类问题，国内外学者基于模糊C 均值算法（Fuzzy C-means, FCM）算法提出了一系列改进方法。Aydilek等[11]提出了一种支持向量机和遗传算法的混合方法来估计FCM 算法中的缺失值并对参数进行优化；Li等[12]为区间数据定义了新的距离函数，并扩展经典FCM 以处理缺失数据；Zhang 等[13]利用预先分类的聚类结果设计了一种改进的区间构造方法，并通过粒子群优化寻找最优聚类。

目前，对于不完备数据聚类的研究，大多数方法采取了对缺失值进行填充，然而，缺失值本身就具有不确定性，删除或者填充都会造成一定的误差，进而影响聚类效果。为了有效解决不完备数据聚类问题以及更好地表示样本与类簇的关系，本文提出了一种面向不完备信息系统的集对k-means（Set pair k-means, SPKM）聚类算法。SPKM 算法的主要贡献体现在以下几方面：（1）对于缺失值的处理给出了相应方法，运用集对信息粒的粒化表达方法，将缺失值对应的粒度记为差异度，使得原本聚类过程中不同样本之间距离扩展成包含正同度、差异度和负反度3 个维度的距离定义，可全面地反映聚类效果的正同度、差异度和负反度，比从单一角度衡量更具有系统性。由此根据提出的集对距离度量，获得距离各个样本最近的聚类中心，进而得到初步聚类结果；（2）针对一个样本可能不止和一个类有关系的情况，也给出了相应的聚类方法。对于同时属于多个类的样本，将其分配到相应类的边界域；对于只属于一个类的样本，根据建立的集对联系度公式，将其划分到相应类的正同域或边界域，进而形成由正同域，边界域和负反域表示的集对聚类结果；（3）通过6 个UCI 数据集与其他4 种有代表性的算法进行了实验对比分析，结果表明，该算法可以有效处理具有缺失值的不完备数据集，并且得到较好的聚类效果。

1 基本理论

1.1 不完备信息系统

信息系统又称为知识表达系统，是一个四元组S=(U,A,V,f)，其中U={x1,x2,…,xi,…,xn}是非空有限样本集，称为论域，n为论域中数据样本的个数；A={a1,a2,…,am}是非空有限属性集，m为属性值的个数；V={V1,V2,…,Vm}是U关于A的属性的值域集合，Vs是属性as(1≤s≤m)的值域；f是信息函数，f：vis=f(xi,as)∈Vs，表示样本xi在属性as上的取值为vis。

xi是论域中的第i个样本，其具有A=|m|个属性值，当存在缺失属性值时，信息系统S是不完备的，本文的研究对象是具有缺失值的不完备信息系统。

1.2 集对分析

集对分析是以同、异、反来描述事物的一种理论，通过建立两个事物之间的集对联系度以期来描述确定-不确定性，集对联系度表达式为

式中：S代表属性值相同的数目，P代表属性值相反的数目，F代表属性值既不相同又不对立的数目，N表示属性值的总个数。

式中：a表示正同度，b表示差异度，c表示负反度。其中i∈[-1,1]和j=-1 分别称为差异度和负反度标记符号。

定义1[14]（确定粒集、不确定粒集、确定度和不确定度）设W=(U,A,V)，W0=(U0,A0,V0)，A0⊆A，V0⊆V，R⊆A0，定义W上一对子集，确定粒集和不确定粒集（差异粒集），则对于信息x∈W0，存在一对映射

式中：aR+bR和cR分别称为x关于XC，XU的确定度和不确定度为确定信息粒；为不确定信息粒（差异信息粒）。

定义2[14]（正同粒集、负反粒集、正同度和负反度）基于确定信息粒XC，R⊆A0，定义XC上一对子集，正同信息粒集和负反信息粒集则对于信息x∈XC，存在一对映射

式 中 ：aR和cR分 别 称 为x关 于XCs，XCo的 正 同 度 和 负 反 度为 正 同 信 息 粒 ；为负反信息粒。

图1 数据集示意图Fig.1 Schematic diagram of dataset

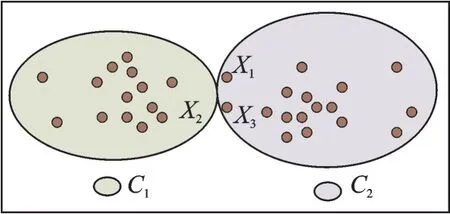
图2 传统聚类结果示意图Fig.2 Schematic diagram of traditional clustering results

1.3 传统聚类结果表示

针对图1 给出的数据集，由传统聚类算法得到的结果如图2所示。图2 中每个样本点被明确地划分到一个类簇，实际上位于中间部分的样本点x1,x2,x3存在不确定信息，不论是将其划分到哪一类，都不能很好地体现聚类结构，导致得到的聚类结果存在误差。

2 基于集对的k-means 的聚类算法

2.1 集对距离度量

衡量样本点之间的距离是聚类过程中非常关键的一步，然而由于缺失值的存在，一些传统的距离计算方法不能直接用于计算不完备数据之间的距离。为此，本文基于集对分析的相关理论，提出了集对距离度量方法，将原本聚类过程中不同样本之间的距离扩展成包含正同度、差异度和负反度3 个维度的距离定义，能有效地处理含有缺失值的不完备数据集。

定义3（集对联系度）假定样本集为U={x1,x2,…,xn}，任意两个样本xp,xq∈U，每个样本xp={vp1,vp2,…,vpm}由m个属性描述，设定阈值为ε1,ε2(ε2＞ε1)，通过标准化后的数据，将样本xp和样本xq建立集对联系度，令满足|vps-vqs| ≤ε1(1≤s≤m)的记为正同信息粒S；满足|vps-vqs|≥ε2的记为负反信息粒P；由于缺失属性值本身就具有不确定性，删除或者填充都会造成一定的误差，然而差异信息粒可以表示模糊、不确定的信息，故将满足ε1＜|vps-vqs| ＜ε2以及缺失的属性值均记为差异信息粒F，则样本xp和xq之间建立的集对联系度为

式中：N代表属性值的总数目；S代表属性值数据差的绝对值小于等于ε1的数目；P代表属性值数据差的绝对值大于等于ε2的数目；F代表其他属性值数目，其包括缺失的属性值。

式（7）也可以简化为

定义4（集对联系度矩阵）设待聚类样本集为U，A为属性集，在关系R下，任取U中的样本xp和xq(p≠q;p,q=1,2,…,n)，令xp与xq建立集对联系度，从而获得集对联系度矩阵T为

式中：apq，bpq和cpq(1≤p≤n,1≤q≤n)满足apq+bpq+cpq=1，其中apq为正同度，bpq为差异度，cpq为负反度。

定义5（集对距离度量）任意两个样本xp,xq(1≤p,q≤n)之间的集对联系度ρpq=a+bi+cj可以通过式（8）得到。根据集对联系度定义了一种集对距离度量方法，可通过正同度a和负反度c的大小来确定与每个样本xp距离最近的样本，即

对任意样本xp，根据式（10）得到与之建立的集对联系度中正同度最大的样本，如果满足条件的只有一个样本，则将其确定为距离样本xp最近的样本，如果满足条件的不止一个样本，则根据条件更为严格的式（11），选取与之建立的集对联系度同时满足正同度最大、负反度最小的样本，将其确定为距离样本xp最近的样本。需要注意的是，对于每个样本xp，找到距离其最近的样本，可能为一个，也可能为多个。

2.2 集对k-means 聚类结果表示

本文将集对信息粒的相关理论引入k-means 聚类中，基于集对信息粒中的正同粒集，差异粒集和负反粒集的定义，提出用正同域Cs，边界域Cu和负反域Co三个域来表示聚类结果。其中，正同域表示属于这个类，边界域表示可能属于这个类，负反域表示不属于这个类。聚类结果如图3 所示，设定了一个边界线用于更好地显示正同域和边界域。

聚类的目的是将相似程度高的样本划分到正同域，使其位于类的中心，将相似程度较低的样本划分到边界域，用这两个域可以更好地表示一个类。这3 个域满足如下性质

（1）Cs(Ci)≠∅

（2）(Cs(Ci)∪Cu(Ci))=U

（3）Cs(Ci)∩Cs(Cj)=∅,i≠j

式中：Cs(Ci)表示类簇Ci的正同域，Cu(Ci)表示类簇Ci的边界域。性质（1）说明，每个类的正同域不能为空；性质（2）说明U中的任何一个样本必须属于一个正同域或者至少属于一个边界域；性质（3）说明任何一个样本最多只能属于一个类的正同域。

图3 聚类的可视化Fig.3 Visualization of clustering

2.3 算法描述与分析

集对k-means 聚类算法可以用于处理存在缺失值的不完备数据集。缺失值处理的主要思想是将样本的缺失属性值在进行集对分析时，将其粒度记为相应的差异度。另外，其是用正同域、边界域共同来表示一个聚类，而不是一个单一的集合。然而传统k-means 聚类算法是用具有清晰边界的集合来表示一个聚类，其思想是先初始化k个聚类中心，作为k个初始类簇，然后将每个样本依次分配到各个类簇。但在聚类过程中只考虑了两种关系，会降低对不确定点划分的准确性，而样本与类簇之间存在属于、可能属于、不属于这3 种关系。针对这3 种关系的划分，本文实验中的聚类任务分为两阶段，第1 阶段构造包含正同域和边界域的集合，第2 阶段使正同域和边界域分离。

第 1 阶段：假定样本集为U={x1,x2,…,xn}，选取的k个初始聚类中心为{μ1,μ2,…,μk}。将样本集数据先进行标准化处理，再通过式（8）依次将样本xp(1≤p≤n)与各聚类中心μj(1≤j≤k)建立集对联系度。根据集对距离式（10)和(11）得到距离每个样本最近的聚类中心，将样本xp分配到与之距离最近的类簇Cλq=Cλq∪{xp}，由此确定每个样本的簇标记λq。在迭代过程中，新聚类中心的计算公式为

式中：x∈Cj，x={v⋅1,v⋅2,…,v⋅m}，j=1,2,…,k，|Cj|表示类簇Cj的元素个数。

上述过程得到了聚类的初步结果，将类中样本分为两种类型，即

第2 阶段：对初步聚类结果进行细分，使得正同域和边界域进行分离。第1 种类型的样本{xi∈Ci|∃j=1,2,…,k,j≠i,xi∈Cj}，显然，其与多个类簇存在关系，则将其同时分配到类簇Ci的边界域Cu(Ci)和类簇Cj的边界域Cu(Cj)。对于第 2 种类型的样本其只属于一个类簇Ci中，不再属于其他任何类簇Cj(j≠i)，只需判断其位于正同域还是边界域。计算方法如下：设定正同度阈值为α，负反度阈值为β，计算该样本与所在类的聚类中心的集对联系度，比较其正同度、负反度与阈值之间的大小关系，将类中样本依次分配到相应类簇的正同域Cs或边界域Cu，公式为

基于以上讨论，集对k-means 聚类的结果可表示为

式中：Cj={Cs(Cj)∪Cu(Cj)}(1≤j≤k)表示一个类簇的聚类结果。对于图1 中的样本点，本文所提SPKM 算法得到的聚类结果如图4 所示。

图4 集对k-means 聚类示意图Fig.4 Schematic diagram of set pair k-means clustering

2.4 算法流程

算法步骤如下：

输入：样本集U={x1,x2,…,xn}，类簇数目k，参数ε1,ε2,α,β

输出：聚类结果C={{Cs(C1)∪Cu(C1)},{Cs(C2)∪Cu(C2)},…,{Cs(Ck)∪Cu(Ck)}}

（1）随机选取k个样本作为初始聚类中心{μ1,μ2,…,μk}

（2）Repeat

（3）令Cj=∅ (j=1,2,…,k)

（4）Forp=1,2,…,ndo

（5） 对于每个样本xp(1≤p≤n)，根据式（10）和（11）计算得到与之距离最近的聚类中心μj

（6） 令λj为簇标记如果满足 max {apj}的样本不唯一，则增加条件min {cpj}，选择

（7） 将样本xp分配到类簇Cλj=Cλj∪{xp}中

（9）End for

（10）直到|μ′j-μj| ＜δ或者达到最大迭代次数

（11）Forj=1,2,…,kdo

（12） 对于类簇Cj中的每个样本x，依次计算H={x：x∈Cj,∃i,i≠j,x∈Ci}；

（13） IfH≠∅ then

（14） 将样本x同时分配到类簇Ci和类簇Cj的边界域Cu

（15） Else

（16） 根据公式Cs={a≥αorc＜β}，Cu={0 ＜a＜αandc≥β}，将样本分配到类簇Cj的正同域Cs(Cj)或者边界域Cu(Cj)

（17） End if

（18）End for

（19）输出C={{Cs(C1)∪Cu(C1)},{Cs(C2)∪Cu(C2)},…,{Cs(Ck)∪Cu(Ck)}}

上述算法主要分为两个阶段：第1 阶段（步骤(1)～(10)）是构造包含正同域和边界域的集合。在步骤(5)～(7)中，是对存在缺失值的样本，根据本文提出的集对距离度量方法，计算得到距离每个样本最近的聚类中心，由此将每个样本分配到距离最近的类簇中。为了减少初始聚类中心对聚类结果的影响，在每次分配一个样本后，根据步骤（8）对聚类中心进行更新，进而将所有样本分配到k个类簇中，得到初步聚类结果。第2 阶段（步骤（11）～（18）)是将正同域和边界域分离，在步骤(12)中判断每个样本是否只存在一个类中，将样本分为只属于一个类和属于多个类两种情况，分别对其采取不同划分方法。步骤（13）～（14）处理的是属于多个类的样本，将其同时分配到这些类簇的边界域，步骤(16)处理的是只属于一个类的样本，根据式（13）进行计算，进而将其分配到类簇的正同域或者边界域，由此得到两个域共同表示的集对k-means 聚类结果。算法流程图如图5 所示。

2.5 算法复杂度分析

针对时间复杂度，设论域中的样本数目为n，聚类数目为k，属性数目为m。SPKM 算法的时间复杂度主要由预处理过程中的数据标准化、步骤（5）中依次对每个样本计算距离和步骤（12）～（16）中将样本划分到相应类簇的正同域或边界域产生。数据标准化过程中，需要对每个样本都进行处理，每个样本有m个属性，故产生的时间复杂度为O(mn)；每次迭代计算各个样本与聚类中心的距离产生的时间复杂度为knm，设迭代次数为I，则这部分的时间复杂度为O(knmI)；对于每个样本划分到相应类簇的正同域或边界域，须对类中每个元素xp(p=1,2,…,n)与所在类簇Cj(j=1,2,…,k)的聚类中心依次进行计算，这部分产生的时间复杂度为O(knm)。所以，SPKM 算法的时间复杂度为O(n)=O(mn)+O(knmI)+O(knm)。本文算法在没有增加时间复杂度的前提下，解决了存在缺失值的数据空白问题，提高了聚类效果。

图5 集对k-means 聚类算法流程图Fig.5 Flow chart of set pair k-means clustering algorithm

针对空间复杂度，SPKM 算法处理的样本数目是n，初始聚类中心的数目是k个，样本的属性值的维数是m，故SPKM 算法的空间复杂度为O((k+n)m)。

3 模型验证

为了评估所提出的SPKM 算法的性能，进行了一系列实验，主要分为两方面：一是对算法参数进行分析，二是选取了4 种具有代表性的算法进行对比分析。本文所提算法和对比算法是在一台DELL（Windows 10，Intel（R）Core（TM）i5-8300H，CPU@ 2.30 GHz 2.30 GHz）计算机上使用Python3.7 环境实现的。

3.1 数据集选取与评价

聚类的评价，又被称为聚类有效性，是评估学习方法在聚类方面表现的关键过程，度量方法将影响到几种聚类方法的性能比较。为了验证本文算法的性能，选取了UCI 中的6 个数据集Iris，Wine，Seeds，Liver disorders，Wave form 以及Page blocks，表1 给出了这些数据集的大小、属性个数和类簇个数。

对于数据集：U={x1,x2,…,xn}，假定通过聚类得到的聚类结果为C={C1,C2,…,Ck}，数据集的真实聚类结果为令λ和λ∗分别表示C和C∗对应的簇标记，将样本两两配对考虑，定义

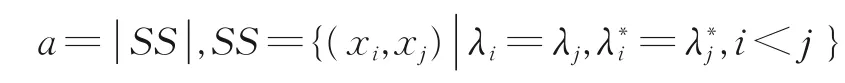
表1 实验数据集的描述Table 1 Description of lab datasets

本文选取几种常见的聚类性能度量指标。

（1）MacroF（1宏平均）

作为一个多标签任务的衡量指标，MacroF1可表达为

式中

式中：TPCi表示Ci中样本被正确聚为该类的数量；FPCi表示非Ci中样本被错误聚为该类的数量；FNCi表示Ci中样本被错误聚为其他类的数量。MacroF1性能度量的结果在区间[0,1]。

（2）Accuracy（准确率）

式中：φk为簇Ck中正确划分的样本数目，n为样本的总数。准确率越高，聚类结果越好。

（3）JC（Jaccard 系数）

（4）FMI（FM 指数）

（5）ARI（兰德指数）

式中：|Ci|为类簇Ci的样本数目；||为真实类簇的样本数目表示类簇Ci和真实类簇共同拥有的样本数目。

3.2 SPKM 算法参数分析

以Iris 数据集为例，对算法在不同参数下的性能进行了详细分析。由于数据集是经典完备数据集，需要对其进行处理，随机生成带有缺失值的不完备数据集，本文选取的缺失率为5%，10%，15%和20%，通过使用评价指标JC，FMI 和ARI 对该聚类算法的性能进行评价。图6 给出了3 个评价指标平均值随着4 个参数变化的波动情况。表2 给出了Iris 数据集在最优参数下的聚类结果。由于本文提出SP-KM 算法是以正同域和边界域来表示聚类结果，所以在每个指标下都分别给出了单独的正同域Cs以及正同域和边界域Cs∪Cu这两个评价结果。

图6 数据集Iris 的参数变化结果Fig.6 Result of parameter changes in Iris dataset

首先讨论的是参数ε1，ε2，以运行100 次的均值作为一次实验值，进行大量实验，图6（a2）是相对图6（a1）的一个局部图，是通过缩小步长进行的更为精细的处理，得到最佳参数为ε1=0.16,ε2=0.79，其对应的100 次均值的最大实验值达到0.87（正同和边界域），最优值在图中已用红色三角进行区分。然后保持ε1=0.16,ε2=0.79 不变，讨论参数α和β。用同样的方法得到的最佳参数为α=0.6,β=0.09，其对应的100 次均值的最大实验值达到0.922（正同域），0.923（正同和边界域）。从图6 可知数据集Iris 的最优参数为ε1=0.16,ε2=0.79,α=0.6,β=0.09。对于其他5 个数据集也通过实验方式得出了最优参数，具体结果如表3 所示。

表2 Iris 数据集在最优参数下的性能分析Table 2 Performance analysis of Iris dataset under optimal parameters

表2 给出的是数据集Iris 在最优参数下的聚类结果，可以看出在指标JC，FMI 和ARI 下均得到了较好的聚类效果。其中，针对正同域和边界域Cs∪Cu，在缺失率为5%的情况下得到的JC 指数为0.993，FMI 为 0.987，ARI 为 0.980；在缺失率为 10% 的情况下达到了 JC 为 0.973，FMI 为 0.947，ARI 为0.921。同时，从表中也可以看到，针对正同域Cs，得到的评价指标的值均低于在Cs∪Cu下的。这是因为这两个集合是通过对二支聚类的收缩或扩展得到的，所以Cs∪Cu的性能优于Cs是合理的。通过这3个指标的实验结果可以分析出，随着缺失率的增加，聚类质量下降，究其原因是缺失率越大，不确定信息越多，其对样本划分产生的影响越大。

在最优参数下，对Iris 数据集的集对k-means 聚类结果进行了可视化，结果如图7 所示。从图7 可知，数据集被聚成了3个类簇，每个类簇通过正同域和边界域两个域共同表示。从图7 可以看出，同时属于多个类簇的样本位于多个类簇的交界处，将其分配到边界域是合理的；对于只属于一个类，但其位于类簇的边缘区域的样本，将其分配到边界域也是合理的。

3.3 SPKM 算法的实验对比分析

为了识别SPKM 算法的聚类质量，通过评价指标Accuracy，MacroF1，JC，FMI 和 ARI 与选取的 4 种算法进行了对比分析。第1 种是Wang 等基于数学形态学的腐蚀和膨胀提出的三支聚类框架（CE3-k-means）[9]；第 2 种是 Yu 等基于改进的 DBSCAN 提出的三支聚类算法（3W-DBSCAN）[10]；第3 种是Zhang 基于三支权重和三支分配，提出的一种三支c-means 聚类算法[15]，依照原文将其记为TCM；第4 种是Yang 等基于密度峰值提出的不完备三支聚类算法，依照原文将其记为Adopted methods[16]。

表3 6 个数据集的最优参数Table 3 Optimal parameters for six datasets

图7 Iris 数据集最优参数下聚类结果Fig.7 Clustering result under optimal parameters of Iris dataset

将对所有正同域和边界域形成的聚类结果进行实验评价。由于本文的研究对象是不完备数据集，故将选取的6 个数据集按照5%，10%，15%，20%的比例作随机缺失处理。本文所提算法和4 种对比算法在5 个评价指标下的聚类结果如表4—8 所示。在不同算法之间的最优结果用粗体进行标记。

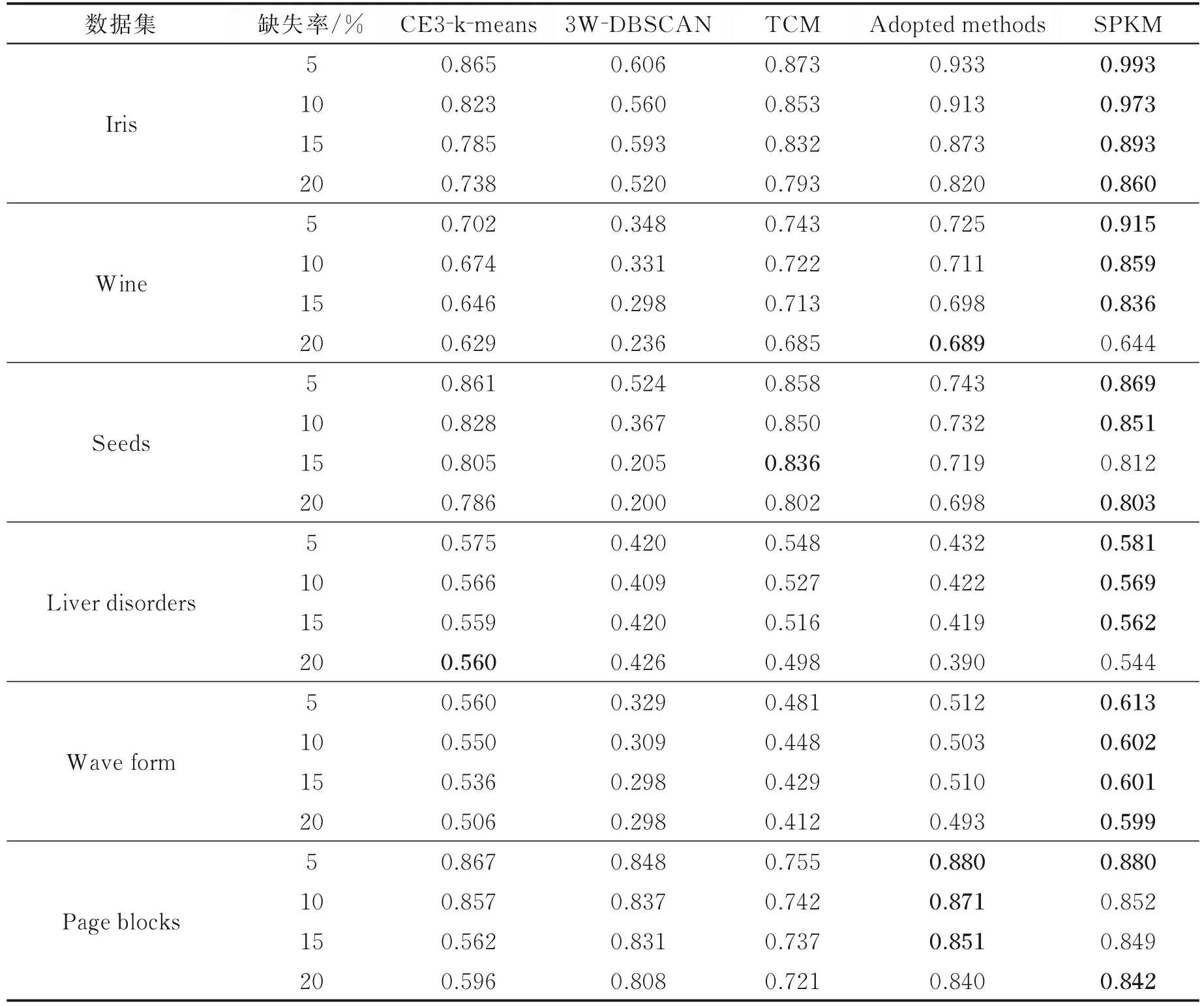
表4 5 种算法在指标Accuracy 下的对比结果Table 4 Comparison results of five algorithms under index Accuracy

表5 5 种算法在指标Macro F1下的对比结果Table 5 Comparison results of five algorithms under index Macro F1

续表

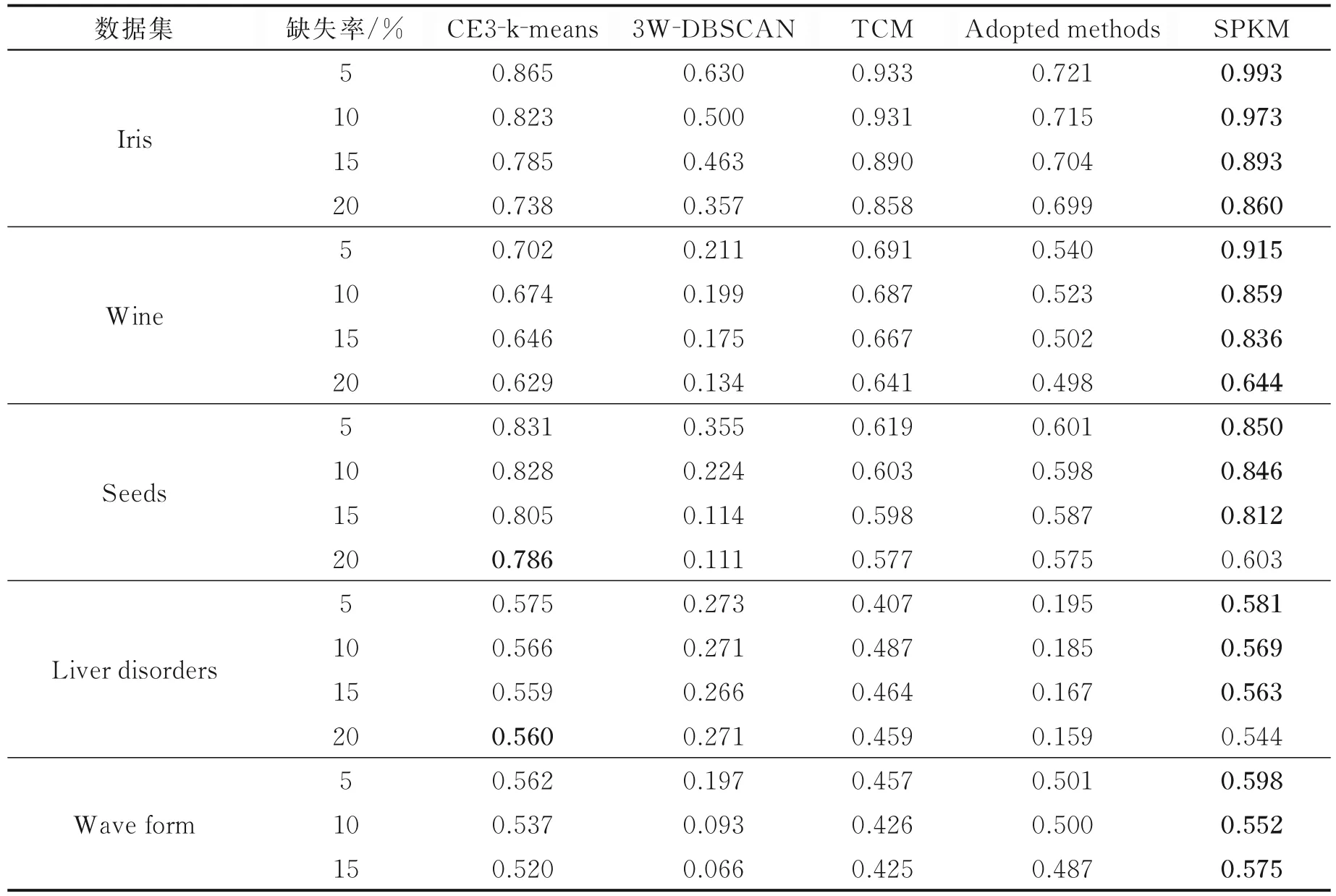
表6 5 种算法在指标JC 下的对比结果Table 6 Comparison results of five algorithms under index JC

续表

表7 5 种算法在指标FMI 下的对比结果Table 7 Comparison results of five algorithms under index FMI

表8 5 种算法在指标ARI 下的对比结果Table 8 Comparison results of five algorithms under index ARI

续表

从表4 中的实验结果可知，SPKM 算法在评价指标Accuracy 上得到的聚类结果要优于对比算法，特别是在数据集Iris，Liver disorders 和Wave form，该算法的准确率均高于对比算法。对于数据集Wine 和Seeds，本文算法在4 个缺失率下，都能达到在3 个缺失率下优于对比算法，其中Wine 在缺失率为20%时，比最优算法低了0.045，Seeds 在缺失率为15%时，能做到优于3 个对比算法。针对数据集Page blocks，在缺失率为5%和20%时，准确率仍高于所有对比算法，但在缺失率为10%，15%时，与最优对比算法Adopted methods 相比分别下降了0.019，0.002，但仍比其他3 个对比算法的效果要优。

从表5 的实验结果可以看出，对于数据集Iris，Wine，Liver disorders 和Wave form，用评价指标MacroF1得到的聚类结果要明显高于对比算法，也体现出了SPKM 算法的优越性。对于其他两个数据集也得到了不错的聚类结果，比如数据集Seeds，在缺失率为15%的情况下，即使它不是最好的算法，但在缺失率为5%，10%和20%时，MacroF1值要高于其他4 个对比算法。从表6 中的实验结果可以看出，对于数据集Iris，Wine 和Wave form，用评价指标JC 得到的聚类结果均优于对比算法。从表7 中的实验结果可知，在4 个缺失率下数据集Liver disorders 和Wave form 得到的聚类结果均优于对比算法。从表8 的实验结果可知，对于数据集Iris 和Wine，用评价指标ARI 得到的聚类结果要明显高于对比算法。综上所述，本文提出的聚类算法可以有效处理含有缺失值的不完备数据集，而且具有良好的聚类性能。

4 结束语

针对不完备数据的聚类问题以及为了更好地表示样本与类簇的关系，本文将集对分析的相关理论引入到k-means 聚类中，提出了一种面向不完备信息系统的集对k-means 聚类算法，将聚类结果划分为3 部分，用正同域Cs，边界域Cu，负反域Co表示。本文提出的集对k-means 聚类算法，将原本聚类过程中不同样本之间距离扩展成包含正同度、差异度和负反度3 个维度的距离定义，有效解决了不完备数据集的距离度量问题，并基于这个定义扩展了k-means 聚类算法，很好地表示了样本与类之间的3 种关系。同时，对于样本可能和多个类有关系的情况，也给出了相应的聚类方法，将其划分到相应类的边界域。实现了对聚类结果结构的改进以及聚类准确率的提高。通过对6 个UCI 数据集进行对比实验，结果表明该算法可以有效解决具有缺失值的不完备数据集，并且改善了聚类结构。然而，参数的变化对聚类结果的影响较大，如何获取更为合适的参数也是下一步的工作，其将对提高聚类质量有重要影响。