考虑建筑物刚度和自重的地层位移解析解

王 鑫，胡继伟，杜 洋，杨柳君，熊咸玉

(1.西安科技大学建筑与土木工程学院，陕西 西安 710054；2.中色科技股份有限公司，河南 洛阳 471039)

0 引 言

为保证地铁隧道在城市建筑密集区施工的安全，众多研究学者对地层沉降预测进行了研究。Boscardin等[1]研究表明，在城市人口和建筑物密集区域地铁开挖过程中会引起地表横向和纵向运动。Melis、Vorster等[2-3]发现，地铁开挖地面沉降不仅对地下的结构物造成危害，对地面上的建筑物也会产生影响。经验方法中，Verruijt等[4]对Sagaseta 的镜像法进行了修正；Kasper[5]通过有限元法对盾构隧道的沉降特性进行了研究；Frischmann等[6]分析地铁隧道施工下穿砌体框架结构的地面沉降情况得出，研究隧道施工对建筑物影响时需考虑建筑物自身刚度问题；Chaberi[7]利用数值方法研究了隧道深度和地面荷载影响下的地表沉降；Tang等[8-9]采用最大似然估计方法拟合Peck公式，采用纵向表面垂直和水平位移的耦合计算公式，得出既有建筑物会增加地铁施工引起的地表纵向和横向位移的结论；Dimmock等[10]考虑建筑物刚度，提出一种简化预测地铁施工引起的土体变形的方法；欧阳文彪等[11]结合了等效刚度原理，给出隧道下穿既有建筑的地层沉降位移；王剑晨等[12]采用等效替换，建立了新旧隧道和围岩三者作用的模型；张在明等[13]考虑修正刚度法，针对多层砖混结构，研究在隧道施工过程中可能造成的建筑损坏。随着人工智能的进步，许多研究学者将人工神经网络应用于开挖隧道引起的地表沉降预测模型中[14-15]。在地铁施工中，建筑物自身刚度和自重都会影响地层位移，刚度能约束地层位移，自重会增大地层位移。因此，上述研究仅考虑建筑物刚度对地层位移的影响与实际情况不符。

本文以西安地铁工程为依托，基于当层法得出建筑物刚度对地层竖向位移计算公式；将建筑物自重等效为均布荷载，通过太沙基理论分析建筑物自重对地层竖向位移的影响，得出地层竖向位移计算公式；结合平面应变原理，推导出考虑建筑物刚度和自重时地层水平位移计算公式，计算结果与实际模拟数据较为吻合，对实际工程有一定的参考价值。

1 地层位移简化模型

在隧道施工时，地层会因为土层减少和应力释放发生变形。一方面，上部建筑物由于刚度作用会约束地层的变形；另一方面，建筑物自重产生的基底附加压力对土体产生不等量的横向挤出和竖向压缩。因此，计算地铁施工产生的地层位移需同时考虑既有建筑物的自重和刚度。引入当层法解决地层刚度不匹配问题。当层法[16]基本思想为将不同厚度的材料通过刚度进行等效，将多层材料变为均匀质体。当层法地层等效代换示意见图1。图1中，A为地表土层；B为建筑基础下方土层；d为A、B之间土层厚度；H′为地表到隧道中心距离；A′、B′分别为A、B通过当层法进行等效代换土层；d′为A、B之间土体和基础转化厚度。通过相对刚度法计算考虑建筑物刚度时地层沉降值，再通过将上部建筑物荷载转化为均布荷载，结合太沙基理论计算考虑建筑物自重时地层沉降值。

图1 当层法地层等效代换

2 地层竖向与水平位移计算

2.1 当层法地层厚度转化

为模拟地铁施工对建筑物的影响，需计算建筑物底部的位移。通过解析解计算建筑物底部位移时，需考虑建筑物与土体相对刚度的影响。地铁施工会使隧道周围土体应力释放，引起地层纵向沉降和水平位移，进而使建筑物底部产生位移。假设建筑物底部和土体接触边界为整体接触，地铁施工不会造成接触部位分离，将建筑物和土体视为接触良好的2种不同材料。当层厚度d′计算公式为

d′=d(E1/E2)0.5

(1)

式中，E1为A、B之间土体和基础的弹性模量；E2为B层以下土体的弹性模量。通过当层法能将建筑物刚度的影响转化为实际的地铁隧道埋深增加对地层沉降的影响，通过peck经验公式对地层沉降进行计算。

2.2 基于Peck经验公式的土层竖向位移

Peck公式常用来计算因隧道施工造成的地表沉降，其相应的地层沉降量估算公式为

S(x)=Smaxexp(-x2/2i2)

(2)

式中，S(x)为沉降量；Smax为隧道中心线处最大沉降量；i为沉降槽宽度；x为距隧道中心线的距离。

地层沉降槽宽度i和地铁隧道埋深H′之间为线性关系，即

i=KH′

(3)

式中，K为地层沉降槽宽度系数。

对式(2)两边积分得

(4)

式中，R为隧道开挖盾构半径；Vl为上部不存在建筑物时的地层损失率。

Mair[17]认为，任意深度土体沉降同样符合Peck公式。任意深度土体沉降槽宽度iz的计算公式为

iz=Kz(H-d)

(5)

式中，z为地层深度；Kz为地层深度为z处的沉降槽宽度系数，当z=0时，式(5)、(3)相同。

韩煊[18]认为，Kz可以通过下式计算

(6)

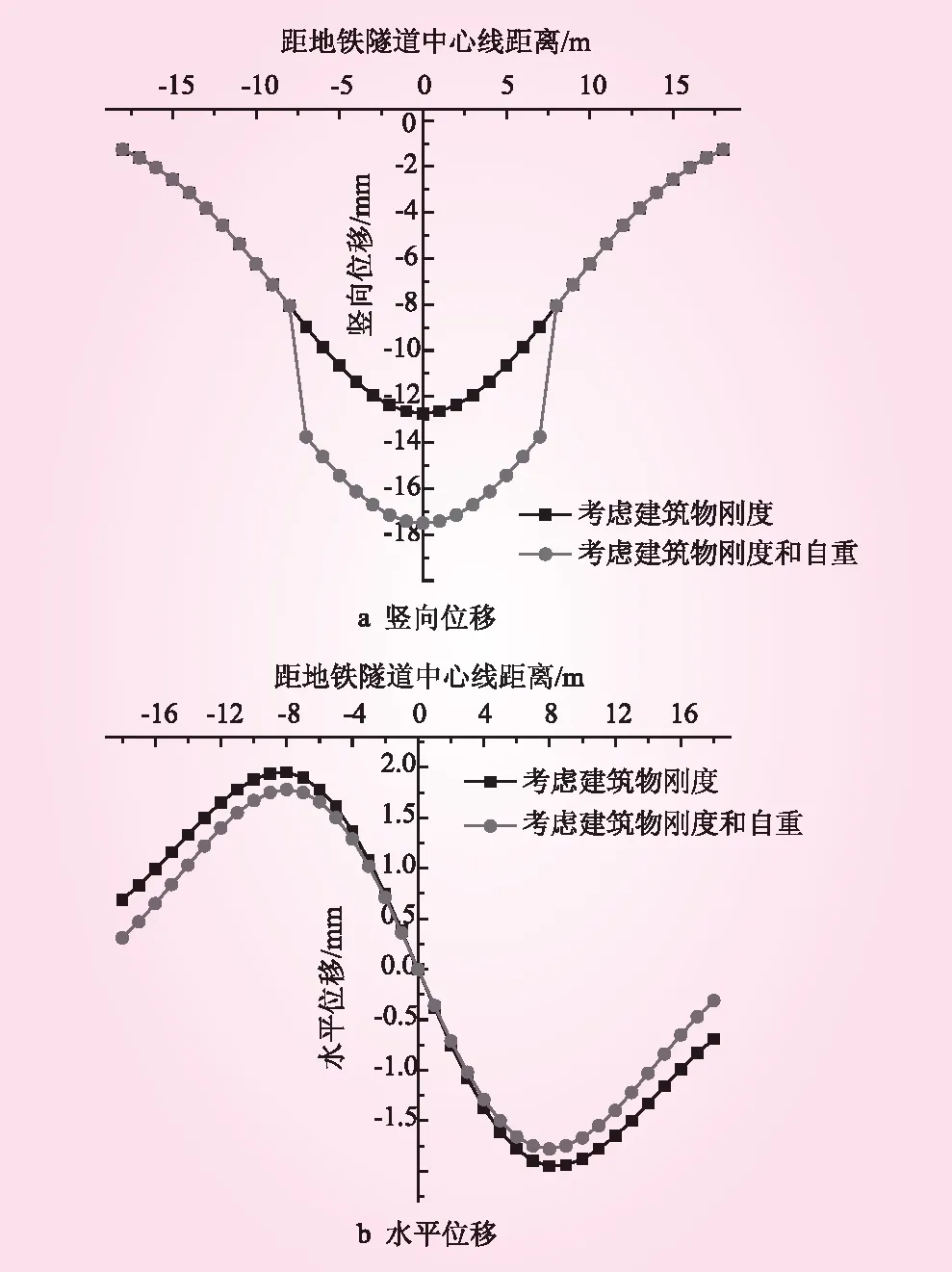
式中，系数a取值为0

将式(6)代入式(5)可以得出地层d深度处的沉降槽宽度iz为

iz=K(H-az)

(7)

将式(3)、(7)代入式(2)可得土体在z深度处的竖向位移为

(8)

2.3 沉降槽宽度系数K和地层损失率Vl

沉降槽宽度系数K计算公式如下

(9)

式中，φ为土体内摩擦角。

Lee等[19]用等效土体损失参数g来计算土层土体损失量，地层损失率Vl计算公式为

(10)

(11)

式中，g为等效间隙参数；系数α取0.2～0.3，Gp为盾构机与衬砌之间的几何空隙；U3D为盾构机前部土体的三维弹塑性变形；Δ为盾尾厚度；δ为衬砌拼装空间；Ui为土层三维弹塑性变形；νu为不排水泊松比；Cu为不排水抗剪强度；Eu为不排水弹性模量；N为稳定系数。

表1 各层土的物理力学性质

2.4 考虑建筑物自重的地层竖向位移和水平位移

将建筑物底部与地层接触面等效为1个长方形面积，考虑到地层为不排水固结，采用太沙基一维固结理论，建筑物自重对地层产生的位移计算公式为

S(z)=(P+γz)(H-z)/E

(12)

式中，p为建筑物对地层产生的均布压力；γ为深度为z处土的容重；(H-z)为土层z处到地铁隧道顶端土层厚度；E为土层加权弹性模量，可按下式计算

(13)

式中，d1，d2，…，dn分别为1～n地层厚度。

地层A′竖向位移计算公式为

S(x，z)=S′(x，z)+S(z)

(14)

式中，S(x，z)为地层z深度处的竖向位移。

根据平面应变原理，剪应变分量为0，即

(15)

(16)

式中，U(x，z)为地层z深度处的土体水平位移；c为常数。

结合式(15)、(16)得到土层水平位移U(x，z)计算公式

(17)

当x=0时，U(x=0，z)=0，代入式(17)得c=0。此时，地层的水平位移公式为

(18)

3 实例验证与分析

为验证考虑建筑刚度和自重情况下地层位移的可行性，得出更优的描述地表沉降曲线理论，引用王涛[20]的工程案例并与之比较，分析地铁隧道在建筑物正下方穿越时地表竖向位移。

3.1 实例验证

文献中砌体结构的尺寸为：高8 m、长20 m、宽10 m；隧道开挖半径为3 m，埋深为9 m。各层土的物理力学性质见表1。将考虑建筑物刚度和自重、仅考虑建筑物刚度计算出的地表竖向位移与文献数据比较，结果见图2。从图2可知，采用只考虑建筑物刚度计算出的地表沉降曲线和文献中地表沉降曲线的形态差异较大，前者为高斯曲线，而考虑建筑物刚度和自重的地表沉降曲线为塞形曲线，与文献中沉降曲线更相近。

图2 地表沉降比较

为了评价2种预测效果，对预测数据和文献数据进行方差比较结果表明，考虑建筑物刚度和自重计算的地表竖向位移值和文献竖向位移值的总方差较小，计算结果更符合。

3.2 实例分析

3.2.1计算参数

根据勘察资料，西安地铁开挖的隧道穿越建筑物各层土的物理力学性质见表2。

表2 各层土的物理力学参数

U3D=0，隧道埋深H′=18.3 m，开挖半径R为3.08 m，理论间隙参数Gp=0.155 m，稳定系数N为1.715，将表1中各参数的加权平均值代入式(3)后可得Ui=0.024 2，α取0.2，g=0.039 1 m，地层损失率Vl=1.27%，将表1中各参数的加权平均值代入式 (1)后可得沉降槽宽度系数K=0.55。

建筑物为钢筋混凝土框架结构，地铁在正下方穿过。基础埋深4 m，地面以上建筑高度为24 m。建筑采用C30混凝土，弹性模量为30.0 GPa，泊松比为0.2，密度为2 500 kg/m3，d=4 m，H′=18.6 m，建筑物自重M=1 133.58×109N。

3.2.2地层位移计算

根据式(14)、(18)，结合本工程条件计算出地层竖向位移和水平位移，并与只考虑建筑物刚度的计算结果相比较，结果见图3。从图3可知：

图3 地层位移对比

(1)地层深度z=0时，考虑建筑物刚度时计算出的地层沉降曲线符合一般的高斯曲线规律，考虑建筑物刚度和自重时计算出的地层沉降曲线为塞形。在建筑宽度范围内，同时考虑建筑物刚度和自重计算出的地层竖向位移明显大于不考虑自重的竖向位移，即在建筑宽度附近处竖向位移会产生突变。考虑建筑物刚度和自重时下方地层的最大竖向位移为17.5 mm，只考虑建筑刚度的最大竖向位移为12.7 mm。距离地铁隧道中心线超过7 m的范围后，建筑自重的影响就变得很小。

(2)只考虑建筑物刚度时计算出的地层水平位移曲线与考虑建筑物刚度和自重时计算出的地层水平位移曲线在距离隧道中心线4 m范围内时基本重合，考虑建筑物刚度和自重时只考虑建筑物刚度时计算出的地层水平位移小；随着距地铁隧道中心线距离的增大，2种情况下计算的地层水平位移差值增大，最大差值为0.38 mm。

考虑建筑物刚度和自重时计算出地层竖向和水平位移与地层深度有关，考虑地层深度z=0、5、10、15、20 m时地层的竖向和水平位移见图4。

图4 地层位移

从图4可知：

(1)考虑建筑物刚度和自重时计算出的竖向位移曲线形态存在差异。z=0、5m时，竖向位移曲线呈塞形；z=10、15、20 m时，竖向位移曲线呈一般的高斯曲线，说明随着深度的增加，建筑物宽度范围处竖向位移突然变化的这种趋势越来越平缓。随着地层深度z的增大，竖向位移的最大值增大，z=20 m时的最大竖向位移为32.2 mm，但是曲线反弯点处的竖向位移减小。

(2)考虑建筑物刚度和自重时计算出的地层水平位移曲线形态存在差异。随着地层深度z的增大，水平位移曲线变得相对较陡；随着距离隧道中心线的距离增加，水平位移先快速增加后快速减小随后趋于稳定。随着地层z的增加，最大水平位移增大；z=20 m时的最大水平位移为4.9 mm，水平位移最大值出现的位置相对靠近地铁隧道中心线；z=20 m时，距地铁隧道中心线距离为3 m。

4 结 语

本文以西安地铁工程为依托，考虑既有建筑物的刚度和建筑物自重计算地铁施工引起的地层位移，主要结论如下：

(1)考虑既有建筑物的刚度和建筑物自重情况时，随着深度增加，建筑物宽度范围处竖向位移曲线突然变化的趋势越来越平缓，竖向位移曲线由塞形变为高斯曲线，但最大竖向位移在增大。不同地层深度处的水平位移曲线形态相似，随着深度增加，水平位移曲线斜率变大，水平位移最大值随之增加并且最大水平位移出现的位置逐渐向隧道中心线靠近。

(2)考虑建筑物刚度和自重地表竖向位移方差较小，与实际情况较为相近。在隧道上方的建筑物宽度范围附近，地表土层竖向位移会快速增加且明显大于不考虑自重的情况，竖向位移曲线为塞形。