缓倾顺向软弱夹层岩体边坡变形机理及稳定性研究

陈权川，朱爱军，2，殷 博，涂芳瑞，袁千城

(1.贵州大学土木工程学院，贵州 贵阳 550025；2.贵阳建筑勘察设计有限公司，贵州 贵阳 550009；3.贵州省建筑设计研究院有限责任公司，贵州 贵阳 550081)

0 引 言

缓倾顺向岩坡指岩层倾向与坡面倾向一致或近于一致且岩层倾角在15°左右的层状边坡。此类边坡在降雨、地震等各种不利因素作用下易发生滚石、滑坡、崩塌等地质灾害，尤其是含软弱夹层时，由于软弱夹层的强度远远低于周围岩层，表现为边坡失稳破坏的控制性滑移面[1]。缓倾顺向软弱夹层岩体边坡广泛分布于我国西南地区，诱发的地质灾害相对较多，专家学者对此非常关注。龚文惠等[2]等运用弹塑性理论探讨了结构面强度、岩层厚度、岩层倾角对顺层岩质边坡稳定的敏感性；李安洪等[3]总结并讨论了顺层岩质边坡常见的滑移-拉裂、滑移-弯曲2种破坏模式的稳定性分析方法；韦达[4]运用地质力学理论探讨顺层岩质边坡的破坏机理，并根据深梁理论揭示出岩层变形与纵向开挖长度的相关性；王学伍等[5]采用有限差分软件FLAC3D探讨了地震作用下含软弱夹层的顺倾岩质边坡加速度放大效应和软弱夹层区域加速度放大系数的变化规律；范刚等[6]基于大型振动台模型试验和传递函数理论，探讨了含软弱夹层顺层岩质边坡的绝对传递函数和相对传递函数计算边坡动力特性参数的准确性，并对利用传递函数估算边坡频域动力响应的可行性进行了研究；宋子岭等[7]综合极限平衡法和强度折减法，对开挖70°的含多层软弱夹层边坡进行稳定性研究表明，极限平衡法计算的稳定系数较有限差分强度折减法大；程伟等[8]运用FLAC3D软件分析了岩体边坡应力和变形在分部开挖过程中的发展规律，对边坡的稳定性进行了评价；范昊天等[9]采用离散元软件PFC2D详细分析了含软弱夹层岩质边坡滑动的演化过程和破坏机理。

为较好地分析含缓倾顺向软弱夹层岩体边坡稳定性和破坏机理，本文依托贵州仁怀某岩体边坡，结合勘察资料，采用FLAC3D中的应变软化模型(软弱夹层)和摩尔-库仑模型(软弱夹层周围岩体)对垂直开挖后的岩体边坡变形过程进行研究，并结合极限平衡法讨论了软弱夹层抗剪强度对此类边坡稳定的敏感性，可为该类边坡的稳定性分析和支护治理提供参考。

1 基本原理

1.1 强度折减法

强度折减法的原理指对边坡岩土体的抗剪强度参数(粘聚力c和内摩擦角φ)逐步进行折减，以折减后获得的粘聚力c′与内摩擦值φ′带入求解，不断增加折减系数，反复计算，当边坡从稳定状态到失稳破坏致使塑性区贯通时，认为模型完成收敛，边坡处于临界破坏状态，此时边坡岩土体的实际抗剪强度值与折减完成后的抗剪强度的比值即为边坡的安全系数Fs。公式如下[10]

(1)

1.2 应变软化模型理论

该模型是在摩尔-库仑模型的基础上形成的，屈服函数、势函数、塑性流动规律和应力修正与摩尔-库仑模型一致，且具有非关联剪切和关联拉伸流动规律。不同之处在于，材料进入塑性屈服后，内聚力、内摩擦角、膨胀角和拉伸强度均可发生软化，可定义为非线性阶段函数，而在摩尔-库仑模型中，这些性质被认为是不变的。在弹性阶段应变仅由弹性应变ee组成，即e=ee；在屈服点之后，总应变为弹性应变ee和塑性应变ep两者之和，即e=ee+ep[11]。应变软化模型见图1。

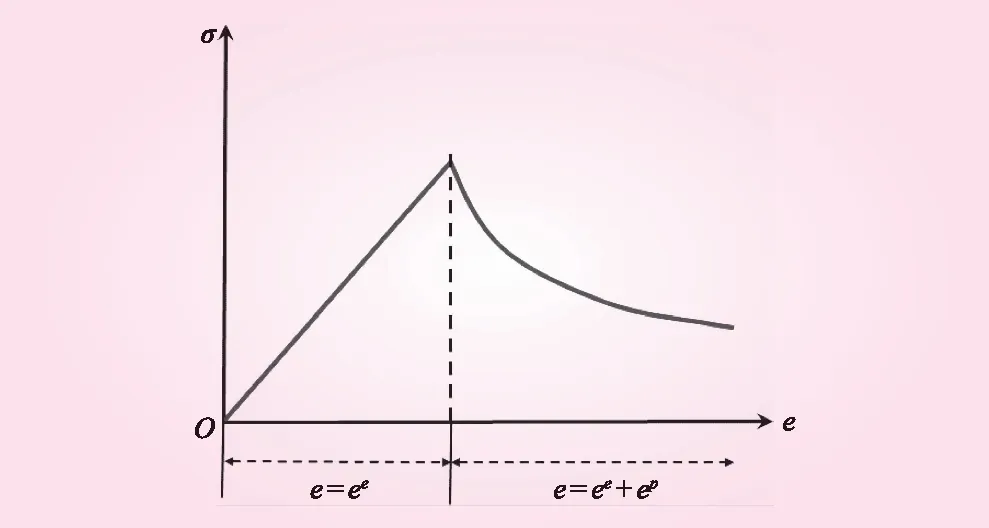
图1 应变软化模型

2 模拟方案

2.1 工程背景

研究边坡的天然地形坡度为10°～23°，局部伴有陡坎发育，场区地层结构简单且地下水位较深，无不良地质现象发育，含有强～中风化石英砂岩和红粘土组成的软弱夹层。其中，强风化岩层较薄且风化程度较高，中风化岩层较破碎且较坚硬，软弱夹层力学性质较差。岩层倾向与边坡坡面近于一致，属于缓倾型顺向坡。

2.2 模型建立

以工程典型剖面为原型建立FLAC3D模型。为获得较为准确的计算精度，边坡的模型以实际工程为背景，结合学术界广泛认可的模型尺寸加以确定[10]。由于拟建边坡所含软弱夹层较多，为便于研究，减少计算量，提高效率，建模时仅选取1条软弱夹层重点研究。边坡模型尺寸见图2。模型采用六面体网格与楔形体网格均匀划分，因主要考虑软弱夹层对边坡稳定性的影响，为提高数值模拟的准确性，对软弱夹层区域的网格进行了加密。边坡网格模型见图3。

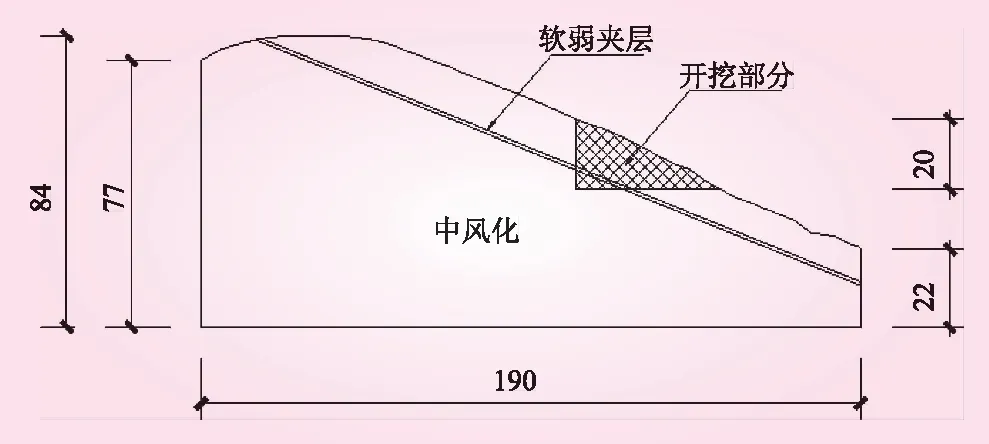
图2 简化边坡剖面(单位：m)

图3 边坡模型网格划分

2.3 有限元模型及其力学参数选取

基本假定：作用在含软弱夹层边坡上的外部荷载主要来源于研究区岩层的自重；分析过程不考虑构造应力带来的影响；岩体与软弱夹层岩性为各向同性且均匀的材料；含软弱夹层岩质边坡中软弱夹层与节理面密切接触，不发生脱离与滑动。

含软弱夹层的缓倾顺向岩体边坡发生失稳破坏时，破坏过程具有渐进性，软弱夹层往往具有应变软化效应。因此，对软弱夹层区域赋予强度参数随时步发生变化的应变软化模型，周围岩体采用摩尔-库仑模型。经地质演化分析可知，软弱夹层是坡体覆盖层红粘土经过雨水冲刷、入渗等各种地质作用发育而成，其粘聚力与内摩擦角会随等效塑性应变的不断增加逐渐降低至残余强度值，结合勘察报告以及GB/T 50218—2014《工程岩体分级标准》可得研究模型的计算参数，具体见表1。

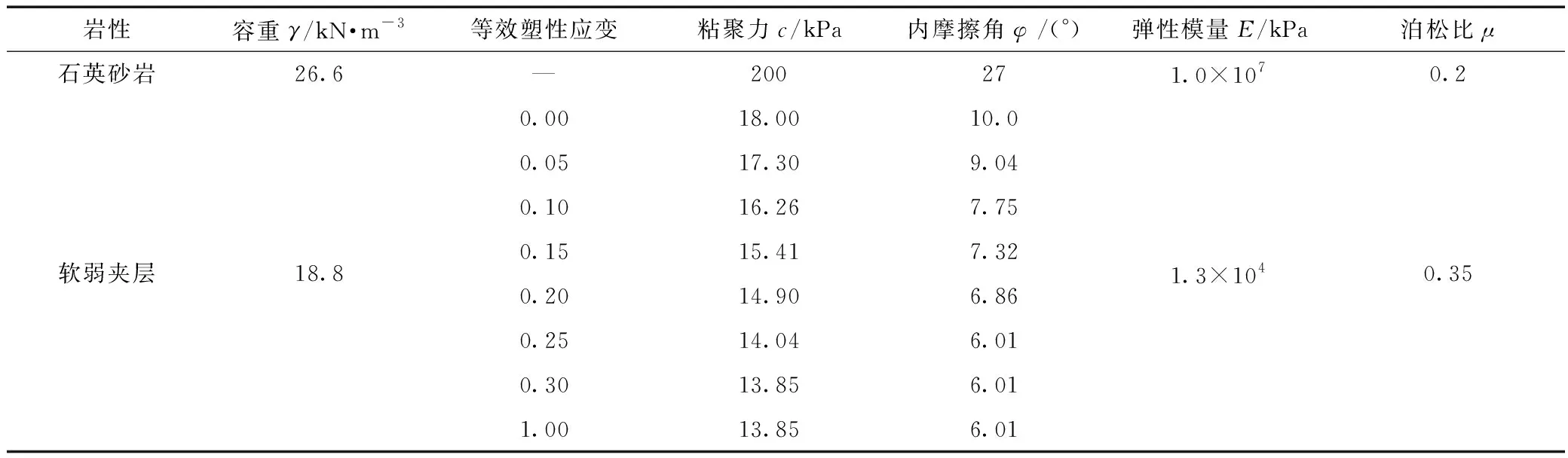
表1 力学参数

3 数值分析

3.1 边坡开挖完成后的稳定性研究

为保证边坡开挖后获得的数据准确有效，对边坡开挖前初始应力状态下的各方向上的位移及速度清零。为分析边坡开挖后的变形特征，沿边坡开挖临空面至坡顶在软弱夹层上等间距设置了5个监测点，在数值模拟过程中监测其各项变形特征，利用数据处理软件将其整理成图，从而获得边坡开挖后的真实变形破坏过程。监测点布置见图4。

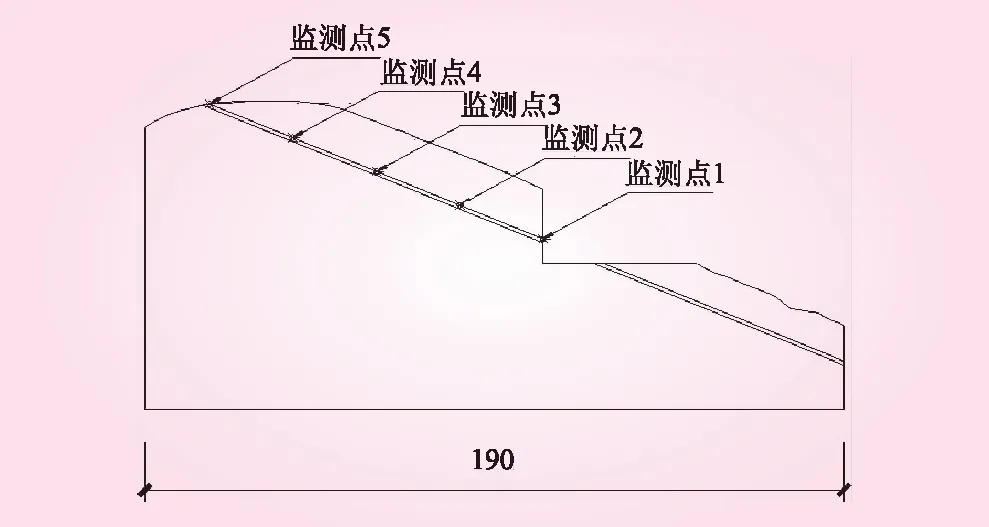
图4 边坡监测点示意(单位：m)

X方向位移云图见图5。从图5可知，边坡后缘处的位移仅有毫米级，而前缘值较大且最大可达2 m，在距临空面不远处产生了显著的位移突变。随着时效变形的不断积累，坡体将在位移突变处产生拉裂缝，最终在该处被拉断并沿软弱面发生滑移，属于滑移-拉裂破坏模式。

图5 X方向位移云图

剪应变增加速率云图见图6。从图6可知，边坡开挖后，剪应变增加速率在软弱夹层区域出现集中，边坡破坏时并没有全部贯通，而在边坡后缘停止发展。分析原因为：后缘软弱夹层上部岩体较少，虽然软弱夹层本身抗剪强度较低，但足以抵抗其上部岩体产生的下滑力。

由于研究对象的节点数和单元数较多，为提高效率，采用人工折减法计算。采用折减系数Fs=0.50、0.52对边坡原始强度参数进行折减。折减到0.50时，体系处于平衡状态；折减到0.52时，体系处于不平衡状态，说明边坡安全系数介于0.50～0.52之间，故取中间值0.51再次进行折减计算。边坡X方向速度历时见图7。从图7可以看出，折减系数取0.51时，X方向的速度趋近于0，说明边坡处于稳定状态。而折减系数取Fs=0.52时，X方向的速度突然迅速上升。由此可判断，此边坡的安全系数为0.51。

图6 剪应变增加速率云图

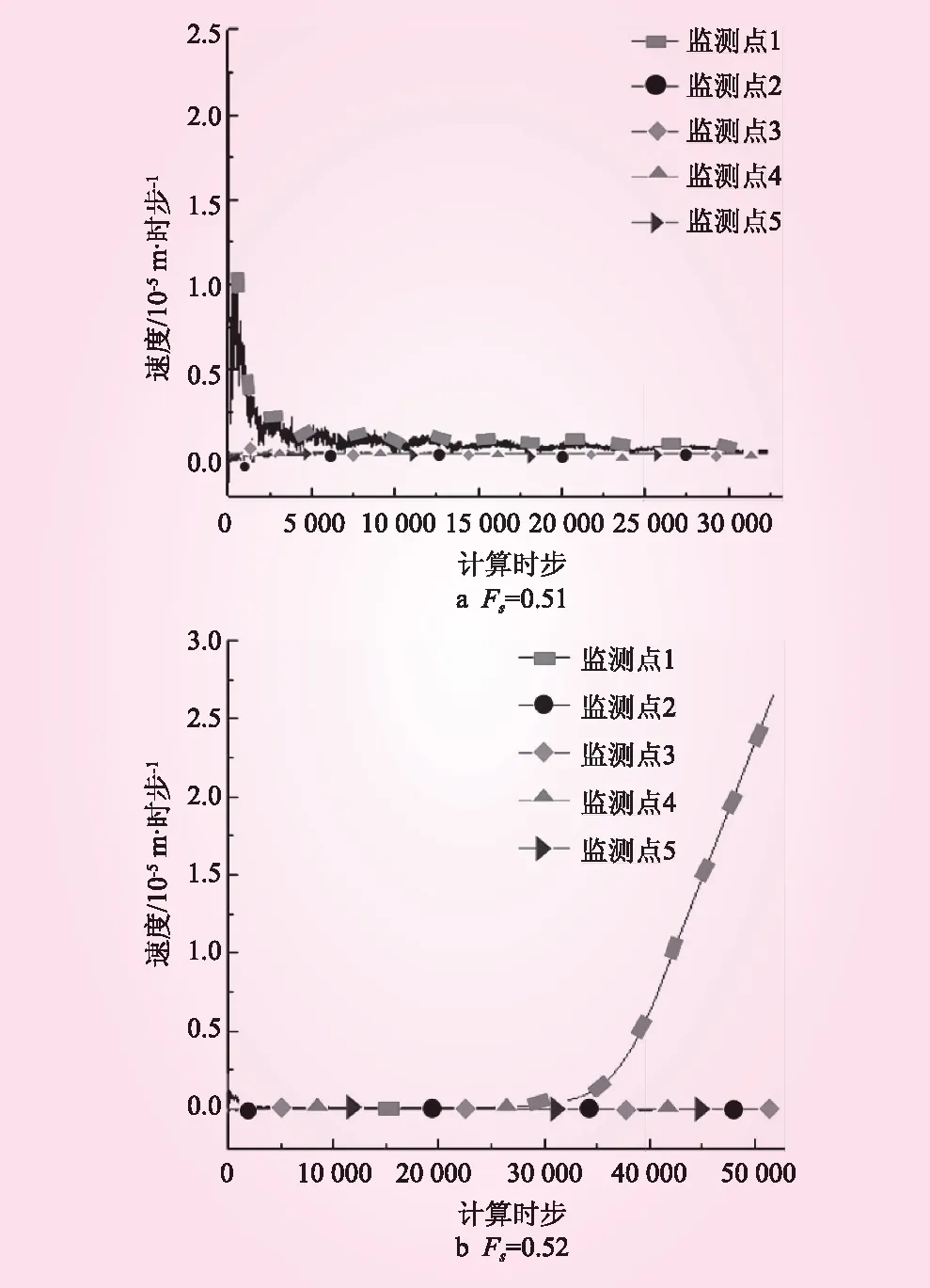
图7 X方向速度历时

X方向位移等值线云图见图8。从图8可知，边坡开挖卸荷后，坡体后缘会产生较大的位移差，位移差的存在诱发产生了拉张裂缝，随着时间的不断推移，裂缝逐渐发展至贯通，进而导致滑体与母岩脱离，最终沿着软弱夹层向临空面滑动。剪应力历时见图9。从图9可知，软弱夹层的剪应力峰值效应在滑面上随着滑体的蠕滑从边坡前缘向后缘不断传递，达到峰值强度后进入残余强度阶段，表明边坡的破坏具有时效性，从临空面至边坡后缘不断发展，总体表现为滑移-拉裂破坏。

图8 X方向位移等值线云图

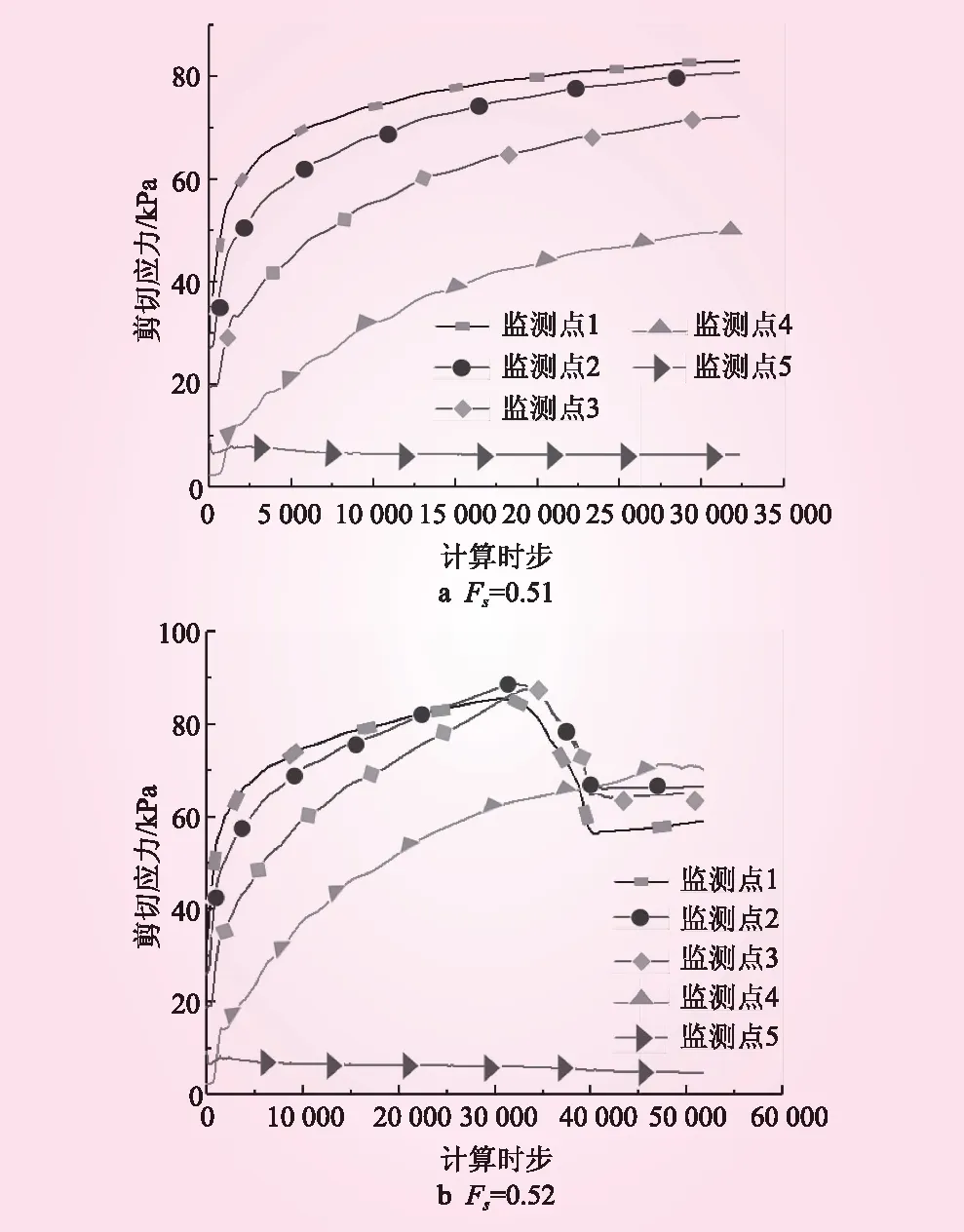
图9 剪应力历时

3.2 边坡渐进破坏分析

开挖N步时的剪应变增加速率云图见图10。开挖N步时X方向位移云图见图11。从图10、11可知，边坡开挖第1 000步时，在软弱夹层出露处有轻微的剪应变集中，此时临空面处软弱结构面上部滑体由于受剪而产生剪切位移。随着时间的推移，剪应变集中区不断向边坡后缘推进，且位移不断向后缘扩展，当达到25 684步时，软弱夹层剪应变集中区在滑面贯通，滑体变形从临空面逐步向坡顶发展，直至发生失稳破坏，表现为牵引式滑坡。

图10 开挖N步时的剪应变增加速率云图

图11 开挖N步时X方向位移云图

综上所述，缓倾顺向软弱夹层岩体边坡开挖卸荷后表现出明显的渐进破坏性。由于软弱夹层的强度参数明显低于周围岩体，其抗剪能力不足以抵抗上部岩体的下滑力，开挖卸荷后临空岩体失去下部岩体支挡，破坏率先在软弱夹层出露处发生。这种破坏是一个循序渐进的过程，并不是一蹴而就的，是从坡前缓慢向后缘逐步发展的结果。

3.3 强度参数对边坡稳定性的敏感性分析

采用控制变量法分别改变软弱夹层的粘聚力、内摩擦角，研究其中1个参数时，保持另1个参数值恒定。根据红粘土粘聚力c、内摩擦角φ常见值进行适当极端扩宽，采用线性差值获得相应变量值。安全系数变化见图12。从图12可知，采用极限平衡法比FLAC3D软件强度折减法的计算结果更保守且敏感性更低，边坡稳定性随抗剪强度的增大而增大；极限平衡法计算的安全系数与FLAC3D计算趋势是一致的，安全系数随内摩擦角的变化更加显著。可以得出，当边坡的高度和软弱夹层的几何参数(倾角、厚度、位置等)一定时，软弱夹层力学参数对边坡稳定性的敏感强弱为：内摩擦角φ>粘聚力c。

在软弱夹层内取一微元体进行受力分析。微元

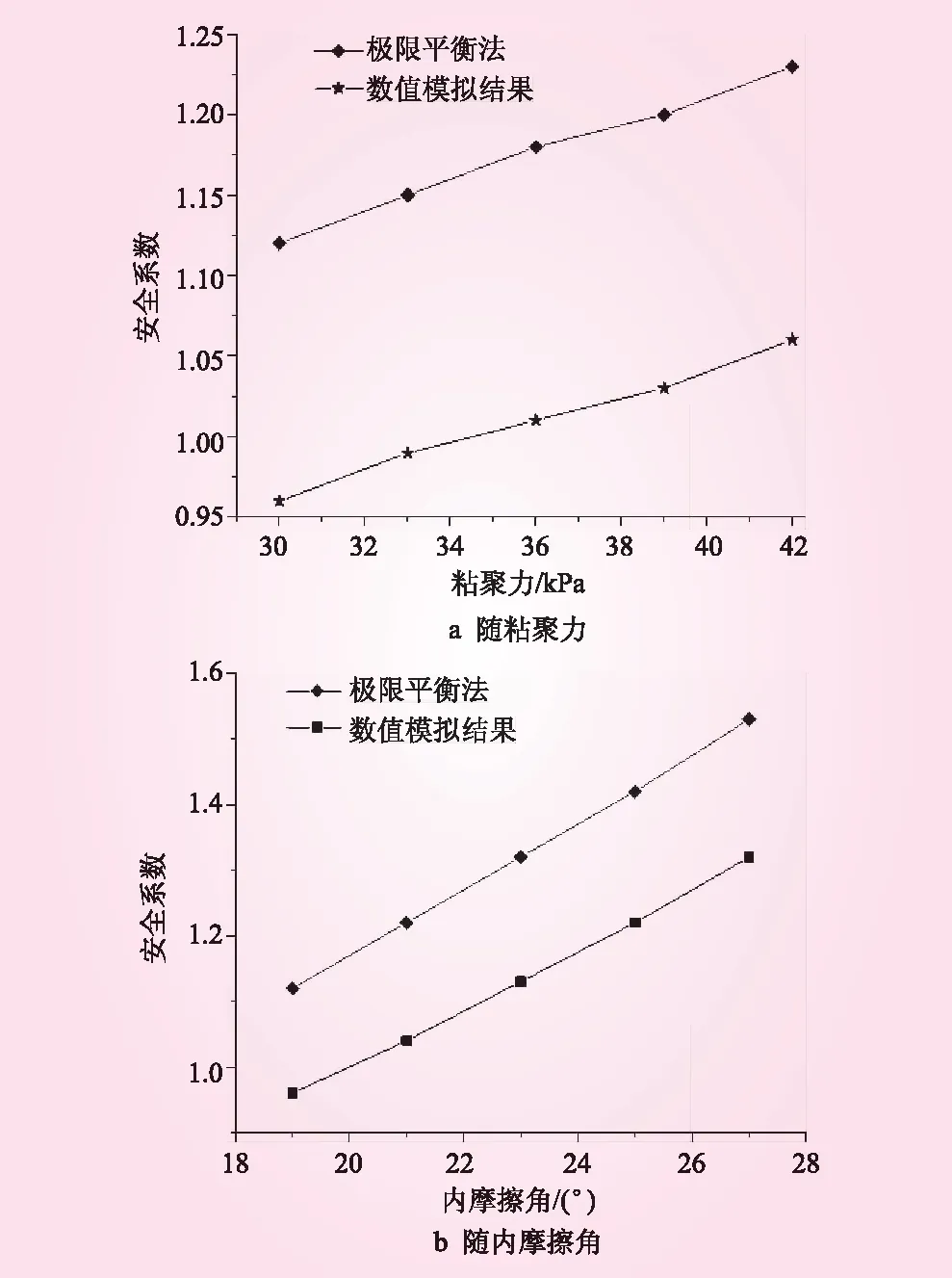
图12 安全系数变化

体在垂直纸面方向上所受法向正应力为σ2，则最大、最小主应力σ1、σ3必在平行于纸面所在平面内。以软弱夹层倾向方向为x轴，垂直软弱夹层方向为y轴建立直角坐标系。令σ3与x轴夹角为β，由弹塑性理论可知微元体的剪切破坏面为m-n面。根据前人研究可知，剪应力τ所在平面与最大主应力σ1作用面的夹角为45°+φ/2。由几何关系可知，剪应力τ所在平面与y轴夹角为45°+φ/2+β。将剪应力τ沿坐标轴分解为τx和τy，则软弱夹层上部潜在滑移体产生的下滑力由软弱夹层的∑τx为其提供抗滑力。微元体受力分析见图13。公式为

τ=c+tanφ=τsin(45°-φ/2+β)
=c+σtanφ)sin(45°-φ/2+β)

(2)

图13 微元体受力分析

当φ保持不变时，τx随粘聚力c的增大而增大。当c保持不变且φ在19°～27°时，由三角函数性质可知，σtanφ的影响远大于sin(45°-φ/2+β)，故τx也随内摩擦角φ的增大而增大。安全系数随抗剪强度变化的趋势符合预期且与前人研究成果相一致，进一步验证了上述观点。

4 结 语

本文基于有限差分FLAC3D软件，对缓倾顺向软弱夹层岩体边坡开挖卸荷后的稳定性进行分析，主要结论如下：

(1)含缓倾顺向软弱夹层岩体边坡的失稳破坏并不是一蹴而就的，而是一个时效变形过程，具有明显的渐进性。边坡经开挖卸荷后，坡体在软弱夹层出露处率先发生剪切屈服，不断发生蠕滑变形，并逐渐向后缘扩展，最后在坡体后缘处产生拉张裂缝并沿软弱夹层发生滑移-拉裂破坏。

(2)在软弱夹层常见强度参数范围内，极限平衡法计算得出的安全系数略大于1，边坡处于稳定和欠稳定状态，而在数值计算得出的安全系数却小于1，边坡处于失稳状态。由此可见，传统极限平衡法对此类边坡进行稳定性评价时可能夸大了边坡的安全性。因此，在对此类边坡进行稳定性分析时，有必要利用数值软件加以验证。

(3)当边坡的高度和软弱夹层的几何参数(倾角、厚度、位置等)一定时，软弱夹层力学参数对边坡稳定性的敏感强弱为：内摩擦角>粘聚力。