改进剑桥土蠕变模型分析
2019-03-15刘泽华
刘泽华,张 宇
(1.格拉斯哥大学 工程学院, 英国 苏格兰格拉斯哥市 G128QQ;2.大连理工大学 土木工程学院岩土工程研究所, 辽宁 大连 116024)
弹塑性模型是土力学中常用的本构模型,其中改进剑桥模型(Modified Cam-Clay),即MCC模型可以较简单实用地描述土体应力-应变特性,是最常用的弹塑性模型之一[1-3]。然而,改进剑桥模型在计算土体的应变时,仅仅取决于有效应力的增量大小而无法考虑时间效应,因此该模型不适合模拟土体蠕变以及依赖应变速率的岩土工程相关问题。
土体的蠕变特性会对工程结构物的稳定性造成影响,Mitchell等[4-5]的试验均表明土体的蠕变是引起比萨斜塔地基持续发生不均匀沉降的重要原因。此外,土体蠕变也是引起边坡失稳等地质灾害的重要因素之一[6-14]。引起土体蠕变的因素有很多,且蠕变的过程通常较为复杂。其中,土体不排水剪切强度和预固结压力的加载速率具有明显的时间依赖性,或表现出黏性行为。蠕变变形是不能忽视的土体特性之一。
本文基于黏弹塑性模型,在改进剑桥模型基础上提出可以考虑土体蠕变特性的改进剑桥土蠕变模型(Modified Cam-Clay Creep),即MCCC模型。应用MCCC模型模拟了三轴试验的试验结果,验证了该模型模拟土体典型受力条件下的可靠性;通过与MCC模型进行对比,讨论了MCCC模型的不同与优点。
1 理 论
本文试验采用传统的三轴试验。三轴试验可以完善的测试排水和不排水剪切条件下土体的应力-应变响应。在模拟三轴试验中各加载条件下土体响应问题时,MCC模型的有效性已经被验证[15]。三轴实验的土体参数以及试验的初始状态列于表1中。

表1 土体性质参数和初始状态
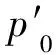
1.1 各向同性加载
1.1.1 MCC模型
根据MCC模型,当土体受力状态未达到屈服线时,土体处于弹性变形阶段,仅发生弹性应变,此时土体的应变可按下式计算。
(1)
(2)
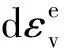
土体的屈服曲线可以表达为
(3)
模型采取硬化准则
(4)
式中:λ为土体的压缩系数。
以及流动法则
(5)
式中:η为应力比。
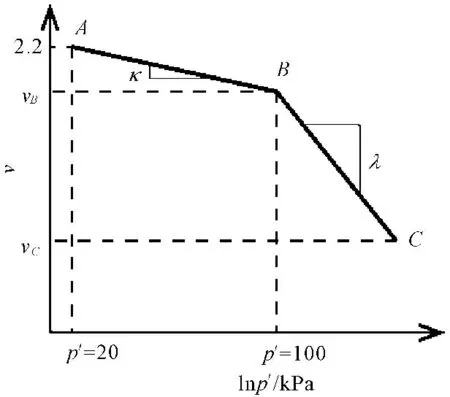
土体的初始状态在表1中给出,如图1所示,在A点,土体平均有效应力p′=20 kPa、土体的比容(单位质量土体的体积)v=2.2。根据MCC模型,可以计算得到,当p′增大至1 000 kPa时(C点),v=1.659。
1.1.2 MCCC模型
为了考虑加载的时间效应,在施加在土体上的有效应力的表达式中引入加载速率项,用系数K来表示荷载加载速率的快慢,即
(6)
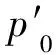
(7)
上式通过系数K可以考虑荷载以一定的速率增加,在一定时间增量内,对应的荷载增量引起土体的黏塑性比容变化(dvvp)可以按下式计算
(8)
(9)

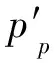
(10)
dv=dvvp+dve
(11)
(12)
在各向同性条件下,分别计算模拟了平均有效应力p′从20 kPa瞬间增加到50 kPa、100 kPa、200 kPa,然后保持恒定这三种工况。
1.2 排水剪切
1.2.1 应力控制下的MCC模型

(13)
式中:q为土体的偏应力。

(14)
(15)
1.2.2 应力控制条件下的MCCC模型
1.2.3 应变控制条件下的MCCC模型
在应变控制条件下,给定施加的剪切应变增量dε/dt,控制时间步长尽可能小,然后根据时间增量,计算黏塑性比容应变。
1.3 不排水剪切
1.3.1 MCC模型


1.3.2 MCCC模型
与排水条件下的MCCC模型类似,在给定的应力增量或应变增量加载速率下,对土体的各参数的增量进行计算,值得注意的是,在不排水条件下,土体的总比容保持不变,而孔隙水压力则可以通过土体平均有效应力的增量进行计算。
2 模拟结果
2.1 各向同性加载
图2给出了根据MCC模型计算得到土体压缩曲线,以及根据MCCC模型计算得到的在不同荷载加载速率下的土体压缩曲线。其中,两种模型计算的初始荷载相同;MCCC模型中,分别计算了荷载加载速率K为0.1 kPa/d、1 kPa/d、10 kPa/d。
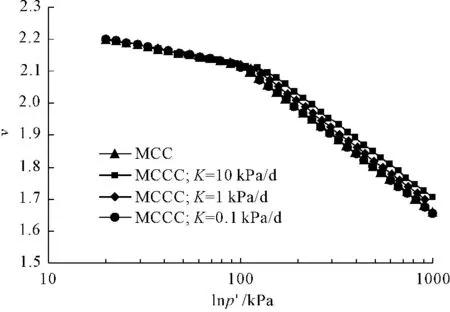
观察图2可以发现,MCCC模型和MCC模型的计算结果整体上趋势一致,其中,当荷载加载速率为0.1 kPa/d时,MCCC模型的计算结果与MCC模型结果基本重合。在荷载施加初始阶段,4条曲线基本没有差别。当荷载增加至100 kPa后,4条曲线出现差异。对于MCC模型计算结果,当荷载增加至100 kPa时,土体开始发生塑性应变,因此土体的比容变化斜率增大。而MCCC模型在开始时考虑土体有塑性应变,这意味着当施加载荷时,在开始时即存在弹性和塑性应变,因此在达到屈服荷载后,MCCC模型的计算结果会与MCC出现明显差异,且随着荷载施加速率的增加,两种模型计算结果的差异越大。
从图2还可以发现,MCC和MCCC模型之间的趋势是相同的。另外,他们是彼此平行的。因此,当土体的密度增加(空隙率降低和垂直有效应力常数)时,相同的蠕变变形量需要更长的时间。
图3给出了根据MCCC模型计算得到的在各向同性载荷下提高平均有效应力p′后,土体比容与时间对数ln(t)之间的关系。从图3可以看出,MCCC模型可以描述土体比容随时间的变化,即可以描述土体的蠕变效应。需要注意的是,在本算例计算过程中,由于本次模拟的加载总时间为106 d,计算时间步长为10-4d。
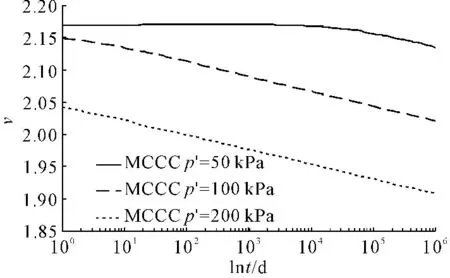
从图3可以看到,荷载的大小对土体的蠕变有重要影响。荷载越大,土体比容开始发生变化的时间越早,而在计算结束时发生的比容变化总量也越大。当荷载为50 kPa时,土体比容首先保持稳定,在荷载施加10 000 d后,土体比容开始下降;而荷载为100 kPa和200 kPa时,土体比容则在荷载施加之后迅速发生变化。
2.2 排水剪切
图4—图7为根据MCC模型和MCCC模型对应力控制加载条件土体排水剪切的模拟结果。
如图4所示,4条曲线的应力路径相同,最终达到临界状态线(CSL),这是因为MCCC模型和MCC模型均采用了方程δp′=δq/3。

图4 排水条件下荷载加载速度土体应力路径的影响

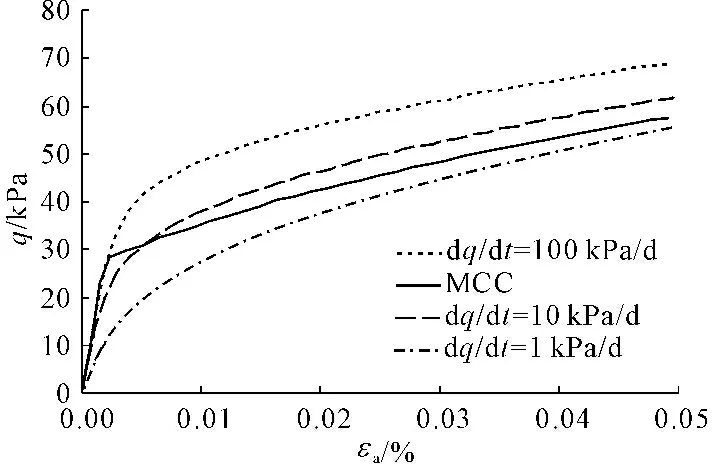
图6 排水条件下荷载加载速度对土体偏应力随轴向应变曲线的影响

图5和图6分别给出了在应力控制加载条件下,MCC模型计算得到的土体比容、以及q与轴向应变的关系曲线,以及在不同荷载加载速率下根据MCCC模型计算得到的土体比容与轴向应变的关系曲线。观察图5和图6可以发现,随着荷载加载速率的增大,MCCC模型计算得到的土体比容随轴向应变的变化率逐渐变小,q随轴向应变的变化斜率则逐渐增大。而MCC模型计算得到的土体比容、以及q随轴向应变的变化率介于荷载加载速率为1 kPa/d和10 kPa/d之间。
图7给出了应变控制加载条件下,土体比容与轴向应变的关系曲线。总体来讲,当轴向应变增加时,土体比容减小;土体刚度随着应变率的提高而增加但是,MCCC模型和MCC模型计算结果的趋势在结束时趋于相同,即此时当轴向应变继续增加时,两种模型计算得到的土体比容不会进一步减小。图8给出了应变控制条件下,土体荷载随轴向应变的关系曲线。当应变率较高时,土体刚度和屈服应力会更高。在屈服面上,MCC模型和MCCC模型计算结果的趋势没有太大差异,因为此时土体的塑性应变很小。
2.3 不排水剪切
图9至图11给出了MCC模型和MCCC模型计算得到的土体在应力控制条件下、不排水剪切试验的模拟结果。


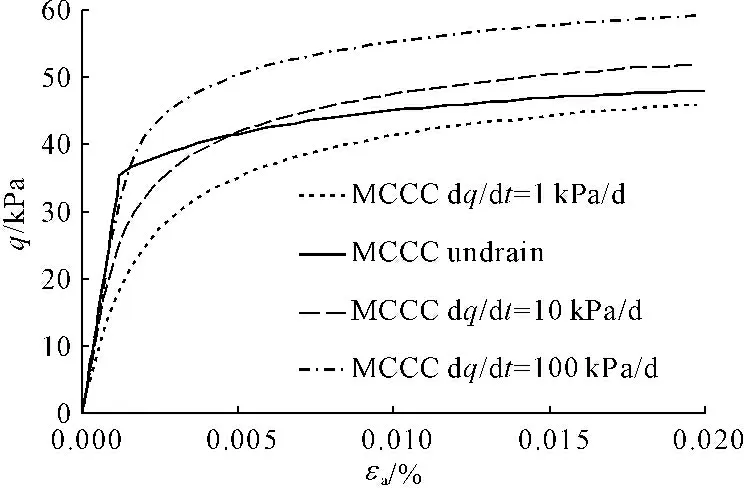

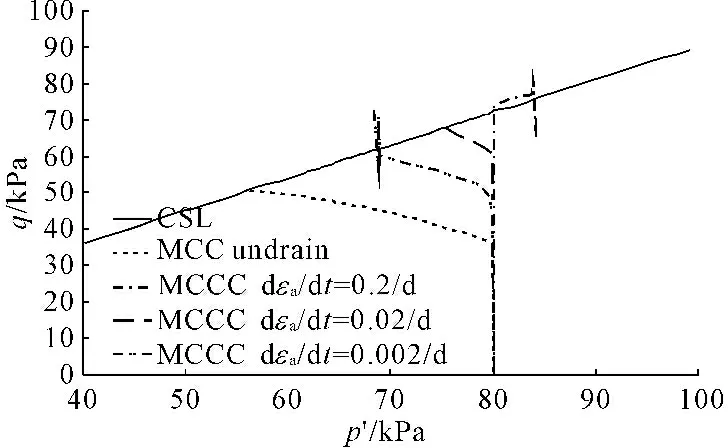
图9为土体应力路径曲线。由MCC模型计算结果可见,在土体没有达到屈服应力之前,p′维持在80 kPa没有变化;继续加载,p′会逐渐减小。相比之下,MCCC模型计算结果显示,土体在荷载开始加载后,由于黏塑性一直发生,p′就逐渐开始减小,p′的减小速度随着荷载施加速率的增大而减小。最终,4条曲线均达到CSL线上。值得注意的是,MCCC模型在到达CSL线之前,p′是减小的;在超过CSL线之后,p′有所增大,并最终到达CSL线,这意味着此阶段土体的塑性变形为负,且弹性应变为正值。
图10为施加荷载与土体轴向应变关系曲线,图11为土体孔隙水压力随轴向应变的关系曲线。整体上,MCCC模型和MCC模型计算结果的趋势是一致的。随着荷载施加速率的增大,q随轴向应变的变化斜率也增大,而孔隙水压力随轴向应变变化的斜率则会减小。
图12和图13分别给出了在应变控制加载模式下,不排水剪切条件下土体应力路径以及土体所受荷载随轴向应变的变化曲线。由图13可知,土体达到屈服点的速度随着荷载施加速度增大而减慢。图12则表明,当应变施加速率为0.2/day时,MCCC模型计算结果显示,土体的p′基本保持不变,将指向CSL线;随着应变加载速度的减小,达到CSL线时土体的p′越小。

3 结 论
MCC模型是一种用于描述土体特性的简单方法,该模型假设塑性应变仅在屈服后出现,当土体达到屈服时,土体的刚度将急剧变化。本文提出的MCCC模型是在MCC模型的基础上,假设土体在荷载作用下的任何阶段均有塑性变形,且考虑荷载施加速度的大小,从而使该模型可以描述土体的蠕变特性。通过与MCC模型的比较,可以得到MCCC模型具有如下几点优势:
(1) MCCC模型可以模拟土体参数的时间依赖性。
(2) 当土体受到的有效应力恒定时,MCCC模型可以描述土的蠕变行为。
(3) 在排水剪切条件下,当轴向应变增大时,土体比容减小,且偏应力增大。
(4) 在不排水剪切条件下,应变加载的模拟结果显示,当轴向应变增加时,土体的偏应力和孔隙压力均增加;应变控制加载的模拟结果显示,当轴向应变增加时,土体的偏应力增加,但是在土体应力状态达到CSL线之前,土体的孔隙水压力减小,土体应力达到CSL线后,孔隙水压力增大。
(5) 土体的屈服应力随着剪切速率的增加而增加。
需要指出的是,通过与MCC模型对比分析,MCCC模型具有描述土体蠕变行为的一种简单的计算模型,但仍需要相关的试验验证,以及对MCCC模型参数的修正。
