某砂岩型铀矿钻孔中镭氡平衡系数的数值模拟

洪 昆，杨亚新，罗齐彬，何辉龙，肖 昆，王帅帅，符志军

（1.东华理工大学地球物理与测控技术学院， 南昌 330013；2.核资源与环境国家重点实验室，南昌330013；3.湖北省核工业地质局，湖北 孝感 432100）

二十世纪九十年代以来， 我国铀矿勘查重点已由硬岩型铀矿转移到了低品位、 经济可采的地浸砂岩型铀矿［1］。在可地浸砂岩型铀矿钻探勘查过程中， 钻孔穿透矿层后， 矿层上下隔水层被破坏， 由于泥浆循环时压力与地层压力不同， 砂岩孔隙度较发育， 连通性较好， 导致溶解在地下水中的氡发生迁移，这一现象称为 “压氡现象”［2］。钻进过程中由于压氡现象的存在， 泥浆的配比， 井孔壁附着的泥浆饼等， 都会对伽马射线产生吸收或屏蔽作用，影响铀含量估算。

γ 测井测量的γ 射线特征能量为1.785 MeV，主要是214Bi 的贡献， 而铀系中主要的伽马射线来自镭组氡的子体214Bi 和214Pb［3］。为保证伽马测井结果的准确性， 只有当铀镭氡处于平衡状态时， 矿层铀含量才能由测井结果反映出来。 钻探过程中由于原地层被破坏， 氡会随之迁移， 镭氡平衡发生位移， 氡的迁移导致214Bi 特征能量变化， 不能与平衡铀系的射线强度对应， 测井结果不准确。 因此， 伽马测井时镭氡放射性平衡显得尤为重要［4］。

在实际伽马测井中， 只有铀镭氡处于放射性平衡状态时，FD-3019 伽马测井仪才能准确地换算伽马射线含量与强度的关系。 研究地层中铀镭氡平衡情况时， 获得铀镭平衡系数和镭氡平衡系数才能准确定铀含量。 铀镭的半衰期分别为4.468×109a，1 600 a，钻进时间一般较短， 可忽略铀镭的衰变量， 认为铀镭处于平衡状态［5］，而此时，影响伽马测井的主要因素则为镭氡平衡系数。

砂岩型铀矿勘查及开采过程中， 由于砂岩比较松散， 有效的岩心采取率一般不高，用传统矿段分析结果与伽马测井解释结果对比确定Ra-Rn 平衡系数的方法［6］，其结果误差较大， 笔者以某砂岩型铀矿为研究对象，利用放射性地球物理测井长期观测资料， 钻孔岩心样品数据等［7］，用数值模拟的方法综合确定Ra-Rn 平衡系数。

1 氡的特性和数值模拟基础

实际工作中， 一般采用物探参数孔来长期观测镭氡平衡的状态， 将初始的总照射量率与最后一次趋于稳定总照射量率比值作为镭氡平衡修正系数。 矿层被揭穿后， 氡气体会发生迁移， 一部分由于压氡现象发生对流扩散， 另一部分随循环液抽出到地表。 在压力和浓度梯度下氡往钻孔中迁移， 在时间尺度上表示为氡浓度逐渐上升并最后趋于稳定，与实际用照射量率计算镭氡平衡系数， 照射量率随时间逐渐变大并逐渐趋于稳定变化趋势相同， 模拟氡自钻孔被揭穿后的一系列运移过程获得镭氡平衡的信息， 可建立适当的模型运用数值模拟的方法研究这一过程， 并确定其影响因素。

1.1 氡的衰变规律

母核与衰变子体连续进行的衰变过程，通常称为连续（递次）衰变，铀衰变链中238U 经过一系列衰变变成226Ra，镭继续衰变成222Rn，直至衰变成稳定元素206Pb， 当母体核素的半衰期远远大于子体核素时， 能建立起长期平衡状态，放射性核素衰变服从指数衰减规律，此时放射性衰变变化可表示为：

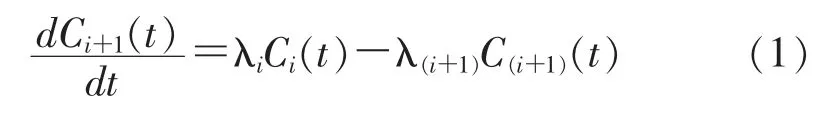
式中：i—第i 个核素，i ＝1，2，...；λ—衰变常数，s-1。

1.2 氡的迁移微分方程

氡气（特指222Rn）是具有衰变特性的放射性气体， 不同于氧气氮气等常规气体， 在短距离多孔介质中具有极强的迁移能力［8-10］均匀介质中氡气运移与分布的二维微分方程表示为：

式中：C—介质中氡浓度，Bq/m3；A—在单位体积单位时间内产生自由移动的氡的能力，Bq/（m3s）；λ—氡衰变常数，s-1；v—氡对流速度，m/s；n—介质有效孔隙度，无量纲；D—氡气的有效扩散系数，m2/s。

为得到任一微元体中氡运移的一般微分方程，用拉普拉斯算符Δ 和哈米尔顿算符▽简化，为：

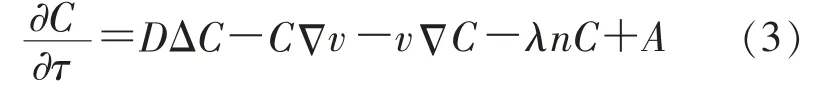
引入一个通用变量（特征变量）φ，可统一写成通用变量方程：

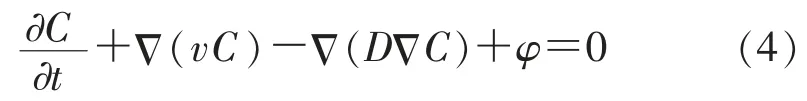
式中φ 为化学反应， 衰变吸附等引起的源汇项， 给定其初始条件和边界条件后可解出此偏微分方程，并获得氡的瞬态分布情况。

2 镭氡平衡系数的数值模拟

2.1 数值模拟控制方程和模拟边界条件

模拟计算时， 假设模型的孔隙度均匀分布， 氡各向同性扩散， 扩散速度相同， 氡对流作用主要在矿层区域， 忽略热量交换对氡迁移的影响， 边界稳定， 设置好初始条件和边界条件， 对模型进行网格化， 选择好时间和步长，开始计算。

数值模拟控制方程如下：

1）流体运移［11］考虑饱和多孔介质中的运移，用达西定律表示为：

式中：Q—质量流，kg·m-3·s-1；t—时间，s；ε—介质孔隙度；v—达西流速，m·s-1。

2）物质运移的控制方程由（4）变化为：

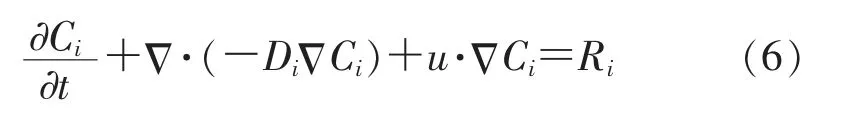
式中Ri表示源汇项，放射性物质物化反应导致源汇变化主要来源于其本身放射性衰变及孔隙壁面与流体溶质存在吸附作用。

3）Ra 的衰变方程：

将物探参数孔模型简化成3 层二维模型（图1）。 模拟物探参数孔将无限长层状的地层划分成一个二维模型，长为60.09 m，宽为20 m，在模型中心位置为钻孔， 钻孔的直径为0.09 m，上层覆盖层厚度6 m，中部为含矿砂岩，厚度为8 m，下层隔水底板底层，厚度为6 m。

图1 数值模型示意图Fig.1 Schematic diagram of numerical model

2.2 理想系统中镭氡平衡的模拟

建立一个理想封闭模型，将（封闭模型）视为理想混合系统，模拟理想情况下镭源的衰变情况，仅仅考虑镭衰变后产生氡以及氡自身的衰变（表1），观察理想封闭系统中镭的衰变情况。

将镭氡衰变系数代入到Ra 衰变方程，模拟封闭理想系统中镭自然衰变的情况。

模拟结果如图2 所示， 当氡全部由镭源产生时， 镭浓度变化很小， 可把镭当做稳定源，氡浓度在40 d 左右不变，镭氡平衡建立。

表1 模拟参数Table 1 Simulation parameter

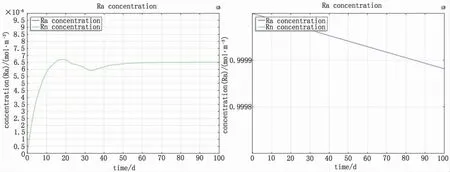
图2 理想封闭系统中镭氡平衡的模拟Fig.2 Simulation of radium-radon equilibrium in an ideal closed system

2.3 氡的迁移模拟

利用达西定律和物质传递耦合模拟氡的迁移， 达西定律可用来模拟饱和流体的低速流动问题， 当多孔介质渗透率小或孔隙度不大时［12-13］，流体在压力驱动下运移，流体主要受粘滞力的影响。

稀物质传递用来计算溶解在流体中的溶质运移［14］，物质传递满足Fick 定律，并在扩散对流机制下向前推进， 能求解溶解在流体中的物质的传递和反应， 获得物质在不同时间的分布状态。 数值计算模型中所用参数见表2。

3 结果分析

3.1 计算结果分析

观测氡从矿层产生， 在矿层中迁移到围岩及钻孔中的瞬态过程， 模拟得到氡迁移的时空间上的氡浓度分布， 分析研究氡的迁移对镭氡平衡的影响（图3）。

模拟刚开始时， 镭衰变产生氡， 镭衰变系数较小， 衰变产生氡较少， 氡不断累积，累积到一定程度时， 由于浓度差异开始向前迁移， 氡呈扇形向外运移， 迁移过程连续，主要表现在水平方向上， 垂向上氡的迁移量很小， 覆盖层氡浓度很低， 迁移的氡的数目与矿层相比小的多， 这与实际测量的照射量率数据相符合。 在浓度梯度和压力梯度下，氡在钻孔中累积， 钻孔中氡浓度逐渐上升，并在40 d 左右时氡浓度变化量很小，这与实际测量相符。

表2 数值模拟所用参数［15-17］Table 2 Parameters for numerical simulation［15-17］

图3 氡在矿层及围岩中的迁移Fig.3 Migration of radon in ore bed and hosting rock

图4 流线和压力分布图Fig.4 Streamline and pressure profile

图4 中， 压力表现为边界上压力高， 钻孔中压力低， 流线图中， 氡迁移时矿层中迁移速度较大， 覆盖层中迁移速度较小， 且水平的迁移速度比垂向迁移速度大得多， 钻孔中流动速度加快， 流体在钻孔出口位置速度较大，在矿层和覆盖层中流动速度较小。

设置监测点， 监测钻孔中氡浓度随时间变化趋势图， 横向上取不同间距的各点，（矿层中央位置）以5 m 每个点向前设置，观察横向上各点及钻孔中平均氡浓度随时间的变化趋势（图5）。

3.2 结果对比分析

图5 横向上监测点的设置Fig.5 Setting of horizontal monitoring points

为了验证利用氡浓度计算镭氡平衡系数的数值模拟方法， 用物探参数孔法计算镭氡平衡系数和矿心分析与γ 测井解释结果计算镭氡平衡系数对比分析。

1） 镭氡平衡被破坏到再次达到镭氡平衡，需经过氡的10 个半衰期左右［18］。将观测铀矿段恢复前后的实际测量值的比值作为物探参数孔法镭氡平衡系数修正值。

2）根据矿心镭含量分析结果与γ 测井解释镭含量结果计算镭氡平衡系数［19］。两种方法计算得到镭氡平衡系数见表3。

通过物探孔参数测量法和矿心分析与γ测井解释结果计算的确定方法计算得出的镭氡平衡系数。 物探孔参数测量法计算的镭氡平衡系数PRn＝0.842，受客观因素影响小，但成本较高，周期较长。γ 测井解释结果计算的镭氡平衡系数PRn＝0.956，在计算过程中采用对采取率修正的办法， 但无论怎样修正， 必然存在用高品位结果代替低品位或者用低品位代替高品位的情况， 对镭氡平衡系数计算结果都会产生一定的误差。

钻孔中平均氡浓度随时间变化如图6，可通过氡的浓度与时间变化曲线观察镭氡是否平衡， 矿层中氡持续累积， 到镭氡平衡重新建立后， 体现为矿层及钻孔中氡浓度趋于稳定， 钻孔中氡浓度随时间的变化量就很小并趋于矿层中氡浓度。 与实际照射量率相比两者增长趋势相似， 因此可通过氡的浓度与时间的变化曲线来判断镭氡之间是否达到平衡状态并给出镭氡平衡修正系数。 将氡累积并不会发生变化的浓度当作稳定浓度，40 d 后重新达到镭氡平衡的饱和氡浓度作为修正的分子， 用镭氡平衡后稳定的氡浓度和平衡被破坏前饱和的氡浓度作为镭氡平衡系数修正值，砂岩中射气系数取K＝0.31。

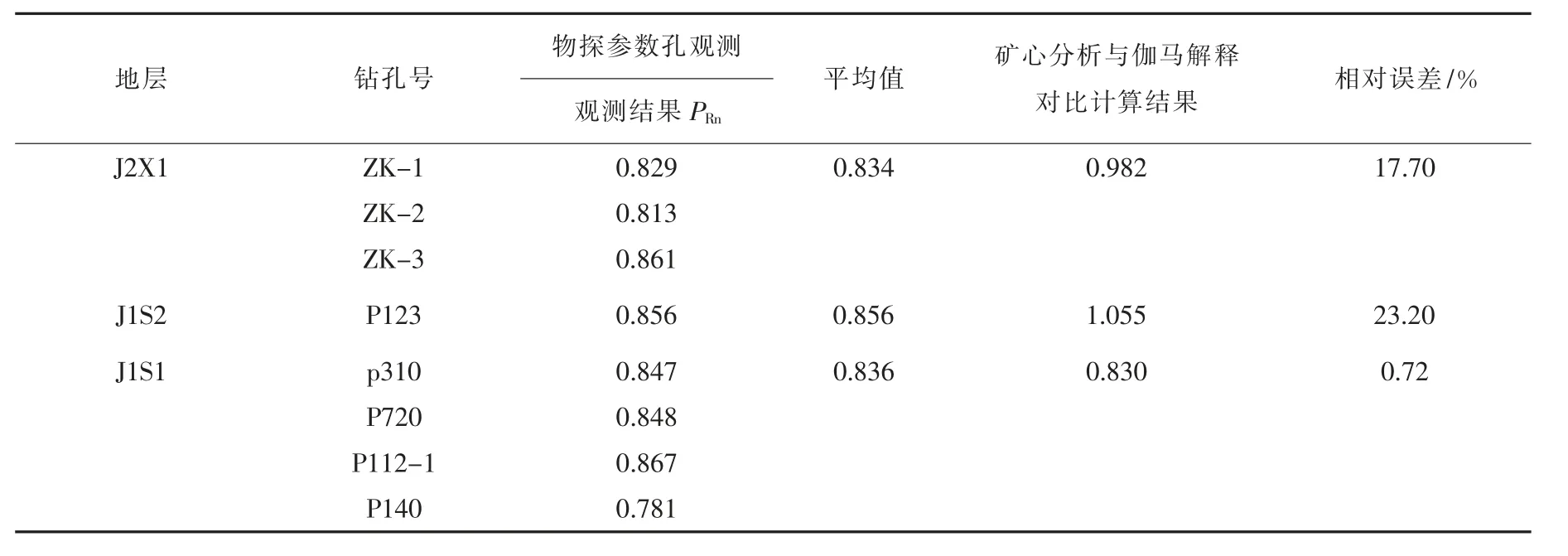
表3 物探参数孔观测结果与矿段分析γ 解释计算结果对比表Table 1 Comparison of borehole observation results by geophysical parameters and γ calculated interpretation results of analysis-ore segment

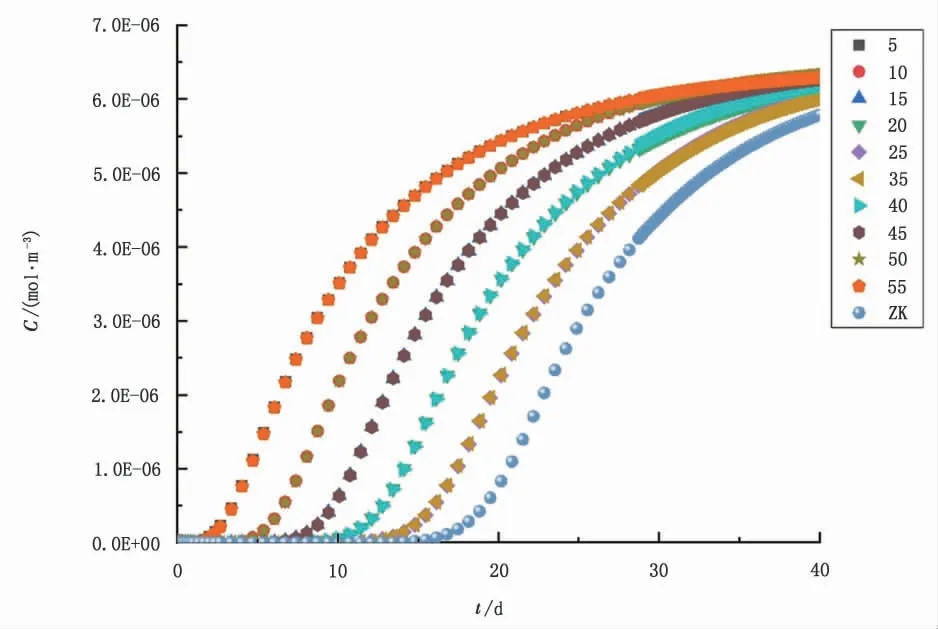
图6 钻孔中平均氡浓度随时间变化趋势图Fig.6 Trend chart of average radon concentration in borehole with time

4 结论

通过数值模拟计算， 模拟氡在矿层及围岩中的运移， 分析氡浓度在模型时间和空间上的分布，得到以下结论：

1）镭衰变产生氡，氡逐渐积累，在浓度梯度和压力梯度下， 氡开始向前迁移， 氡从边界向钻孔中迁移过程连续，迁移速度较慢，主要表现在水平方向上， 垂向上氡的迁移量很小， 上下两层的迁移的数目与矿层的相比要小得多， 这与实际测量得到数据具有相同的特点。

2）氡浓度与时间的变化曲线与实际测量的伽马照射量率与时间的关系曲线中， 两者具有明显的相似性， 将氡累积并不会发生变化的浓度当作稳定浓度，40 d 后重新达到镭氡平衡的饱和氡浓度作为修正的分子， 用镭氡平衡后稳定的氡浓度和平衡被破坏前饱和的氡浓度比值作为镭氡平衡系数修正值， 计算得到镭氡平衡系数系数PRn＝0.890。