改进关联规则算法对乳腺癌扩散的预测研究
2020-08-10艾云昊杨超宇李慧宗
艾云昊,杨超宇,李慧宗
(安徽理工大学,安徽淮南232001)
0 引言
乳腺癌是发生在乳腺上皮组织的恶性肿瘤,原位的乳腺癌并不致命,但是由于乳腺癌细胞丧失了正常细胞的特性,细胞之间连接松散、容易脱落,一旦癌细胞脱落,游离的癌细胞就会随着血液或淋巴液扩散至全身,形成转移,危及患者的生命。根据2019年1月国家癌症中心发布的全国癌症统计数据,乳腺癌是女性中发病率和死亡率最高的癌症[1]。因此,寻找出关联度高的因素,并利用这些因素对乳腺癌的扩散进行预测具有十分重要的意义。
关联规则的概念最早由Agrawal[2]于1993年提出,目的是用来解决顾客交易数据库中的关联规则问题。由于当时用来进行关联规则挖掘的AIS算法在运算过程中会产生过多的候选项集,在1994年Agrawal和Srikant根据AIS算法提出了Apriori算法[3],这种布尔型关联规则挖掘频繁项集的算法能大大提高数据挖掘的效率。但是算法在实际应用中存在一些缺点,其中之一就是此算法只能处理离散数值而无法处理连续数据。针对该问题,传统的方法是通过直接划分将连续数据转换为若干离散区间。不过,这种离散化手段存在“尖锐边界”问题。1995年,Cubero等[4]引入模糊集理论,提出“模糊关联规则”,之后陆续有学者从隶属度函数的确定[5]和模糊关联规则模型的构建[6]等方面对模糊关联规则进行了研究。
本文将从支持度的计算方法入手,提出根据模糊区域分别计算事务项支持度的计算方法,这项改进使得Apriori算法能够处理的数据不仅仅只限于离散型数据。改进算法还引入了确定性因子(certainty factor,CF)[7-8]以完善传统关联规则采用的“支持度-置信度”评价体系。对比改进算法和Apriori算法挖掘出的关联规则的数量和规则质量评价函数值[9],可知改进算法可以挖掘出更多的规则且挖掘出的规则质量更高,并且改进算法挖掘出的关联规则对乳腺癌患者临床治疗有一定的参考意义。
1 Apriori算法
Apriori算法是经典的布尔型关联规则挖掘算法,被广泛应用于数据挖掘领域。Apriori算法采用逐层搜索的迭代方法,利用先验知识进行候选项集剪枝,缩小搜索范围,挖掘算法步骤如下:
1)设定最小支持度minSupp和最小置信度minConf的阈值;
2)对数据库进行扫描,记录各项及其出现的次数得到候选1-项集,选取大于minSupp的项,组成频繁1-项集;
3)将频繁1-项集中任意两个项集彼此连接得到候选2-项集,对候选2-项集进行支持度的计算,然后保留满足支持度值的项集,得到频繁2-项集;
4)以此类推,将频繁(k-1)-项集中任意两个项集彼此连接得到候选k-项集,然后对候选k-项集进行支持度的计算,保留大于minSupp的项,组成频繁k-项集。重复该步骤,直到候选N-项集的所有项的支持度都小于minSupp为止,此时频繁(N-1)-项集就被称为最大频繁项集;
5)获取最大频繁项集的非空子集,计算各个非空子集之间的置信度,选出大于minConf的规则,这些规则就是强关联规则。
2 引入模糊集理论的改进Apriori算法
2.1 连续型数据支持度的计算
本文考虑的情况是数据中只有一个属性的数据是连续型数据的情况,运行Apriori算法时只需改变对连续型数据的支持度计算方法即可。具体步骤如下,假设数据中只有一个属性的数据是连续型数据,首先确定隶属度函数,根据隶属度函数对原始数据进行模糊化,将模糊属性分为N个模糊区域(X1,X2,…,XN),然后将数据库内的每一个项Zi分为T=((Zi,Y1),(Zi,Y2),…,(Zi,YN))这N种情况。假设N为3,对候选项T进行计数时,先对数据库进行扫描。假设一条事务内同时含 有Zi和 连 续 数 据Y,先 将Zi分 为(Zi,Y1)、(Zi,Y2)、(Zi,Y3)这3种 情 况,它 们 的 支 持 度 为S1、S2、S3。计 算 连 续 数 据Y在(X1,X2,X3)这3个 模 糊 区 域 上 面 的 隶 属 度f1、f2、f3,然 后S1、S2、S3分别加上f1、f2、f3。若某一条事务中只含有Zi不含有连续数据Y,则对S1、S2、S3分别加上1/N(这里假设N为3,所以是分别加上1/3),以此类推。最后将S1、S2、S3分别除以总事务数D就得到了(Zi,Y1)、(Zi,Y2)、(Zi,Y3)的支持度。
2.2 引入新指标
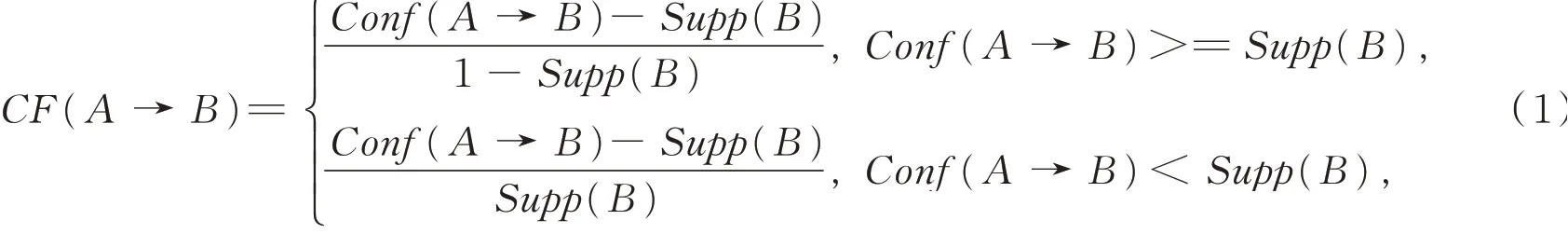
本文引入两个新的指标:①确定性因子(certainty factor,CF);②规则质量评价函数φ(r)。确定性因子CF(A→B)定义[7]为式中A→B为一条关联规则,A为前件,B为后件,Conf(A→B)为前件为A后件为B的关联规则的置信度,Supp(B)为关联规则后件B的支持度。由(1)式可知,确定性因子会产生一个[-1,1]区间的值。当得知A包含在某个事务中,确定性因子可以度量B在那个事务中的可信度是如何变化的。正值表示可信度增加,负值表示可信度下降,而0表示可信度没有变化。“支持度-置信度”评价体系加入确定性因子,可以拥有更好的性能。

规则质量评价函数φ(r)的定义[9]为式中的r为关联规则,minSupp、minConf、minCF分别是最小支持度、最小置信度、最小确定性因子。由(2)式可以看出,φ(r)的值越大,表明规则的质量越好。在此基础上建立对规则质量评价的指标:
1)ϕ5=maxr1,r2,...,r5φ(r),质量最高的5条规则的平均质量;
2)ϕ10=maxr1,r2,...,r10φ(r),质量最高的10条规则的平均质量;
3)ϕn2=maxr1,r2,...,rn2φ(r),质量最高的n2条规则的平均质量,n为挖掘出的规则总数。
2.3 改进Apriori算法的挖掘步骤
根据2.1提出的新的支持度计算方法和2.2引入的确定性因子,结合传统Apriori算法的挖掘步骤,最终改进关联规则算法的计算步骤如下:
1)设定minSupp、minConf和minCF的阈值与隶属度函数;
2)对数据库进行扫描,得到不包含连续数据的候选1-项集,然后在候选1-项集内的每个项后面加上表示连续数据的Y,使得候选1-项集变为T=((Zi,Y1),(Zi,Y2),…,(Zi,YN)),然后按照2.1提出的支持度计算方法计算T项集内各个数据项的支持度,然后与minSupp比较,选取大于minSupp的项,组成频繁1-项集;
3)将频繁1-项集中的任意两个项集彼此连接得到候选2-项集,对候选2-项集进行支持度的计算,然后与minSupp进行比较,选取大于minSupp的项组成频繁2-项集;
4)以此类推,将频繁(k-1)-项集中的任意两个项集彼此连接,得到候选k-项集,然后对候选k-项集进行支持度的计算,再将其与minSupp进行比较,选取大于minSupp的项,组成频繁k-项集。重复该步骤,直到候选N-项集的所有项的支持度都小于minSupp为止,此时频繁(N-1)项集就被称为最大频繁项集;
5)获取最大频繁项集的非空子集,计算各个非空子集之间的置信度和确定性因子,选出同时大于minConf和minCF的规则,这些规则就是强关联规则。
算法流程图见图1。

图1改进Apriori算法流程图Fig.1 Improved Apriori algorithm flow chart
3 改进Apriori算法在乳腺癌患者就诊数据中的应用
3.1 数据的来源与参数的选取
本文的原始数据来自于San Francisco-Oakl and SMSA、Connecticut、Metropolitan Detroit等18个参与SEER项目的注册中心。原始数据包含有4 409 310位癌症患者的就诊记录。本文使用的数据是从原始数据中抽取出的患有乳腺癌后癌症发生扩散的患者数据,扩散方向为结直肠癌、胃癌、女性生殖系统癌症、淋巴癌、呼吸道系统癌症、泌尿系统癌症和其他。
目前的研究发现,乳腺癌中绝大多数为浸润性导管癌,而雌激素受体(estrogen receptor,ER)、孕激素受体(progesterone receptor,PR)和人表皮生长因子受体-2(HER2)是乳腺癌组织中重要的生物学标志物,因此ER、PR和它们相对应的预后指标(ERA、PRA)也成为乳腺癌重要的预测因子[10]。在乳腺癌发生、发展的过程中,细胞形态学变化的规律是“正常乳腺上皮细胞→乳腺一般增生→乳腺不典型性增生→乳腺癌”,其发生、发展、扩散都与肿瘤的组织学分级等密切相关[11]。原始数 据包含的 参数中,表示ER和PR的是erstatus和prstatus,表示ER和PR对应 的 乳腺癌预后指标的参数是TUMOR_1V和TUMOR_2V,表示肿瘤组织学分级的参数是T_VAL⁃UE、N_VALUE和M_VALUE(这3个参数都是根据AJCC第八版文献来划分[12])。由于年龄和雌孕激素受体有关联[13],且本文探究的是乳腺癌扩散的预测,所以代表年龄的参数AGE_DX和代表乳腺癌扩散方向的参数DIRECTION也需要在实验的时候被考虑。最终本文选取10个参数 进 行 实 验,它 们 分 别 是erstatus、prstatus、her2、TUMOR_1V、TUMOR_2V、T_VALUE、N_VALUE、M_VALUE、AGE_DX、DIRECTION。
3.2 连续型数据的模糊化
由于3.1选取的10个指标中的年龄是连续型数据,所以需要进行模糊化,使其能够被关联规则算法处理。模糊化的第一步是划分模糊区域。数据中的年龄的值域为[14,107],所以此次讨论的论域为[14,107]。利用模糊聚类方法对数据进行模糊聚类划分,将年龄数据分为青年、中年、老年3个模糊区域。第二步是确定隶属度函数。实践中,隶属度函数存在很多不同类型,例如三角波形、梯形波形、高斯波形、钟形波形、S型波形和S曲线波形[14],本文参考Zadeh[15]对年龄属性的划分,选用梯形波形。结合本文使用的实际数据进行调整,最终得到的隶属度函数为

3.3 改进算法对比分析
利用隶属度函数将年龄数据模糊化之后,使用改进算法进行挖掘,并且将结果同使用传统Apriori算法挖掘的结果进行对比,其中使用Apriori挖掘时为了解决Apriori算法无法处理连续型数据的问题,通过对连续型数据直接划分来达到离散化的目的,为了保证论文的严谨性,沿用连续数据模糊化时的划分标准,将年龄直接划分成{[14,44),[44,69),[69,107]},这3段分别对应青年、中年、老年。设定最小置信度为0.8,最小确定性因子为0.7,通过比较最小支持度不同时这两种方法的规则数量和规则质量,对这两种方法进行评判。图2和图3表明,改进后的算法得到的规则数是持续大于改进前的算法的,也就是说改进后的算法可以得到更多的规则。
由图3可以看出,若是只考虑包含有DIRECTION属性的规则,在minSupp较低的时候改进后的算法挖掘出的规则数量相对原算法有显著的增加,但是随着minSupp的增加,改进算法的效果将会逐渐降低,这是因为当minSupp足够大时,规则数量已经大大减少,规则基本已经具有高质量,所以调整就变得困难和不必要。例如,在图3中,minSupp为0.062 5时,改进后的算法多得到了114条规则,但是,当minSupp上升到0.087 5时,改进算法只多得到了17条规则。
再使用规则质量评价指标φ5、φ10、φn2这3个度量来进一步验证改进算法。表1中收集的是在最小置信度为0.8,最小确定性因子为0.7,最小支持度不同的情况下,分别使用两种算法挖掘出的包含有DIRECTION属性的规则的φ5、φ10、φn2这3个度量的值。从表1中可以看出,在最小支持度小于0.1时,改进后的算法得出的3个度量的值总是超过改进前算法的。
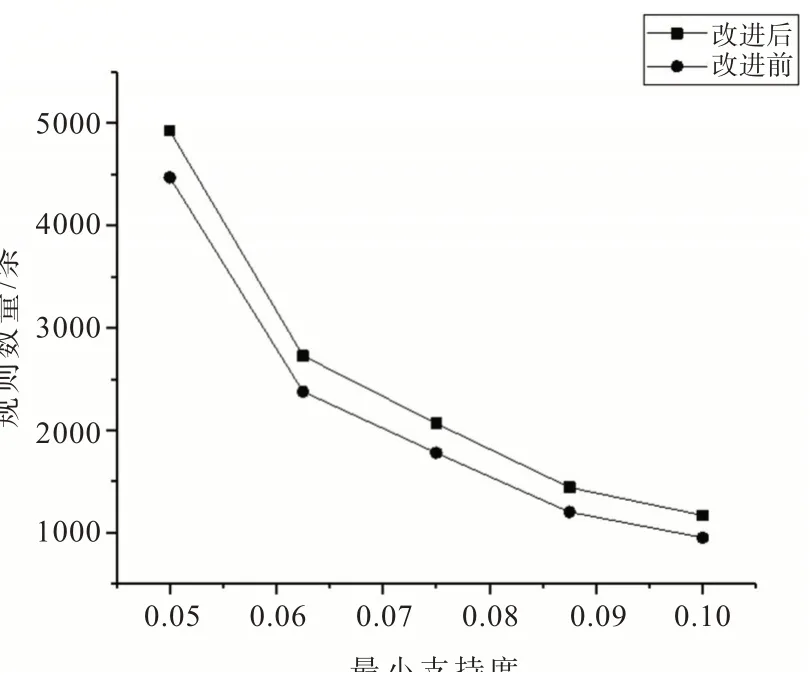
图2不含扩散方向的规则数量Fig.2 Number of rules without diffusion direction

图3包含有扩散方向的规则数量Fig.3 Number of rules with diffusion direction
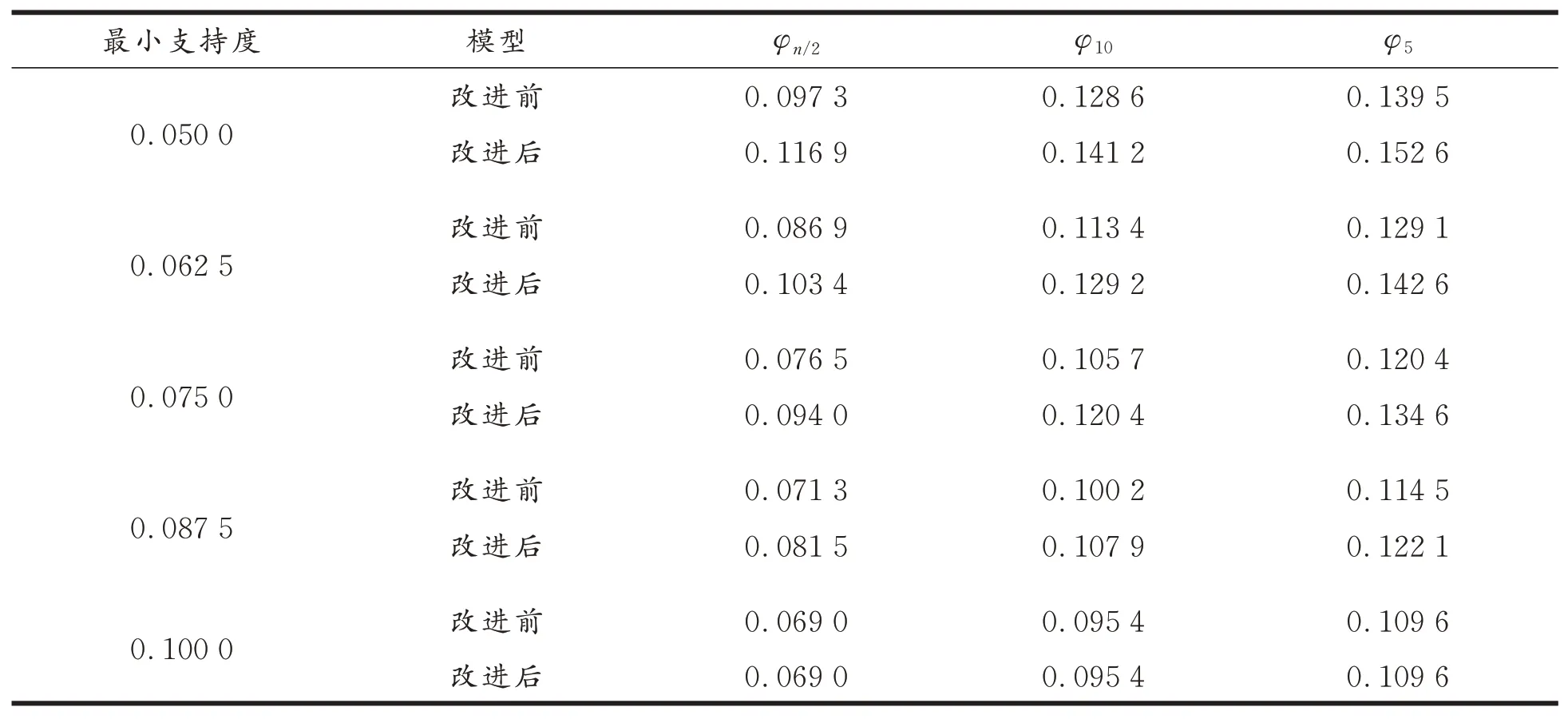
表1规则质量Tab.1 Rule quality
3.4 实验结果
从图2和图3可以看出,最小支持度小于0.075时,改进算法挖掘出的规则数量过多,规则中含有大量冗余规则,而最小支持度大于0.075时,规则数量过少,很多有价值的规则被删除,会影响最终结论,所以取最小支持度设为0.075时挖掘出的规则进行研究最合适。部分挖掘出的规则如表2所示。根据挖掘出的关联结果,得到以下结论。
1)由规则1可以看出,PR和PRA都为阴性的患者在样本中的比例为7.72%,全部扩散成结直肠癌。
2)由规则2可以看出,T_VALUE的值为T1且处于老年(69岁以上)的患者在样本中的比例为9.28%,其中80.02%的患者扩散成结直肠癌。
3)由规则3可以看出,ER、PRA和ERA的值都为阴性的患者在样本中的比例为7.51%,其中84.29%的患者扩散成女性生殖系统癌。
4)由规则4可以看出,ER、PR为阴性且处于老年的患者在样本中的比例为7.76%,其中82.08%的患者扩散成结直肠癌。
5)由规则5可以看出,ER、PR为阴性,ERA为阳性且T_VALUE的值为T1的患者在样本中的比例为9.86%,其中95.76%的患者扩散成呼吸道系统癌。
6)由规则4、5可以看出,若患者ER和PR都为阴性,乳腺癌有较大概率发生扩散。医院给患者制定治疗方案时,可以根据这两项指标的检测值对治疗方案进行调整。
7)由规则2、4可以看出,若患者处于老年,则乳腺癌有较大概率发生扩散,医院在对老年乳腺癌患者进行治疗时需注意。

表2关联规则结果Tab.2 Results of association rules
4 结语
本文主要研究了改进关联规则算法在乳腺癌扩散预测中的应用,引入模糊集理论对Apriori算法进行改进,使用Apriori和改进算法对乳腺癌患者就诊记录进行实验处理,并比较了算法的性能。通过对乳腺癌患者就诊数据进行挖掘,得到乳腺癌扩散和各个参数之间的内在联系,挖掘出有效的规则,为乳腺癌患者的临床治疗提供帮助。
