一种改进的个体激活因子比例仿射投影算法

杨海斌

（湖南理工职业技术学院，湘潭 411004）

0 引言

当一个系统的脉冲响应系数中有一小部分具有显著值，而其他系统的系数接近于零时，则该系统被归类为稀疏系统。对于这样的系统来说，系统辨识算法是一个具有挑战性的任务。仿射投影算法在识别稀疏系统时性能较差。在文献[1]中引入的比例仿射投影算法，通过采用与相应的系数大小成比例的步长调节矩阵来解决这个问题。这种算法尽管在初始阶段有很好的收敛速度，但在整个自适应过程期间无法保持这种速度。文献[2]中引入的改进PAPA算法（MPAPA），使用非线性关系来调整其系数，使所有的系数收敛于最优值的一个界。但MPAPA中激活因子对所有系数都是共有的，并且依赖于自适应滤波器系数向量的瞬时无穷范数，这种计算激活因子的方法导致自适应滤波器系数之间的增益分布不完全符合比例化的概念，其在更新非活动系数时收敛速度会受到影响。为解决此问题，文献[3]利用个体激活因子替代全局激活因子，提出了IAF-MPAPA算法，其比MPAPA算法提供了更好的增益分配。在IAF-MPAPA算法中，需要对格拉姆矩阵求逆，为了避免计算困难，常用一个称为正则化因子来对矩阵进行正则化，文献[4]指出更大的正则化因子导致更小的稳态状态，但收敛速度较慢。具有固定正则化因子的IAF-MPAPA需要在快速收敛速度和低稳态失调之间进行权衡。针对此问题，文献[5]通过对IAF-MPAPA的稳态分析，将正则化因子与稳态分析的关系用数学形式表示出来，然后，在进化方法的推动下，提出了具有进化正则化的IAF-MPAPA算法（ERIAF-MPAPA）。但由于ERIAF-MPAPA算法在整个自适应过程中将非活动系数的增益转换为活动系数的增益，降低了稳态过程中不活跃系数的收敛速度。为此本文提出了一种改进的ERIAF-MPAPA算法（MERIAF-MPAPA），其使用一种新的增益分配策略来更新滤波器系数。该策略在活跃系数接近收敛时增加分配给非活跃系数的增益，且每当学习过程中跨越一个预定义的阈值时，会执行一个新的增益分配，而不是像ERIAF-MPAPA算法那样将增益与系数大小成正比。新算法使能量在整个学习过程中得到了更好的分配，可以更快的收敛。

1 比例自适应算法

图1是回声消除系统的原理框图，图中远端信号x(k)通过回声信道h产生回声yˉ(k)，近端信号d(k)是由回声yˉ(k)混和得到。通过使用FIR自适应滤波器w来模拟回声信道h，可以使所得y(k)逼近回声信号，进而达到回声消除的目的。

图1 回声消除系统

在回声路径识别方面，由于脉冲响应时间长且稀疏，NLMS等传统的自适应算法性能相对较差。PNLMS类型算法通过为每个滤波器数分配步长提高了NLMS算法性能。在PNLMS中，实际回波路径脉冲响应及其估计和滤波器输入矢量定义为h=[h1h2…,hN]Tw(k)=[w1(k),w2(k),…,wN(k)]T，x(k)=[x(k)x(k-1),…,x(k-N+1)]T，其中N是自适应滤波器的长度，k是时间指标。并定义d(k)、e(k)表示所需的响应和误差信号。即：

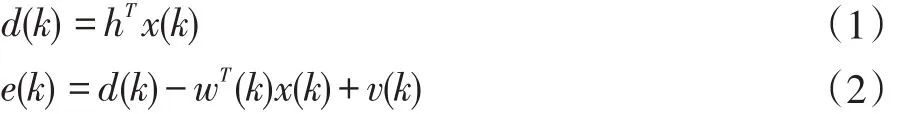
其中v(k)表示近端噪声信号。PAPA类型算法是PNLMS类型算法的多维推广，其通过采用“数据重用”方法对一段数据中的元素进行多次利用改进了PNLMS算法的收敛性能。其输入X（k）为由P个输入信号向量组成的矩阵[6]：

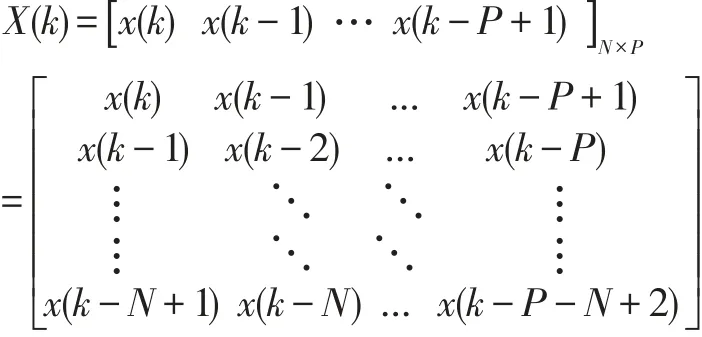
P为数据重用因子（又可称之为投影阶数）。并分别记D(k)、E(k)和ε(k)为k时刻的前P个期望输出、先验估计误差和后验估计误差所构成的向量，即：

式（3-4）中：

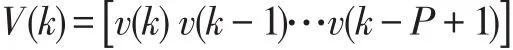
ERIAF-MPAPA算法系数更新过程可表示为：

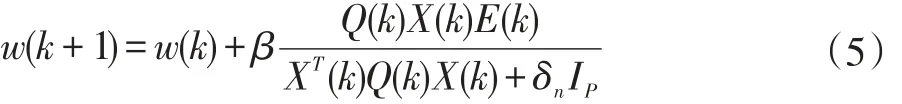
式中β为步长参数，δn是防止被零整除保证稳定的正则化因子，其计算过程如下：令：

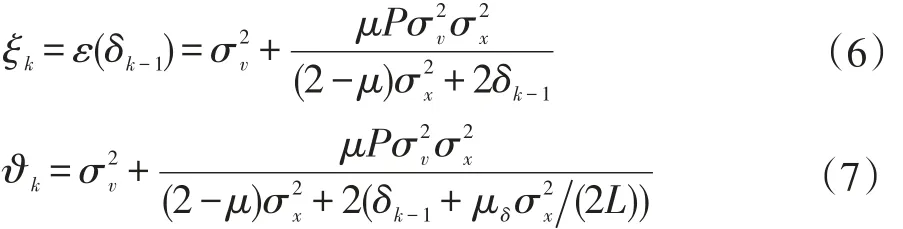
式（5）中Q(k)=diag{q0(k)q1(k)...qL-1(k)}是一个对角矩阵，以更新每个滤波器的估计系数，根据对角元素qi(k)计算式中活化因子fi(k)的区别，PAPA类型算法可分为 IPAPA、MPAPA、IAF-PAPA、ERIAF-MPAPA 等，对于ERIAF-MPAPA，对角元素qi(k)按照如下递归关系式进行计算：

式（11）中fi(k)初始值fi(0)=10-4。

2 MERIAF-MPAPA算法

与IPAPA、MPAPA算法相比，ERIAF-MPAPA算法通过fi(k)将部分非活动系数增益转移到活动系数增益，提供了更好的增益分布使得稳态前的收敛速度和跟踪能力都得到了很大的提高；但它减缓了稳态阶段不活动系数的收敛速度。针对此问题，本文提出一种新的自适应系数增益计算策略。该方法的基本思想是：因对已经达到收敛的自适应系数分配较大的增益实际上对全局收敛没有影响，所以EIAF-MPAPA算法的比例原理不需要在整个自适应过程中应用。在增益分配的新策略中，目标是当第i个系数达到其最优值wi,opt的邻近点ε时，重新设计一个新的策略来分配自适应性增益，目标函数定义为[8]：

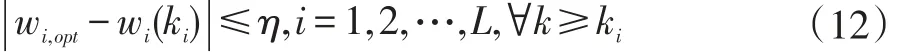
其中wi(ki)是第i个系数的估计值，ki是第i个系数达到最优值所需的迭代次数，η为预定义的阈值。η的范围可由误差信号E2(k)的期望值E(E2(k))来确定，E(E2(k))计算如下：

对于MERIAF-MPAPA算法，考虑系数在k次迭代时达到最优值的邻近点ε，于是有：

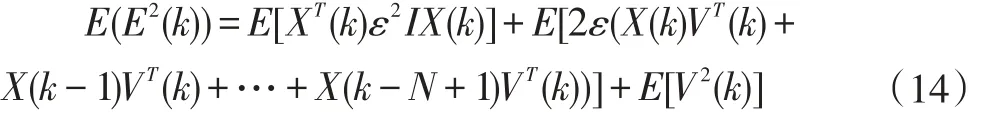
假设X(k)和V(k)是不相关的信号，得到：

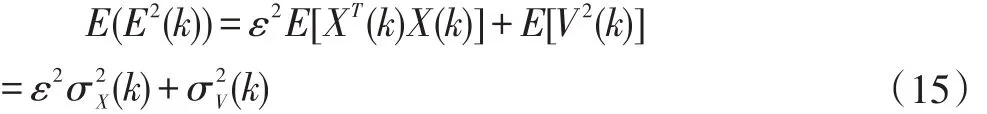
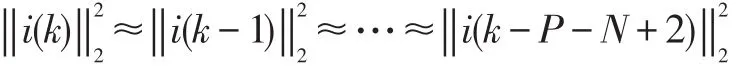
于是，式（15）可写为：

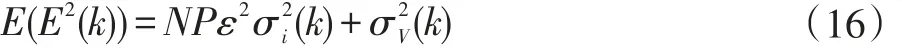
因增益分布的变化必须在达到稳态之前发生，因此η的值必须大于(k)。因此可以用下式来确定η的范围：

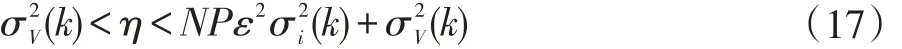
从式（12）可看出，在ki迭代时刻，第i个系数几乎已经收敛，因此，这个系数不再需要获得与其幅度成正比的增益。这样，以前分配给这个系数的部分增益现在可以重新分配给没有达到最优值邻近点的系数，从而加快它们的收敛速度。因此，考虑到阈值条件（12），每个系数的单个增益被重写为：

上式中，对已收敛到最优值的系数，则分配最小增益γi(k)。在式（18）中，我们注意到这种增益分配策略需要事先知道wi,opt的值。但在实际应用中，系数的最优值不是先验知道的。因此引入如下的瞬时平方误差的平滑函数ψ(k)：

其中0<α<1是平滑因子。因此，在MEIAF-MPAPA算法中，考虑到全局阈值条件，第i个系数的增益表示为：

于是可得增强的MERIAF-MPAPA算法完整递推公式为：

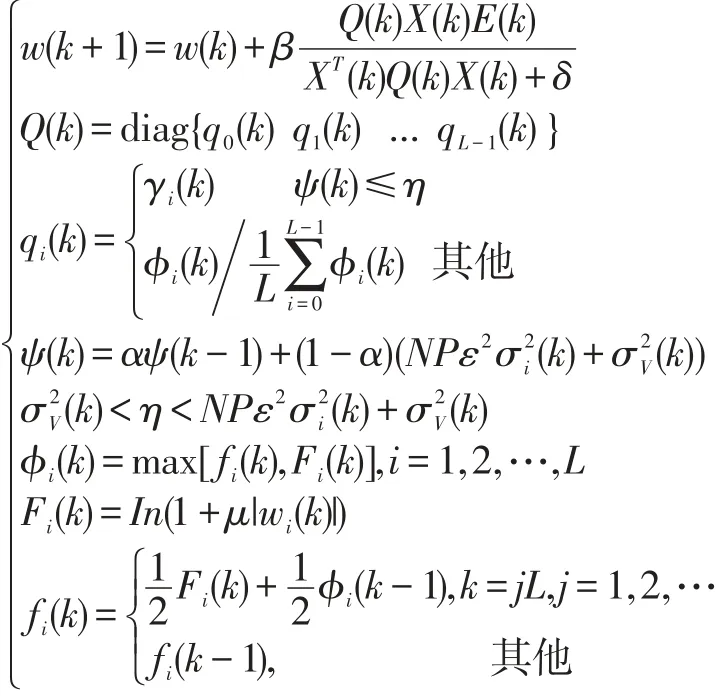
3 仿真分析

为验证本文算法性能，针对一个高度稀疏的回声消除系统，通过蒙特卡罗模拟（平均100次独立运行）比 较 MPAPA、IAF-MPAPA[2014]、ERIAF-MPAPA[2017]和MERIAF-MPAPA算法的性能。四种算法中数据重用因子P=2，为模拟回波路径脉冲响应，首先定义如下以指数方式衰减的Lu维向量：

其中τ>0是衰变常数。利用方程（21），得到脉冲响应为：

在所有的模拟实验中，输入信号是一个相关的、方差为=1的2阶零均值自回归过程，即：

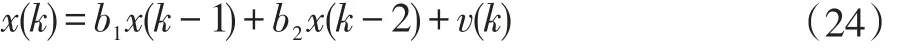
其中b1和b2是过程系数。并采用归一化失调（misalignment）作为性能比较标准，其定义为：

从图2可以看出，在所有算法中，本文提出的算法收敛最快。

图2 算法收敛性能比较

4 结语

本文提出了一种改进的ERIAF-MPAPA算法（MERIAF-MPAPA），该算法在学习过程中使用了一种增益再分配策略，以增加分配给非活动系数的增益，因为活动系数趋于收敛。其次，当达到阈值时，通过对所有自适应系数分配相等的增益来实现这种再分配。仿真结果表明，该算法的收敛速度明显提高。