基于增量矩阵分解的协同过滤推荐模型研究
2020-08-10樊艳清李明智纪佳琪
樊艳清,李明智,纪佳琪
(1.河北民族师范学院信息中心,承德 067000;2.河北民族师范学院数学与计算机科学学院,承德 067000)
0 引言
大数据时代,推荐系统可以帮助用户从海量信息中选择自身感兴趣的物品。在众多推荐模型中,协同过滤以其简单性及有效性得到了广泛的应用[1]。协同过滤模型通过对代表用户喜好程度的“用户-物品”评分矩阵进行建模,然后计算填充该矩阵中的缺失数据,最后对这些数据进行排行并取出前N条作为推荐结果。在建模中使用的“用户-评分”矩阵可以分为2类:显示数据和隐式数据。推荐系统的任务也可以分为2类[2]:评分预测和Top-N推荐。在评分预测任务中,一般使用显示数据,对用户评分矩阵中的未知数据进行评分的预测,因此该任务可以转换为回归任务。然而收集用户的评分数据是十分困难的并且是稀疏的,因此很多场景会使用隐式数据。相对于显示数据隐式数据更好获取,如用户的点击、收藏、购买等都可以看成隐式数据。在这种情况下,“用户-物品”评分矩阵中存储的并不是用户对物品的评分,而是1或0值,分别表示用户对物品有行为和无行为,此时推荐任务可以转换成一个二分类任务。
本文主要使用隐式数据解决Top-N推荐问题。在之前的研究中,一般都是获取到全部训练数据,然后设计推荐模型[3]。这样的模型对于用户兴趣改变不大或物品变化不大的场景下比较适用,然而对于一些场景并不适用:如音乐或电影,用户会随着时间迁移,其喜好的类型会变化;再如新闻,其更新速度较快,用户关注点变化也会较快。因此本文不再使用固定数据训练模型,而是把数据看成数据流,是随着时间的流逝不断进入到模型中的,模型要能实时处理这些进入的数据并对其进行训练,同时实时地更新模型。这类模型称为增量模型,在数据进入时使用矩阵分解方法,因此本文提出的模型称为增量矩阵分解的协同过滤推荐模型。
1 相关工作
在推荐系统初期,由于Netflix[4]竞赛的盛行,研究者提出了众多基于矩阵分解的推荐算法,这类算法无论在推荐性能上还是时间复杂度上都优于其他类型的推荐算法。矩阵分解思想最初来源于信息检索领域的隐语义索引(Latent Semantic Indexing,LSI)[5]方法,LSI使用了奇异值分解(Singular Value Decomposition,SVD)[6]算法对“文档-词”矩阵进行分解。在推荐系统领域,矩阵分解(Matrix Factorization,MF)[7]算法借鉴了上述思想,通过对“用户-物品”评分矩阵进行分解,使得可以用一个隐空间来表示用户和物品。假设用R表示评分矩阵,P和Q表示分解后的隐空间,即P表示用户隐空间,Q表示物品隐空间。Pu表示P矩阵中的一行即用户隐向量,Qi表示Q矩阵中的一列即物品隐向量,表示对矩阵R中u行和i列即用户u对物品i的预测评分。此时推荐问题可以转化为公式的优化问题。
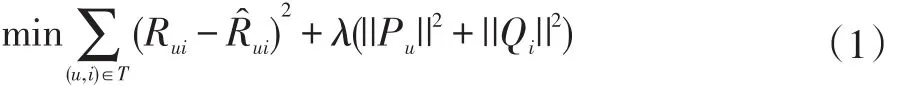
其中T表示训练数据,即用户对物品的评分数据,λ是正则化参数,||Pu||2+||Qi||2是正则化项用来避免过拟合问题。接下来可以使用梯度下降法(Stochastic Gradient Descent,SGD)对该模型进行优化。对于给定的训练元组
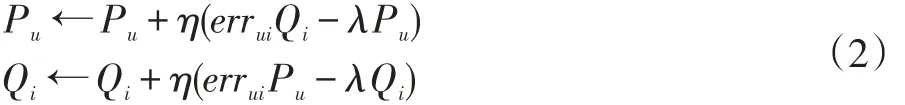
对于矩阵分解模型的算法描述如算法1所示。
算法1:矩阵分解模型算法
输入:T=
输出:P,Q
1. for u Users(T):
2.Pu←Vector∈Rk
3. 取值范围为(0,1)
4. for i∈Items(T):
5.Qi←Vector∈Rk
6. 取值范围为(0,1)
7. for count in 1 to iters:
8. for
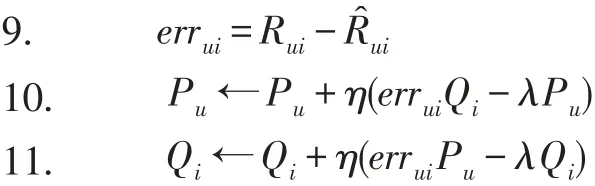
上述算法是矩阵模型的基本算法,其中T为输入的训练数据,k为隐空间的维度,iters为算法的迭代次数,λ为正则化参数,η为学习率。
2 基于增量矩阵分解的协同过滤推荐模型
在上一节描述的矩阵分解模型中,训练数据是固定,当有新增数据时必须从新启动模型的训练,无法适应流式数据,即无法完成在线训练和实时更新。为了解决这个问题,本文提出了一种增量矩阵分解的协同过滤算法,该模型可以适应流式数据。即当有新数据到来时,不必从新训练整个模型,而是基于当前数据在已有模型基础上训练并实时更新模型。其算法如算法2所示。
算法2:基于增量矩阵分解的协同过滤
输入:流式数据 T=
输出:P,Q
1.for
2.if u∉Rows(P):
3.Pu←Vector∈Rk
4.Pu取值范围为(0,1)
5.if i∉Rows(QT):
6.Qi←Vector∈Rk
7.Qi取值范围为(0,1)
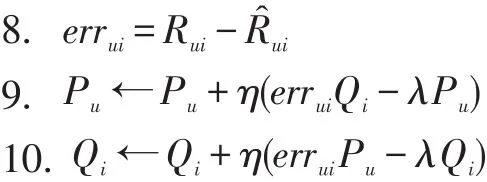
从算法2可见,该模型是一种增量更新方式,当有新的观测数据到来时就对P和Q进行实时更新。尽管形式上与矩阵分解模型相似,但是其区别也很明显。首先,当有新数据到来时只对当前数据迭代一次,然后就更新参数P和Q。当然当有新数据到来时对当前数据迭代n次也是可以的,这样可以获得相对更好的精度,但是考虑到迭代次数越多消耗的时间越长,而本模型要适应实时在线更新,因此权衡时间和精度等因素后本文还是采用迭代一次的方案,舍弃一点精度的损失来换取时间上的减少。其次,该模型可以是已经经过预训练的,即利用之前已有的训练数据做一次全量训练(利用算法1),然后再做增量训练(利用算法2)。
算法2中使用的数据为隐式数据,即评分矩阵中的数据要么为1表示正例,要么为0表示负例。此时为0的负例可能有2层含义:用户不喜欢该物品和用户对该物品还未有过行为。本文假设为0的负例都是用户对该物品还未有过行为。这种假设的原因是:可以抽取部分负例参与训练而不是全部参与训练。由于数据中只含有0和1,因此误差的计算可以使用表示。
当迭代完成后,R矩阵中的所有位未知项都已计算完成,此时分别对每个用户对物品的预测评分值进行降序排序,然后取出前N个物品作为该用户的推荐物品。
3 实验
推荐系统常用的评价方法是,把数据集随机的分成训练集和测试集,用训练集对模型进行训练,用测试集对模型进行评价[8]。然而本文提出的算法并不能使用上述评价方法。主要原因如下:
●数据的顺序:由于本文提出的模型要适应流式数据,即数据的到来是有先后顺序的,这种顺序不能打乱。因此在拆分训练集和测试集时,要保证其按时间的顺序性。
●实时性:本文提出的模型是一种增量更新的模型,当有新的数据到来时,会立即使用这个新数据对已有模型进行再训练然后更新模型。
因此,本文使用一种能够适应流式数据的评价推荐系统的方法。首先,我们先使用部分数据对模型进行一个预训练,形成一个基本可用的模型。然后按照数据生成的时间顺序,分别把数据
(1)如果user是一个已知用户(即已经在初始训练数据集中出现过的用户),则使用当前模型推荐N个物品给用户user,否则进入第3步。
(2)对当前的推荐进行评价的计算。
(3)用当前数据重新训练模型并进行模型更新。
(4)等待下一个(批)数据的到来,然后转向1。
3.1 数据集
本文使用3个数据集进行模型的评价,其详细描述见表1。所有的数据集都会处理成按时间顺序排列的
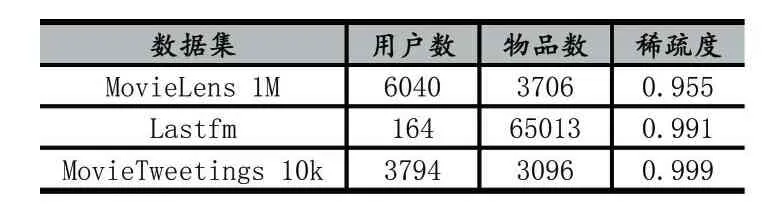
表1 数据集详情
3.2 结果分析
本文与 ItemKNN(Item-based Collaborative Filtering)[9-10]和 BPRMF(Bayesian Personlized Ranking Matrix Factorization)[11]2个基线算法进行了对比。ItemKNN是推荐系统中较早的模型,目前已广泛用于工业实践,因此与之对比有一定的实践意义。BPRMF是使用矩阵分解方法并取得较好效果的推荐模型,本文也是在其基础上进行了增量更新的改进。
本文使用召回率(Recall)和模型更新时间(Update Time)作为评价指标。其中Recall@N表示推荐N个物品时的召回率。实验结果见表2。
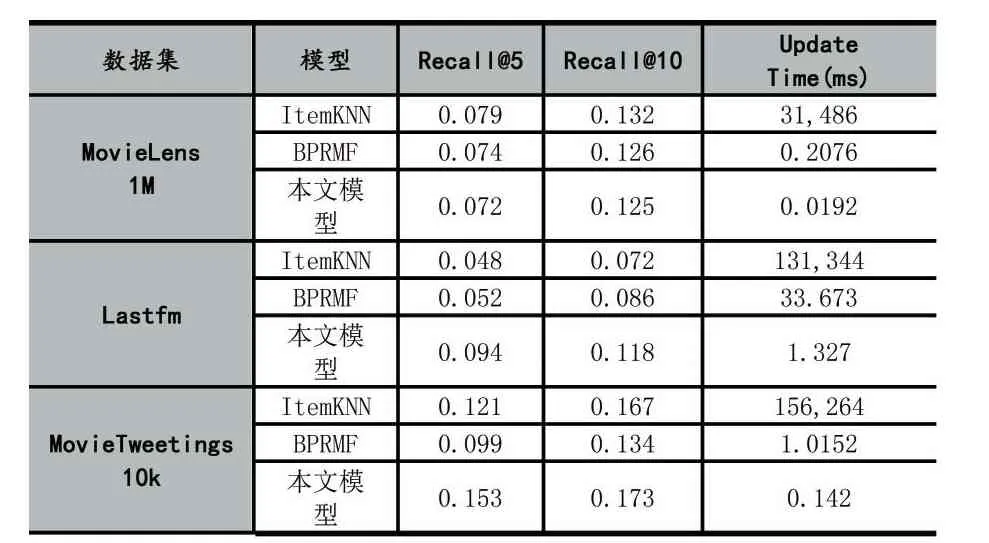
表2 实验结果
从实验结果可以看出,本文提出的模型在更新时间上明显快于其他2个模型,在三个数据集上比排在第二的模型分别快10.8倍、25.4倍和7.1倍。召回率上,本文模型在Lastfm和MovieTweetings 10k数据集上明显高于另外两个模型。虽然在MovieLens 1M数据集上Recall低于其他两个模型,但是差异并非很大,与之相对,在更新时间上分别快于其他两个模型1639倍和10.8倍。因此综合看来,本文提出的模型在增量更新的性能上明显优于其他2个模型。
4 结语
目前众多的推荐模型都是离线完成模型训练然后上线使用,在积累了一定的新数据后在离线从新进行训练,为了能够实时更新推荐模型以适应在线更新,本文提出了一种基于增量矩阵分解的协同过滤模型用于完成Top-N推荐任务。当每次有新数据到来时就进行模型的训练和更新,使得模型能够实时应用。在下一步的工作中,我们将比较更多的数据集和更多的基线算法,同时进一步优化已有模型。
