“体验式”数学教学联通“体验”与“经验”

张亚杰?任莉

为了更好地优化教学方式，提高课堂教学质量，北京市海淀区双榆树第一小学（以下简称“双榆树一小”）“育·树”生态课堂聚焦学生六个关键能力培养—独立思考、合作探究、信息筛选、分享交流、迁移运用、质疑反思，以满足学生个性化学习需求和立德树人总体目标达成。数学团队以“立足学生的未来发展”为核心，尝试“体验式”数学教学。

一、“体验式”数学教学的一般过程：一个核心，两个维度，三个意识，四个重点

（1）一个核心：以学生的未来发展为核心。

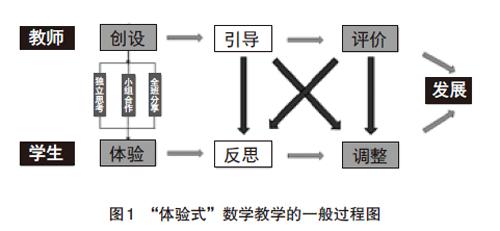
（2）两个维度：教师维度是“创设—引导—评价”教学方式，学生维度是“体验—反思—调整”学习方式。

（3）三个意识：服务意识—教师的教是为学生的学服务的，“创设”是为“体验”服务的，“引导”是为“反思”服务的，“评价”是为“调整”服务的;经历过程意识—经历体验情境的过程，经历评价反思的过程，经历调整建构的过程;发展意识—学生的知识、能力得到发展，学生的思维、方法得到发展，学生的情感、价值观得到发展。

（4）四个重点：第一，教师为学生创设情境，必要时给予学生引导，适当给予学生评价反馈;第二，学生在情境中感受体验，进而思考、反思，触发自主调整与建构;第三，“创设为体验服务”的环节具体包括三种方式，即独立思考、小组合作和班级分享，帮助学生在课堂中更好地体验;第四，教与学不是孤立存在的，而是会互相影响、促进，最终通过双边互动帮助学生获得思维的发展。引导会促进调整的发生，评价会促进反思的深入。（见图1）

二、“体验式”数学教学“四环节”：创设情境、自主探究、合作交流、深化拓展

学生在一定的情境下，参与数学活动，经历数学知识的形成和应用过程，积累数学活动经验，从而获取知识、应用知识、解决问题，达到自主发展的目的。

（1）创设情境，激发体验：课堂教学中，教师应创设自主探究学习的情境，激发学生探究的欲望。比如，凸显问题情境，找到新旧知识的结合点，确定学生的“最近发展高度”，设置问题情境。

（2）自主探究，尝试体验：教师要给学生足够的时间和空间，让学生自己决定探究的方向，用生活经验和思维方式开放地探究体验数学知识的产生和发展过程。

（3）合作交流，丰富体验：师生、生生之间的合作互动，可以给予学生更大的自由活动空间和更多的相互交流机会。教师要鼓励学生积极地进行数学交流，分享彼此的经验，使学生在合作、讨论、探究中，与他人的体验产生碰撞，在碰撞中促进发展，从而在数学交流中获得更丰富的体验。

（4）深化拓展，迁移体验：将学到的知识应用到具体问题中去，才能促进知识的内化，知识才能活化。深化拓展情境，才能促进学生学习的正向迁移，使学生的认知进一步结构化。因此，教师应以学生为出发点，挖掘问题的多向性和分类设计的拓展性，让每个学生都有迁移体验，激励求异思维。

三、搭建“体验”与“经验”之间桥梁联通的课堂教学结构：三轴四链一循环

结合“体验式”数学教学的一般过程，双榆树一小校长丁凤良带领数学团队研究、实践并探索出有助于帮助学生搭建“体验”与“经验”之间的桥梁的数学课堂教学结构，简称“三轴四链一循环”（见图2）。

（1）“三轴”：包括教学方法、教学策略和教学成果三个部分。教学方法即暴露—碰撞—提升—运用;教学策略即独立—合作—引导—迁移;教学成果即原有经验—生成经验—再生经验—稳定经验。

（2）“四链”：主要包括独立完成暴露原有经验、合作探究碰撞生成经验、引导提升再生经验、迁移运用稳定经验。

（3）“一循环”：主要指的是学生活动经验的积累是在循环迭代、主动建构的过程中进行的。学生活动经验的积累必须在经历、体验的基础上，通过理解、内化的过程，最后重组、优化，主动建构形成比较稳定的数学活动经验。“三轴”依次递进，相互作用;“四链”互为基础，彼此联系;“一循环”往复更替，不断积淀。

“三轴四链一循环”的教学结构强调三点。第一，前一次数学活动的经验是后一次数学活动的基础，后一次数学活动的经验是前一次数学活动经验的巩固和发展。第二，教师要注重让学生亲身经历观察、描述、操作、猜想、实验、思考、推理、分析、交流、应用的数学活动过程，要在“过程”中唤醒经验、累积经验、反思经验、提升经验，运用甚至重新创造经验。第三，最终的目标就是要让学生模糊的经验变得清晰起来，让片面的经验变得完善起来，让错误的经验变得正确起来，让零散的经验变得结构化起来。以北师大版三年级上册“长方形的面积”为例。

活动：探究2019年园艺博览会发行的邮票面积。

【链条一】学生独立思考，暴露、激活原有的度量图形面积的经验

教师提出独立思考的要求：为了纪念最近举办的世界园艺博览会，中国邮政发行了纪念邮票（见图3）。你们知道这张邮票有多大吗？怎样解决这个问题？

此环节让学生独立思考，用自己的方法得到邮票的面积。这样的設计给予学生足够的活动空间，学生在经历如何求得邮票的面积的过程中，可以用不同的方法。学生原有度量面积的经验被暴露，思维从直观形象层面上升到空间想象的阶段。

【链条二】学生小组合作，交流、碰撞生成计算长方形面积方法的经验

小组活动建议：①以4人小组为单位在组内交流方法;②小组成员轮流发言，说清自己的方法;③共同商量确定一种方法，向全班分享。教师巡视，发现并回应、解答学生在合作过程中遇到的问题。

预设生成1：用小正方形纸全部铺满邮票，最后数一数一共用了多少个小正方形纸，根据1张小正方形纸的面积是1平方厘米，就可以算出邮票的面积是12平方厘米（见图4）。

预设生成2：用小正方形纸分别铺满邮票的一个长边和一个宽边，长边铺了4张，宽边铺了3张，由乘法可以得到，一共铺了12张小正方形纸，就可以算出邮票的面积是12平方厘米（见图5）。

预设生成3：小正方形纸不铺满邮票，依据对应关系，最后算出一共用了多少张小正方形纸，就可以算出邮票的面积是12平方厘米（见图6）。

预设生成4：小正方形纸不铺满邮票，依据对应关系，最后算出一共用了多少张小正方形纸，就可以算出邮票的面积是12平方厘米（见图7）。

预设生成5：学生用刻度尺量出邮票的长是4厘米，宽是3厘米，而邮票是长方形，又知道长方形的面积=长×宽，所以邮票面积是4×3=12（平方厘米）。

学生在交流碰撞的过程中，在辨析其他同学所提出方法的过程中，进一步明确了不同方法之间的联系，为理解长方形面积的计算方法奠定了基础。

【链条三】教师引导梳理、归纳、积累面积计算的经验

师生做出小结：长是多少厘米，即沿长边可以摆几个小正方形，宽是多少厘米，即沿宽边能摆几行，因此“长×宽”等于“每行摆的面积单位的个数×行数”，等于“长方形包含的面积单位的个数”，等于“长方形的面积”。所以四种方法结合起来，能进一步解释“长方形的面積=长×宽”背后的道理。

【链条四】拓展应用，迁移运用稳定的经验，积累解决问题的经验

在园博园中还有一片面积为20平方米的长方形月季花圃，请你算一算这个花圃的长和宽各是多少米。

①由长方形的面积=长×宽，想（  ）×（  ）=20，可能长是10米，宽是2米;②接着想可能长是20米，宽是1米;③可能长是40米，宽是0.5米;④可能长是80米，宽是0.5米的一半。

学生通过猜想，既巩固了对长方形面积公式的记忆，又突破了以“整数个”面积单位计量的常规思维。学生在自主解题中，迁移、运用稳定经验，获得了对长方形面积公式更为深入的理解。

学生在经历了独立思考邮票的面积、合作交流分享邮票面积的计算方法、教师引导对比方法之间的联系和区别、运用新生经验自主解题四个过程后，实现了一个认知系列的往复循环：唤醒经验、累积经验、反思经验、提升经验，运用并重新创造经验，真正实现了“体验”与“经验”之间的联通。

（作者单位：北京市海淀区双榆树第一小学）

责任编辑：孙昕

heartedu_sx@163.com