培养学生观察、探索、小结的能力

王永立

(甘肃省华亭市皇甫学校 甘肃华亭 744100)

一、案例背景

笔者担任七年级两个班的数学教学，在给学生辅导数学《练习册》的时候遇到这样一道题：在平面上有n条直线，两两相交，无三线共点；这n条直线把平面最多可分成多少部分？要求学生具有以下认识：(1)学生在掌握一定知识的基础上，具有1+2+3+…+100的计算技巧，具备探究1+2+3+…+n和的能力。(2)学生要掌握平面内两条直线的位置关系以及初步的几何知识。由于学生之间差距较大，因此，我在辅导中注重培养学生的合作交流意识和观察、探索、归纳的思维品质。

二、案例过程

(一)学生的数学知识和经验

1.在小学数学中，绝大多数同学掌握了1+2+3+…+100的计算技巧。那么，对于1+2+3+…+n=( ) (教师：要求学生在练习本上独立完成，对于有困难的请求同桌帮助；教师在巡视时发现能得出结论的学生人数不多。)

接着，教师点评两位学生的回答都很好。尤其是第二个同学的回答，他给出了连续多个数的求和方法。

(二)问题探究

1.教师趁热打铁，紧随着给出以下问题。例如，在一次运动会上，有n支球队进行单循环比赛，共有几场球赛，请同学进行探究。

(教师提示如下：球队至少两队，依次增加，比赛场次也随之变化，其规律列举如下：

(球队) 2 3 4 5 6 ……n

(场次) 1 3 6 10 ……(an)

同时，教师给出问题：①下行的数字即场次和上行的球队数有何关系？②能发现什么规律？)

此时，大多数学生独立完成有困难。因此，笔者要求分小组进行合作讨论。教师巡视并参与到个别小组的讨论交流中。在最后，全班同学在教师的指导下，分小组汇报探究结果。最好的小组板书展示如下：

场次数于球队数的对应关系如下：

2.2 超声微泡造影剂携RPM对T24细胞周期分布与凋亡的影响 流式细胞仪检测结果表明经RPM和超声微泡造影剂携RPM处理过后的处于G1期的T24细胞数量明显高于对照组(P<0.05)，并且T24细胞出现大量凋亡(表3，图1)。

在最后，由学生独立算出上式的和，学生很快得出结论：

2.同类型练习。教师不失时机地给出问题：在平面上有n个点A，A，A，……A。其中，没有任何三点共线，这n个点共可确定多少条直线？

3.因势利导，探究前面《练习册》中提出的问题。

(教师：板书下列第一行内容，要求学生填写第二行数字。)

直线条数： 1 2 3 4 5 ……n分平面最多部分数：(2) (4) (7) (11) (16) ……an

(对应的项数) a1a2a3a4a5……an

(个别学生口头回答正确，教师给予表扬和鼓励。)

(教师板书)观察第二行各项的关系有：

上列各式左右分别相加可得：

an-a1=2+_3+4+5+……+n

在最后，教师要求：请同学在练习本上独立完成结果，提前完成的同学帮助其余同学，并让个别学生展示结果：

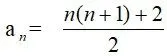
三、案例分析

1.数学教学要密切联系学生的实际，从学生的生活经验和已有知识出发，创设有趣的情境，把数学知识和数学思想方法的学习有机地结合起来。同时，教师要加强培养学生善于观察、联想、类比推理的数学知识的应用能力，只有学生的这些能力提高了，才能达到最终的教学目标。

2.教师要深入研究学生、研究教材，在练习辅导中不能就题论题，要适当地拓展和延伸知识，改进数学知识的呈现方式。这样才能有效地激发学生学习的积极性和自觉性，才有利于培养学生自主探索、归纳推理的数学思维品质。

3.教师要尊重学生的数学思考，重视学生数学方法的掌握及应用。对于每个学生的发现和灵感的闪现，教师要及时地给予肯定和鼓励；对于有些学生的错误，教师不能嘲笑和讽刺，要在纠正的基础上帮助学生分析错误的根源，从根本上解决数学学习中出现的问题。教师可以通过师生互动、生生互动的交流，解决学生学习中存在的疑惑，进而培养学生的合作意识。

4.教师要引领学生回顾与思考解决问题的过程，让学生理解和认识面对一个实际问题时，应该怎样来分析、解决？如何从中提炼出解决问题的方法和策略，并自觉地把数学学习聚焦在数学思想的方法和策略上，从中获得积极的情感体验。