基于时延反馈多稳随机共振的微弱信号检测方法
2020-08-07时培明袁丹真张文跃李梦迪韩东颖
时培明, 袁丹真, 张文跃, 李梦迪, 韩东颖
(1.燕山大学 河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004;2.燕山大学 电气工程学院,河北 秦皇岛 066004;3.燕山大学 车辆与能源学院,河北 秦皇岛 066004)
1 引 言
信号检测技术广泛应用于雷达、勘探、卫星通讯等领域[1,2]。实际检测过程中,被测有用信号往往十分微弱,同时经常淹没在背景噪声下,很难从中检测出有效信号。传统方法主要通过去除和抑制噪声来检测信号,如:小波去噪、自适应滤波法等,但在去除噪声的同时,信号也受到了损失[3,4]。
随机共振是一种利用非线性系统实现噪声能量向信号能量转移的信号降噪检测方法,与传统信号处理中滤除噪声的方法相比,随机共振能保留并利用噪声提高输出信噪比,对噪声背景下微弱信号的增强检测具有独特优势[5]。将随机共振用于微弱信号检测时,噪声信号在一定条件下反而将能量大幅度地向周期信号转移,使得输出信噪比提高,随机共振的特有现象引起很多研究人员的关注[6~9]。Tan J等对变尺度频移随机共振进行了研究,为应用随机共振技术处理大参数信号提供了方法。Li J等对不同稳态的随机共振进行了对比,证明多稳系统模型在增强输出信噪比与提升微弱信号处理能力方面具有更大的优势。
本文提出一种基于一次项时延的多稳态随机共振模型,并推导了该模型的时延福克-普朗克方程,分析了参数对概率密度函数的影响,通过实际微弱信号检测结果验证该模型的可行性和优越性。
2 一次项时延多稳态随机共振模型
一次项时延随机共振是在由周期信号和高斯白噪声诱导的时延反馈随机共振的基础上进行改进的,其势函数U(x)为:
(1)
一次项时延反馈的Langevin方程[10]为:
(2)
时延Fokker-Planck方程为:
(3)
式中:B(x)=D;条件平均漂移项heff(x)为:
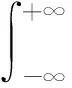
(4)
式中:h(x,xr)=-bxr-cx3-dx5+Acos (2π ft),xx=x(t-τ),p(xx,t-τx,τ)是零阶近似马尔可夫转移概率密度,可以表示为:
(5)
式中:h(x)=-bx-cx3-dx5+Acos(2π ft),将式(5)带入到式(4)中得:
heff(x)=(1+bτ)(-bx-cx3-dx5)
+(1+bτ)Acos (2 π ft)
(6)
在短暂的时延条件下,Langevin方程改为:
(7)
由Langevin方程可知,参数b既是结构参数又是时延反馈强度,对系统调节有很大影响,由式(7)可得一次项时延反馈随机共振的广义势函数为:
(1+bτ)Axcos (2π ft)
(8)
一次项时延随机共振系统的概率密度函数为
(9)
式中N是归一化常数。
3 参数对概率密度函数的影响
概率密度函数表达的是粒子在势阱中停留的概率,有利于进一步分析粒子的运动状态。本节分析了结构参数与时延参数对概率密度函数的影响。图1为2个模型的参数变化对概率密度的影响对比。
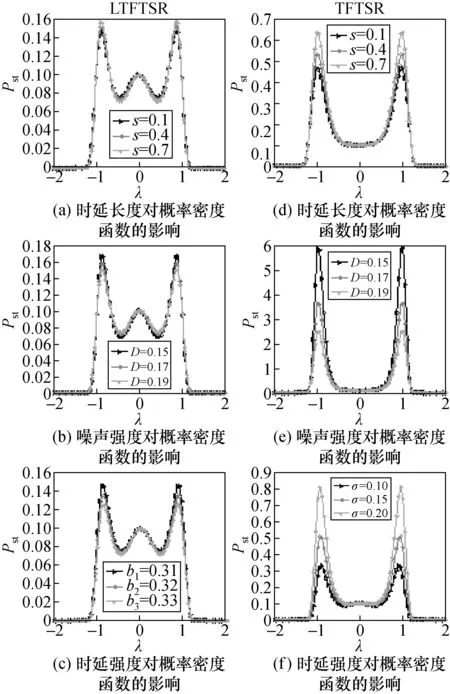
图1 2个模型的参数变化对概率密度的影响对比Fig.1 Comparison of the influence of the parameters of the two models on Pst
如图1(a)显示,时延时间τ越长,2个峰谷越深,两侧的峰值越高。图1(b)中,当其他参数确定时,Pst曲线有3个明显的峰值。随着噪声强度D的增加,两侧的峰值变小,两个峰谷深度变浅。与右侧TFTSR模型相比,时延长度参数τ和噪声参数D对TFTSR模型的影响大于LTFTSR模型。图1(c)中,随着时延强度b的增加,Pst曲线两侧的峰谷和峰值都降低。从图1中的不同参数对LTFTSR的变化曲线可以看出,时延强度b对Pst的影响比噪声强度D和时延长度τ对Pst的影响更大,其中时延长度τ对Pst的影响最小。
4 随机共振系统的度量指标
除了信噪比是评价随机共振结果的指标外,谱功率放大系数也常作为随机共振系统的度量指标,其定义如下:
η=|Xx|2
(10)
式中:Xx为x的线性响应灵敏度。在数值研究中,可以近似为输出信号幅值与输入信号幅值之比,因此可以定义谱功率放大系数为:
(11)
式中:Z(k0)和X(k0)分别是FFT变换后的输入信号和输出信号的单边谱的幅值。若η与噪声强度的曲线图中具有局部最大极值现象,则可判断系统发生了随机共振(stochastic resonance,SR)现象。
为了验证SR现象的发生,根据绝热近似理论的小参数条件,设置输入信号的驱动信号的频率为f0=0.01 Hz,振幅A为0.2 m/s2,采样频率fs=5 Hz。在数值研究中,采用四阶龙格-库塔方法求解SR模型。设多稳态非线性系统的结构参数为c=-0.4,d=0.05。在不同的参数b下,η和SNR随着噪声强度D而变化如图2所示,η和SNR存在一个极大值,这表明SR现象发生,并且随着参数b的增加,SNR的极大值也增大。
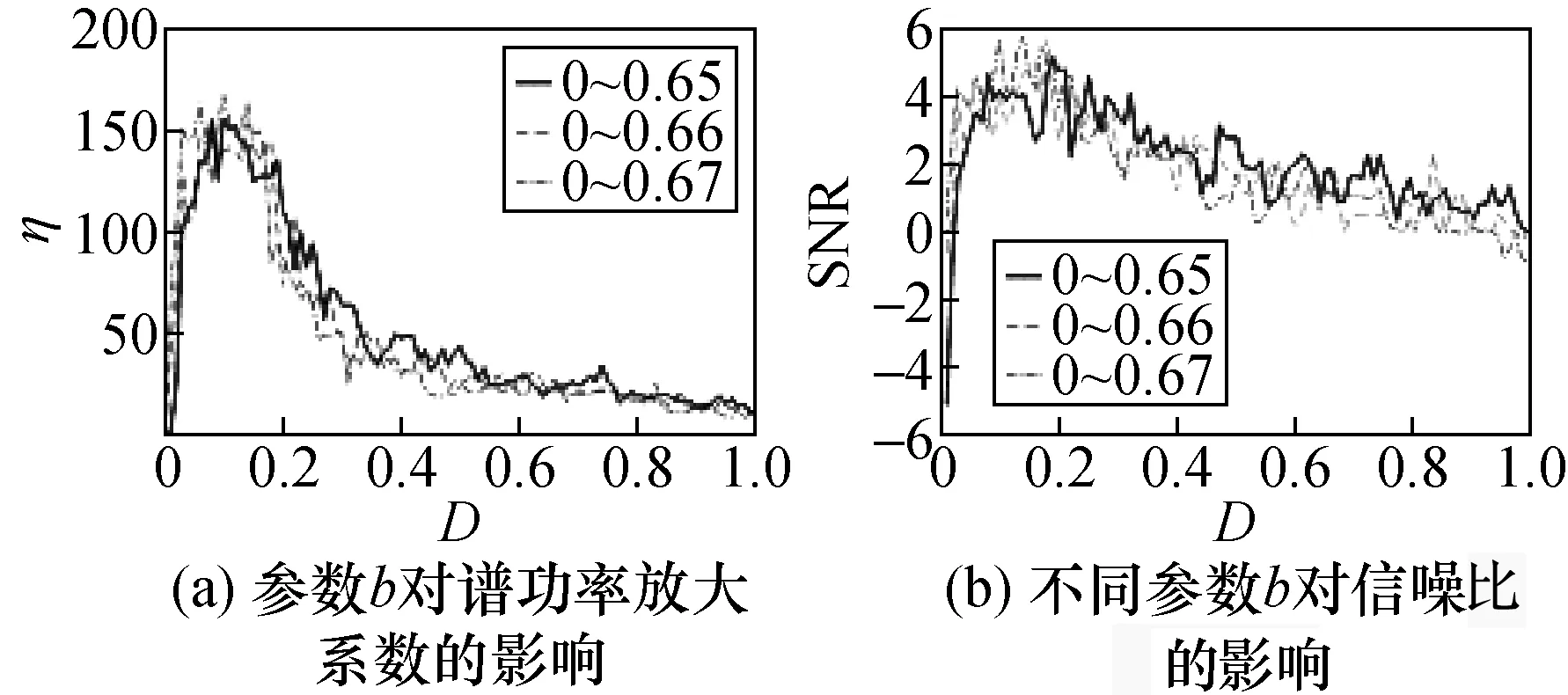
图2 在τ=2.4下,η和SNR随噪声强度的变化曲线Fig.2 The curves of η and SNR with noise intensity at τ=2.4
因此,选择极大值最大时的b=0.67,此时的SNR和η的值都达到最大,输入的模拟信号通过一般多稳随机共振(TSR)系统、基于时延反馈的多稳随机共振(TFTSR)系统和基于一次项时延的随机共振(LTFTSR)系统的频域图如图3所示。模拟信号经过TFTSR模型之后,驱动频率处的幅值从0.351增加到1.657,比经过TSR模型之后的驱动频率处的幅值增加了3倍。但是,通过比较图3(d)和图3(f)可以看出:LTFTSR系统比TSR系统能更好地提取驱动频率,并且驱动频率处的幅值从0.351显著提高到2.581。同时,通过LTFTSR的信号波形比通过TFTSR的信号波形更接近驱动信号,幅值也增强,这表明LTFTSR系统将更多的噪声能量传递给驱动信号能量,降噪的能力更强。
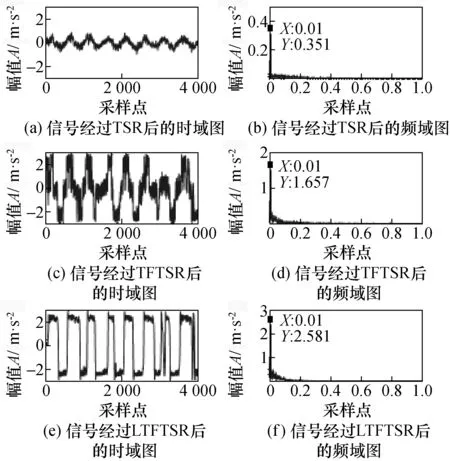
图3 各SR模型作用后的时域图和频域图比较Fig.3 Comparison of time-domain and frequency-domain diagrams of SR models
5 实例研究
5.1 美国西储大学实验数据
采用美国西储大学的轴承故障数据,实验台电机的转速为1 797 r/min(29.95 Hz),根据实验轴承的详细尺寸可以计算出轴承内圈故障频率的理论值为162.18 Hz。对于大频率的故障信号,采用变尺度的方法进行随机共振变换,二次采样频率为5 Hz。轴承内圈故障原始信号的波形图和频谱图如图4所示。图4中的高频率处的幅值是轴承部件的第1次自然模式振动引起的,因此在原始信号的频谱图中看不到明显的故障信号特征。
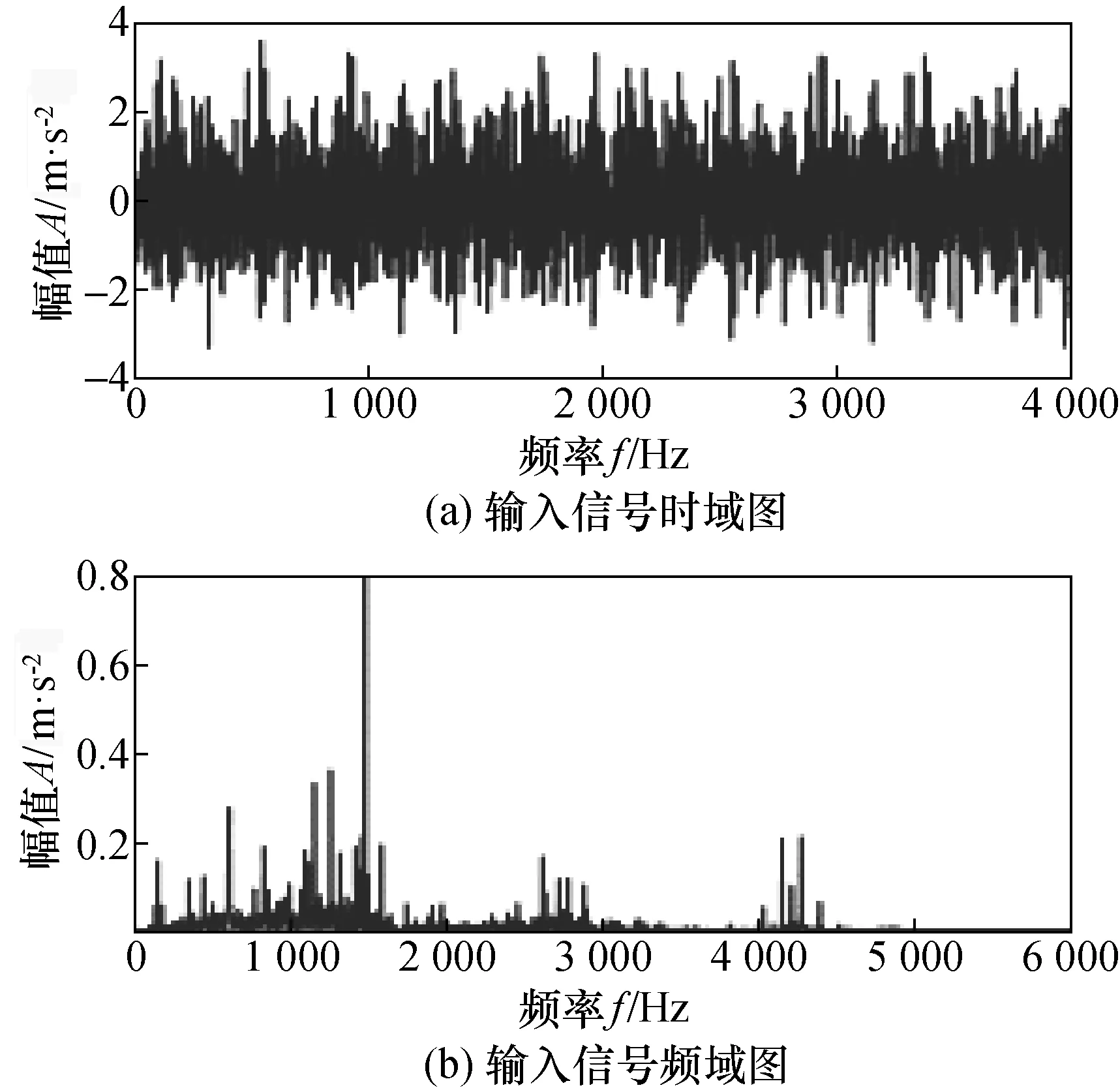
图4 轴承内圈故障原始信号的时域图和频域图Fig.4 Time domain and frequency domain diagram of the original signal of bearing inner ring fault
通过观察图5,经过SR系统后的内圈故障的频率为162 Hz,接近理论值162.18 Hz。比较图5(a)、图5(c)和图5(e)得到,LTFTSR系统的波形比TSR系统和TFTSR系统的波形具有更小的毛刺,也更接近正弦波形,并且振幅更清晰地集中在-3到3之间。在图5(d)中,SNR从1.39增加到2.13,η从2.77增加到19.73。这表明,噪声向故障信号传递了更多的能量,在故障频率处增大了信号的幅度,并通过TFTSR系统将其凸显在频谱中,但同时也增加了其它频率的振幅。从图5(f)中可以看出,LTFTSR系统的故障频率处的幅值高于TSR系统故障频率处的幅值,从0.700 5增加到1.945,仅特征频率处的振幅集中增加,其它混淆的频率分量大部分消除。SNR从1.39增加到5.66,η从2.77增加到152.03。具体的数据对比如图6所示。
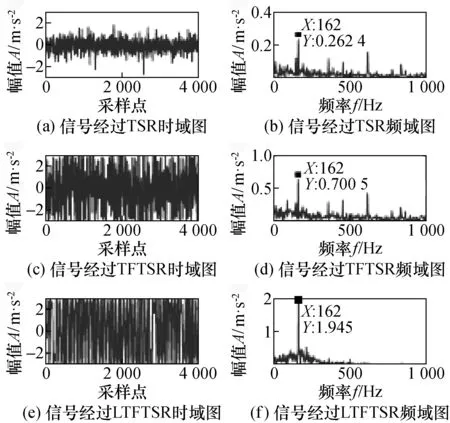
图5 不同SR模型作用后的内圈故障时频图Fig.5 Time-frequency diagram of inner ring fault after different SR models
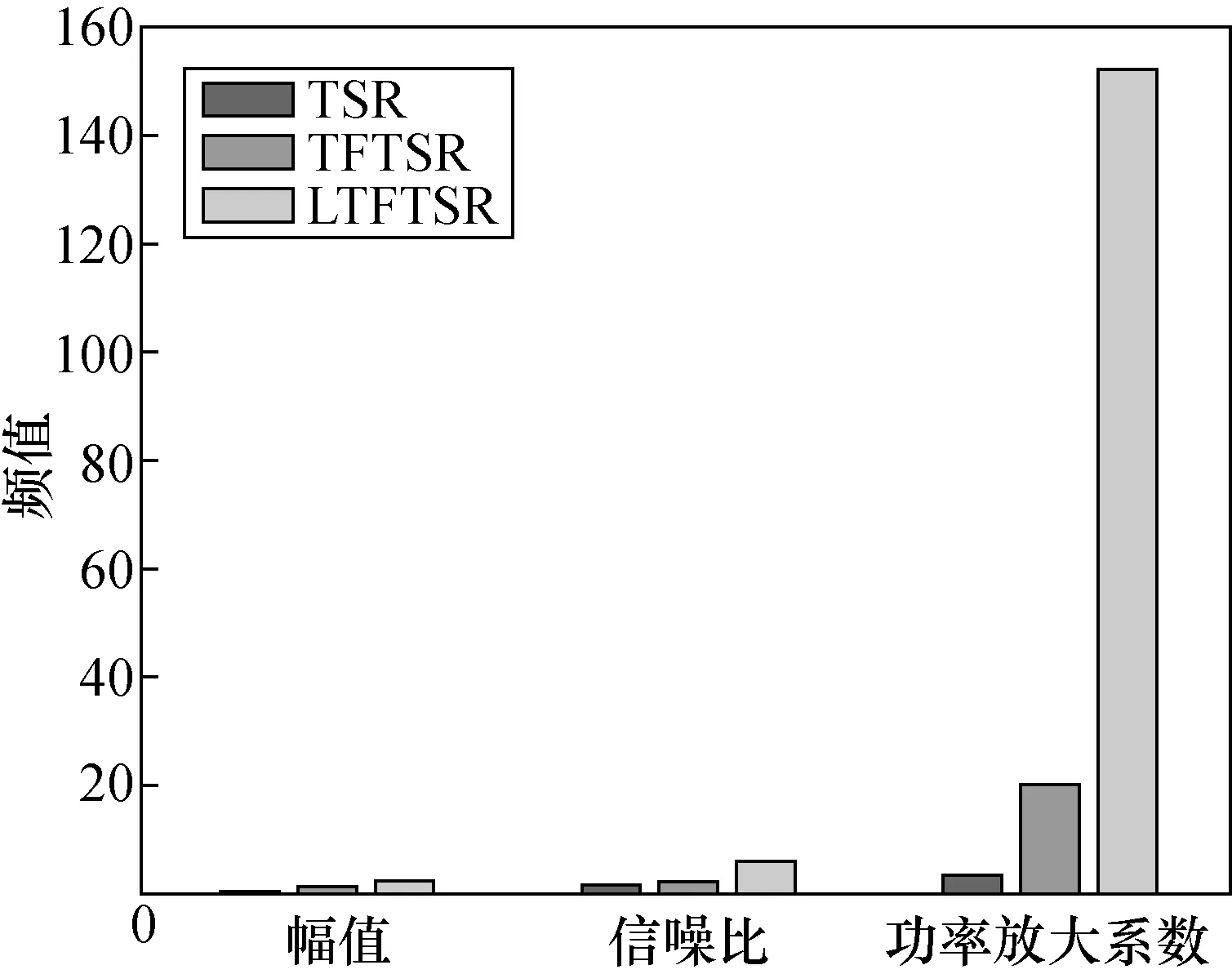
图6 3种SR模型处理信号后的对比图Fig.6 Contrast diagram after signal processing by three SR models
5.2 某公司实验数据
采用某公司的轴承实验工况29数据,经计算轴承外圈的故障频率的理论值为41.435 Hz。对该数据进行了3种SR模型降噪处理,并进行了对比,如图7所示。
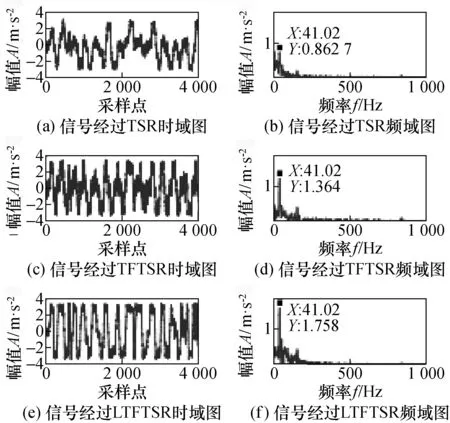
图7 不同SR模型作用后的内圈故障时频图Fig.7 Time-frequency diagram of inner ring fault after different SR models
可以看出,在图7(f)中的故障频率附近干扰频率的幅值较低,经过LTFTSR系统后的故障频率在频谱图中更突出,幅值从0.862 7增加到1.758。SNR从0.52增加到3.88,η从11.67增加到48.47。与图7(d)的频域相比,故障频率处的幅值从0.862 7增加到1.364,SNR从0.52增加到1.02,η从11.67增加到29.16。此外,通过观察3个波形图,发现图7(e)中的信号比图7(a)和图7(c)中的信号噪声更小且更规则,并且其波形更接近于周期性正弦波信号。数据比较如图8所示,综上所述,本文提出的方法在弱信号检测中具有优越性。
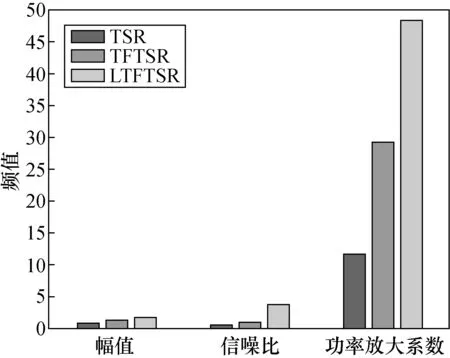
图8 3种SR模型处理信号后的对比图Fig.8 Contrast diagram after signal processing by three SR models
6 结 论
本文提出基于一次项时延的多稳随机共振模型早期微弱信号检测方法,进行了机理上的分析,通过模拟信号和实例信号验证,可知提出的一次项时延反馈多稳态随机共振模型有效地改进了时延多稳随机共振的模型的不足,集中提高了检测信号故障频率处的幅值,增加了输出信号的信噪比和输出信号的能量,为下一步的特征提取奠定基础。
