基于POE的工业机器人标定方法

魏文锋 王 勇

（广州数控设备有限公司，广州，510530）

0 引言

工业机器人能够代替人类完成一些重复的、繁重的劳动工作，以及在危险场景下的各种工作，这对于解放生产力，提高生产效率有着重要意义[1]。随着工业机器人的应用场景不断丰富，工业机器人能够完成的工作也从简单到复杂：从最初的搬运与码垛机器人，到后来的喷涂与焊接机器人，再到目前的装配与加工机器人，工业机器人能完成的工作任务越来越复杂化和精密化。这样的发展趋势对工业机器人自身的精度和性能也提出了更高的要求。

1 工业机器人绝对定位精度的提高方法

由于制造装配以及实际使用环境带来的误差造成工业机器人实际模型与编程使用和控制器中的名义模型存在误差，该误差被称为工业机器人的绝对定位精度。如果工业机器人绝对定位精度在毫米数量级，就难以满足将工业机器人用于复杂加工和装配任务的需求，工业机器人绝对定位精度则需要得到提升。

一般可以通过以下两种途径提高工业机器人绝对定位精度：

1）从误差的源头上减少误差的产生。即：使用更先进的制造方法和装配方法，减少制造和装配误差。由于当前的制造水平和产品经济性的限制，此方法难以实施。

2）对已有误差进行补偿。即运动学标定与补偿法。该方法是使用先进的测量仪器对工业机器人末端位姿进行测量，将测量数据导入到建立的工业机器人误差模型中，采用算法辨识出误差，再把通过补偿算法得到的数据输入到工业机器人的系统参数中进行补偿，最终使工业机器人末端执行器实际位姿与期望位姿的误差减小，从而绝对定位精度得到提高。这种方法实施成本低，是提升工业机器人绝对定位精度的主要途径。

上述提到的标定技术可分为基于模型的标定和无模型的标定两类。工业机器人拥有更多自由度，标定补偿问题比数控机床要复杂，空间位姿多，且非线性，对其标定需采用基于运动学模型的标定补偿方法。目前工业机器人建模方法有多种，最经典的模型是D-H模型，以及基于D-H模型衍生出来的建模方法[2-3]。

陈庆诚[4]指出D-H模型不满足完整性，因为其中的全部4个参数都是描述关于X轴和Z轴的运动，没有描述关于Y轴的运动。Hayati[5]在研究中发现，当D-H模型中因误差出现相邻Z轴交错的情况时，4个描述连杆的参数将会变得巨大以至于无法补偿，即出现奇异性问题。针对这一问题，Judd[6]建立了具有5个参数的MDH模型，相较于传统的D-H模型，该模型具有一个附加的旋转参数，但实验结果反映奇异性并未被彻底消除。Schroer K[7]等人针对冗余性对传统D-H模型进行处理，但在实验中，只有少部分的位姿得到辨识，此外迭代过程收敛慢，且易发散。

因为D-H方法以及基于其改进的方法在标定中都存在问题，后来研究人员基于旋量代数理论建立指数积公式法（Product-of-Exponential），简称POE法。杨向东等人[8-9]认为采用POE法建立的标定模型具有完整性、无冗余性、无奇异性。杨桂林[10]对POE法进行改进，提出局部指数积公式法（Local Product-of-Exponential，LPOE），并通过仿真与实验验证了方法的有效性。

2 基于POE工业机器人建模

2.1基于LPOE的工业机器人运动学模型

指数积模型由Brockett[11]提出，该模型需要建立两个坐标系：机器人基坐标系{B}和末端工具坐标系{T}。表示机器人零位状态下工具坐标系{T}相对于基坐标系{B}的齐次变换矩阵。为 第个关节的旋量在基坐标系{B}的表示， 为第 个关节的旋转角度（若是移动关节则表示位移量）。由此得到串联n自由度机器人正运动学模型为：

LPOE公式是在全局POE公式的基础上演变而来。首先将式（1）机器人POE公式写成齐次变换矩阵相乘的形式：

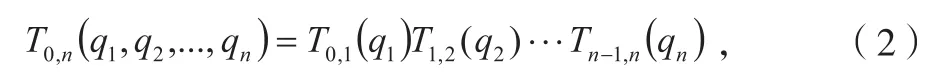
其中，Tn-1,n表示坐标系n相对于坐标系n-1的齐次变换矩阵；每个齐次变换矩阵改写为初始的齐次变换矩阵与关节旋量指数映射相乘的形式为：

然后得到n自由度串联机器人局部POE模型：

局部POE模型的特点是需要在各个连杆建立局部坐标系，虽然坐标系的建立较传统D-H法简便，但是这一特点使得局部POE模型可以应用在存在多个运动链的树形机器人上。

下面以广州数控RB08工业机器人为例，建立其运动学模型为：

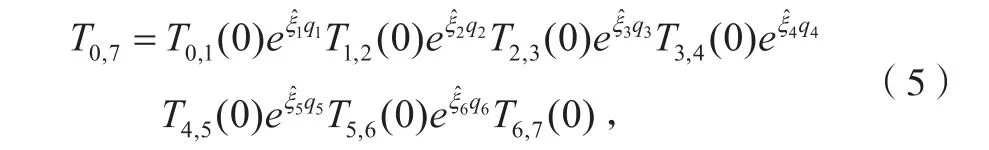
如图1所示，在广数RB08机器人的各个关节轴线上均建立局部坐标系，单位mm。

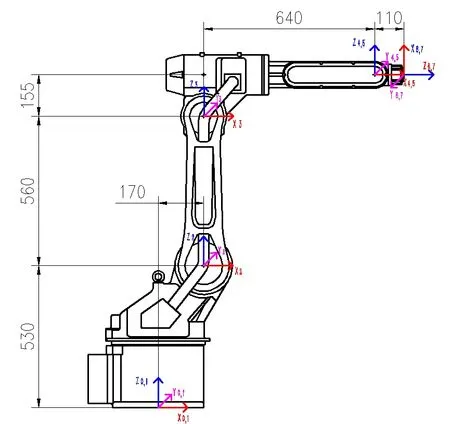
图1 广数机器人RB08局部坐标系

然后，应用MATLAB软件对上述所建立的广数机器人局部POE模型进行验证。

经验证，本文所建立的广数机器人LPOE模型与机器人示教器内的位姿一致，说明本节建立的局部POE机器人正运动学模型正确。

2.2工业机器人标定模型

为了得到一个对串联工业机器人可以通用的标定模型，在建模过程时，不针对某个特定机器人型号，所建立的标定模型对n自由度串联机器人普遍适用。

在下述公式推导过程中，涉及到的上标符号含义是：上标a表示实际值（测量值），上标c表示标定值，不带上标的表示名义值（理论值）。

结合式（4）、式（5），将n自由度串联机器人运动学模型改写为：

式（12）可写为线性方程组的形式，从而通过最小二乘法对参数进行辨识。

3 工业机器人误差标定仿真实验

3.1仿真方法

本节使用MATLAB编写标定程序，然后仿真模拟整个标定过程，通过仿真验证本文建立的标定模型和标定算法的正确性。

本节标定过程仿真的对象为广数RB08型工业机器人。

在广数工业机器人局部POE正运动学模型中，连杆坐标系初始变换矩阵T(0)改写为矩阵指数形式：

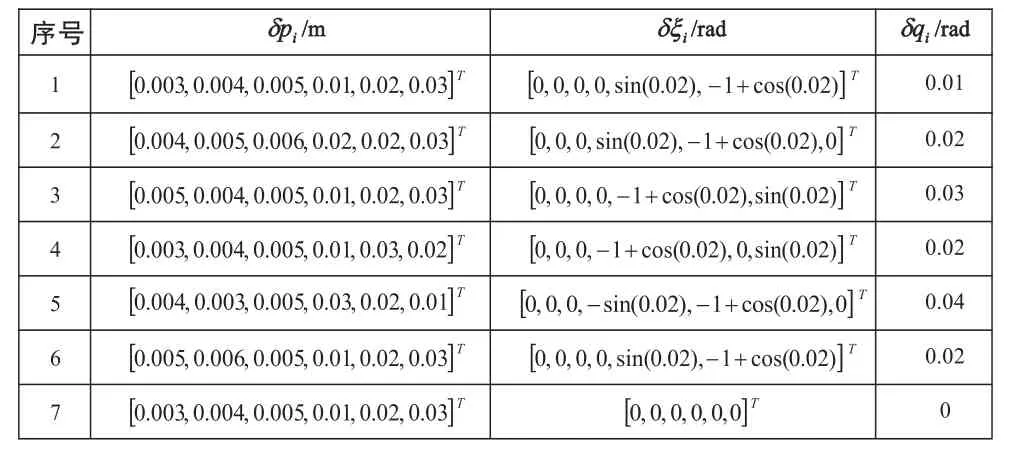
表1 预设的几何参数误差

同时，还需满足条件：

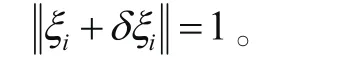
关节角度误差量级为0.01rad，表示实际关节转角有约1°的偏差。仿真所设置的误差均大于实际情况的误差，由此验证了本标定模型具有实际应用能力。

3.2标定误差评估方法

3.3仿真结果分析

为了说明标定的模型在整个机器人工作空间都有良好的精度，笔者在机器人各关节转动范围内随机选取100组关节转角，进行100个位姿评估，计算标定位姿与实际位姿的量化偏差，具体评估结果如图2所示。

100个评估点的量化位置偏差平均值为6.47e-12m，最大值1.24e-11m，量化方向偏差为0。对于此100个点的上述3个误差进行评估，评估结果说明：仿真标定辨识出了机器人的几何参数，得到了精度远高于机器人定位精度要求的运动学模型，验证了本标定模型与标定算法的有效性。

图2 100个随机评估点量化位置偏差

4 误差影响规律分析

上述进行的仿真是基于完全精确的机器人末端位姿测量数据进行的，然而在实际实验中，由于测量仪器的误差以及机器人运动重复性带来的误差，机器人实际末端位姿无法精确地得到。为了验证标定方法在现有的测量精度水平下的标定的能力，下面在仿真中引入误差。

带有误差的末端位姿测量数据，计算公式如下：

实验首先使用30个测量位姿进行仿真，迭代次数设置为6次。

加入测量误差后，笔者发现，迭代收敛速度不变，进行两次迭代，偏差数值就达到稳定，最终偏差数值稳定在与设置的实验误差相同的量级上。所以，笔者得出结论：最终标定模型的精度取决于仪器的测量精度和机器人重复定位精度。

根据最小二乘算法的原理，实验中使用越多的数据，标定结果将越精确。为了找到合理的实验使用数据量，下面通过仿真寻找实验使用位姿数m与标定得到的运动学模型精度之间的关系。

位姿数m从7到100，同样使用100个随机的位姿，评估其平均量化位置偏差与平均量化方向偏差，结果由图3、图4所示。

图3 量化位置偏差与实验使用位姿数关系

图4 量化方向偏差与实验使用位姿数关系

分析图3、图4可知，100个评估点的平均量化位置偏差与平均量化方向偏差，随着实验使用机器人位姿数量的增多而减少，最终稳定在约10-4rad，即标定实验中测量的数据越多，得到的运动学模型越精确。

实验数据表明：位姿数30以内误差下降迅速，因此标定实验使用的位姿数至少应为30个；位姿数70以上，偏差基本稳定，再增加测量数据对于标定模型精度的提高作用微小。故综合考虑，标定实验使用的测量位姿数在30～70个较为合理。

5 结论

本文首先基于工业机器人的局部POE运动学模型推导出工业机器人运动学标定模型，然后根据标定模型设计出运动学标定迭代最小二乘算法，最后编写MATLAB标定程序，对整个标定过程进行仿真。

在仿真的过程中，首先模拟使用无误差的测量数据进行标定，发现标定的运动学模型误差在工业机器人定位问题中可忽略不计，验证了运动学标定模型和标定算法的正确性。随后模拟引入带有实验误差的测量数据，发现最终标定出的运动学模型精度与引入的测量误差量级相当，证明了所建立的标定模型和标定算法在现有测量精度下实际应用的能力。最后通过研究标定出的运动学模型精度与标定实验所用测量位姿数关系，找到合理的实验测量位姿数，为后续标定实验的开展提供了一定的指导。