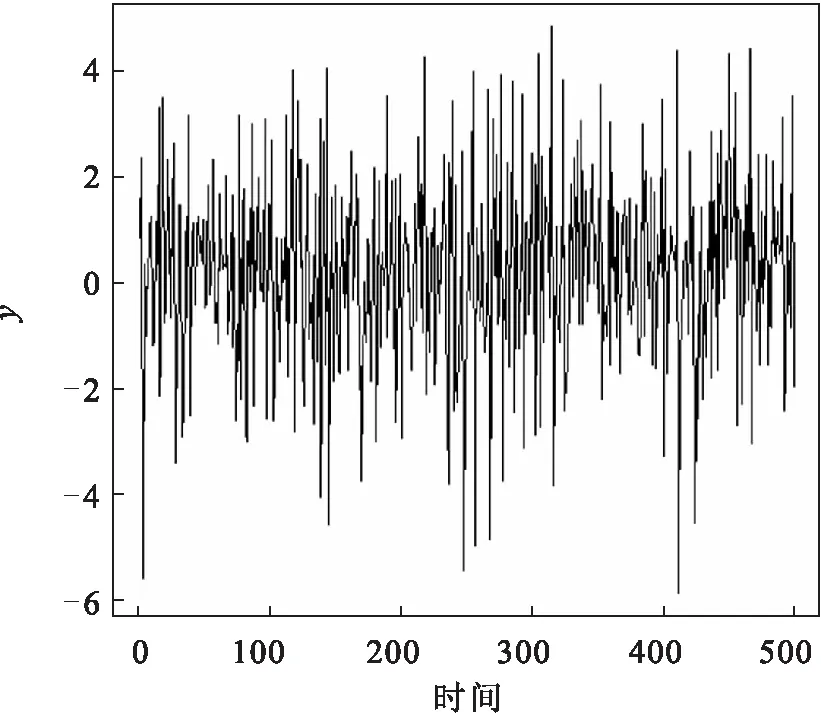
基于Gibbs抽样门限自回归模型的参数估计
2020-08-07郑月晨张慧增
蒋 捷,郑月晨,周 浩,张慧增
(杭州师范大学理学院,浙江 杭州 311121)
门限自回归(threshold autoregressive, TAR)模型是典型的非线性参数模型,可分为冲量门限自回归(momentum-TAR, MTAR)模型和自激励门限自回归(self-exciting TAR, SETAR)模型[1].在经济学研究中,很多与经济相关的时间序列大部分都具有非线性特征,如股价指数和汇率等.在处理非线性问题时,建立传统的线性时间序列模型不能充分地提取数据信息,从而也显示出了线性模型的局限性.SETAR模型是基于不同的门限变量把整个时间序列分为若干个小段(体制),在每个体制上用AR(autoregressive)模型去线性逼近,把全局空间上的非线性时间序列模型转化成子空间上的线性模型.虽然二体制的TAR模型形式简单,最小二乘法也可以估计出模型参数,但繁琐的过程和估计精度很难应用到具体问题中.对于TAR模型,蒙特卡洛模拟(Markov Chain Monte Carlo,MCMC)方法不仅可以相对快速地估计出模型参数,还可以提高估计的精度,实施起来也比较便捷.本文运用了Gibbs抽样,在机器学习中,很多情况无法确定一个概率分布的具体密度函数,只是知道样本其中一个属性在其他所有属性下的条件概率,而Gibbs抽样正是解决此类问题的方法之一.TAR模型的参数估计方法主要分为以下几种:一是最小二乘法结合赤池信息量(akaike information criterion, AIC),但此方法计算量大且繁琐,很难推广并且实现;二是Tasy提出的F统计量以及t统计量来选择各参数的值;三是利用MCMC方法.本文利用MCMC算法与Gibbs抽样,可避免繁琐的迭代以及复杂的似然比检验,对模型的选择和参数的估计实施更为快捷有效.
1 门限自回归模型及其参数的贝叶斯估计
1.1 门限自回归模型
若y={yt,t=1,2,…}为一时间序列,满足以下结构的时间序列模型称为门限自回归模型,记为TAR(k,p1,p2,…,pk):
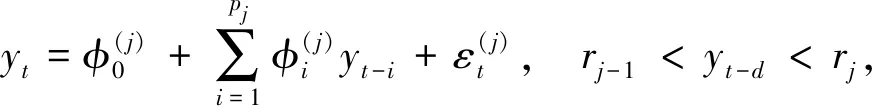
(1)

下面以二体制(即k=2)的门限自回归模型TAR(2,p1,p2)来说明TAR模型的参数估计,即
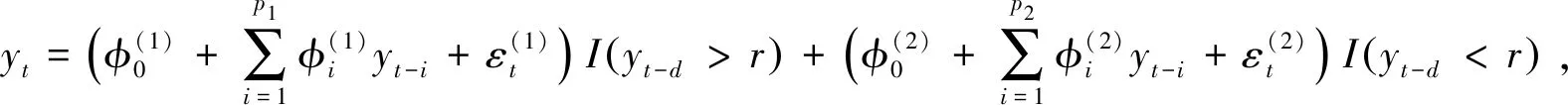
(2)
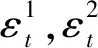
设∃p∈N*,使得0≤p1,p2,k=2,d≤p,{y1,y2,…,yp}为时间序列{yt}的前p个观测值.把{yp+1,yp+2,…,yn}向前移动d个单位,令πi为移动后新时间序列的第i个观测值,即yπ1 f(Y|Φi,σ2,r,d;i=1,2)= (3) 为了解决当数据维数增加时计算和书写变复杂的问题,把式(3)写成矩阵相乘的形式.令 则式(3)可写为 (4) 贝叶斯学派与频率学派的主要差异在于:前者利用收集到的先验信息,形成先验分布,在给定样本分布和先验分布之后,运用贝叶斯公式计算待估参数的后验分布.在求得后验分布后,模拟该分布生成的随机数[4],若把随机数看成样本,则用样本均值和样本方差来估计与评价待估参数. 设(Φi,σ2,r,d)的先验分布为π(Φi,σ2,r,d),由条件概率公式可知 π(Φi,σ2,r,d)=π(Φi|σ2,r,d)·π(σ2|r,d)·π(r|d)·π(d). (5) 由式(4)和(5)可求得(Φi,σ2,r,d)的后验分布 (6) 设θ是总体分布的参数向量,π(θ)是参数向量θ的先验分布,若后验密度函数与π(θ)有相同的密度函数形式,则π(θ)称之为参数向量θ的共轭先验分布.根据共轭先验分布的特点,因为Φ1,Φ2相互独立,可以得到Φi的条件后验分布 (7) σ2的条件后验分布: (8) r的条件后验分布: p(r|Y,Φi,σ2,d)∝exp(-s2/2σ2)I(a (9) 其中I表示示性函数. 后验分布包含了对参数的信息,如均值、方差,但很多情况无法确定一个概率分布的具体密度函数,或密度函数太复杂,只是知道样本其中一个属性在其他所有属性下的条件概率,此时上述后验分布正好满足这样的要求,所以对每个参数的估计可以通过Gibbs抽样来实现. Gibbs抽样是一种特殊的MCMC算法[5],主要用于状态空间为乘积空间的情况.往往在待估参数维数较高的情况下,贝叶斯统计推断更倾向于求出总体对某参数的条件分布,Gibbs抽样方法适用于条件分布比边缘分布更容易求得的情形.该方法每次只更新状态的一个分量,这样就能把高维抽样转化为低维抽样的问题.对于TAR模型的Gibbs抽样步骤如下: 作为上述方法的检验,超参数的选取为:Φ1~N(0,0.2),Φ2~N(0,0.2),σ2~IG(1.2,0.5),r~U[p5,p95][6],d服从1,2,3上的离散均匀分布;其中p5,p95分别表示数据的第5和第95个百分位数,εt~N(0,σ2),以TAR(2,1,1)模型为例: yt=[1+0.5yt-1I(yt-d<0.6)]+[1-0.9yt-1I(yt-d>0.6)]+εt (10) 生成500个模型(10)的数据,数据时序图如图1所示. 图1 生成样本的时序图Fig.1 Sequence diagrams of sample generated 表1 被估参数模拟结果Tab.1 Simulation results of parameters 利用上述生成的数据,用Gibbs抽样方案进行迭代,被估参数的后验均值和后验方差如表1所示.表1记录了模型(10)各个参数的真实值、后验均值和标准误. 根据贝叶斯统计推断,通过先验分布(共轭先验分布),对TAR模型中各参数的后验分布进行分析推导,同时利用MCMC算法与Gibbs抽样解决了参数从高维到低维的合理性转变,提高了估计精度.最后的数值模拟得到的结果也与真实值偏差较小,说明该方法是有效的.



1.2 基于贝叶斯分析下TAR模型的参数估计



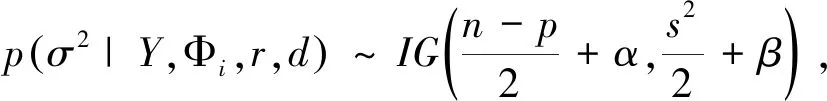



2 Gibbs抽样
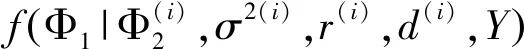

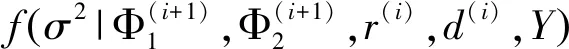
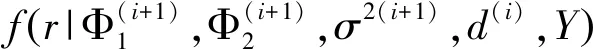
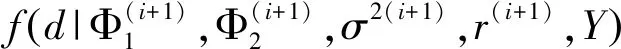
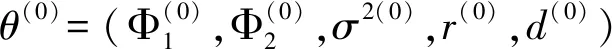
3 数值模拟


4 结论
