深基坑h型双排桩的变形计算及优化分析

罗忠行，牛建东，李泽玮，李姝，王克宏

深基坑h型双排桩的变形计算及优化分析

罗忠行1，牛建东2，李泽玮2，李姝2，王克宏1

(1. 湖南省核工业地质局三0三大队，湖南 长沙 410119；2. 中南大学 土木工程学院，湖南 长沙 410075)

针对目前深基坑工程中h型双排桩理论的不足，在考虑桩土非线性共同作用弹性反力法的基础上引入考虑非极限状态的土压力理论，得到一种可同时考虑非极限土压力理论和支护桩与土相互作用的支护结构水平位移计算方法。推导支护结构水平位移和地面沉降公式，研究深基坑开挖中h型桩支护结构的受力特性和变形规律。将理论成果应用于工程实例，与实测结果进行对比分析，并建立二维有限元模型，优化h型双排桩的设计参数。研究结果表明：支护结构水平位移与坡顶沉降均呈“匙”分布，桩间距为2倍桩径，排间距为5倍桩径，后排桩桩底标高略低于基底为较合理的设计参数。

h型双排桩；力学模型；受力特性；变形；有限元；设计参数

近年来，随着城市建设的快速发展，大量的深基坑分布在城市中心建筑物比较密集的地区。周边会有很多相邻建筑物、街道、地下管线、地下设施。基坑周边环境条件不仅限制了支护结构的设计、施工，而且对基坑开挖提出严格的变形要求[1−2]。在这种情况下，h型双排桩支护体系在基坑工程中也逐渐得到了应用。在滑坡支挡、高边坡以及膨胀土边坡领域，h型抗滑桩能够增大支护结构侧向刚度，有效限制坡体侧向位移，目前很多学者[3]对h型抗滑桩做了较多研究。欧明喜[4]在研究双排抗滑桩受力机理的基础上，通过理论分析、模型试验、数值模拟及工程应用，对h型抗滑桩的受力机理进行了研究。王羽[5]针对ｈ型抗滑桩支护结构，在分析其受力机理的基础上，提出了相应的结构计算和设计的理论方法。李洋等[6−7]通过室内模型试验结合数值模拟的方法，研究了ｈ型抗滑桩的受力机制，并对其几个设计参数进行了优化。杨晓珊等[8−9]以湘南某红层滑坡工程治理为例，对h型抗滑桩的受力特性和变形进行了数值模拟，并详细分析了桩排距、连梁刚度和嵌固深度等参数对结构支护特性的影响；许佳佳等[10]采用数值分析方法结合工程实例对h型桩板墙桩土相互作用进行了分析，认为连系梁对主桩起到了显著支撑作用，增强了主桩的抗滑能力。而在深基坑工程中，虽然h型支护排桩已经得到了较为广泛的应用，但是其设计和施工往往凭借经验或者借鉴抗滑桩的设计施工方法，理论研究远远落后于工程实际。申永江等[11−12]重点分析了门式双排桩前后桩排距的变化对结构体系内力及变形的影响。夏彪[13]通过研究双排桩在基坑工程中的变形特性，并与实测结果进行了对比来侧面反映h型双排桩的受力性能。侯大伟等[14−15]在忽略桩土竖向摩擦效应和空间效应的基础上，根据 Winkler地基梁模型对双排桩支护体系的受力机制进行了分析。综上所述，目前h型双排桩在基坑工程中还没有统一的计算模型[16]，许多设计者往往按照抗滑桩的设计方法结合工程经验或者直接采用双排桩的计算方法进行设计，这都会给实际工程带来许多不确定性。基于以上背景，本文通过理论分析，建立了h型桩在基坑工程中的力学模型，推导了支护结构与基坑周围土体的变形计算公式。同时将该理论成果应用于永州市某基坑工程中。最后建立数值分析模型，探讨总结了h型桩参数对支护结构变形的影响，为类似复杂深基坑的设计和施工提供参考。

1 结构构造

h型排桩由预应力锚杆和前排桩，后排桩以及桩间连梁构成，协同承担土压力。使得作用在结构上的坡体土压力一部分通过锚杆传至锚固体周围稳定土层，另一部分土压力通过桩体传至基坑底部以下稳定土层，其结构剖面如图1 所示。由于h型桩的上下2级支护结构通过连梁连接在一起，使其具有较大的桩身侧向刚度，显著增加其抵抗侧向变形的能力。研究表明，桩顶连梁能有效调整结构内力分布，减小桩身内力，使其受力分布更趋于合理，从而降低了支护成本。因此h型桩支护较传统桩锚支护结构受力更加合理，基坑支护更加可靠。

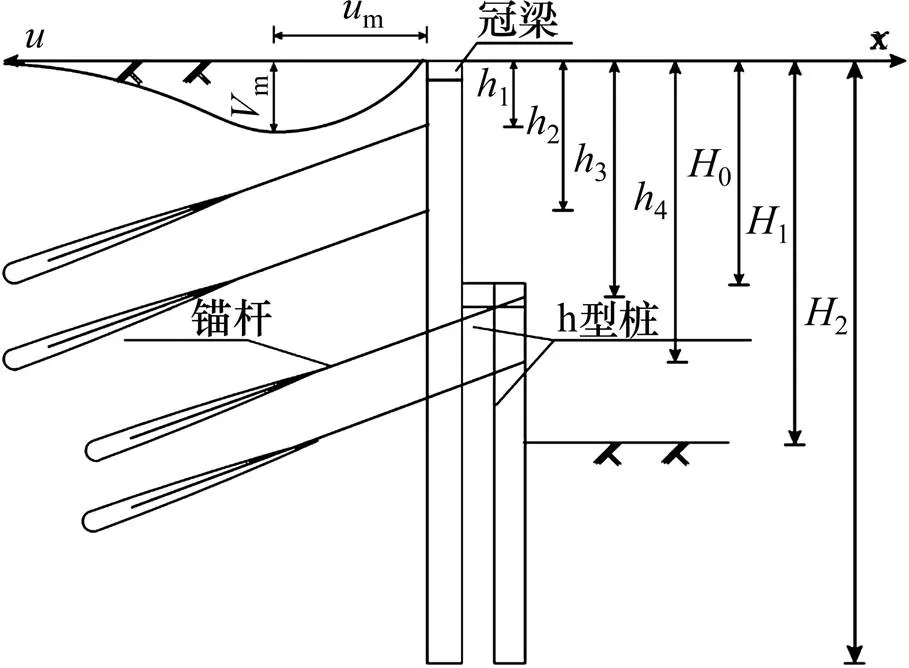
图1 h型桩支护结构剖面图

1.1 土压力动态分布

h型双排桩属于一种轻型的柔性挡土结构，作用在支护结构上的土压力不仅与支护结构背后土体性质有关，且与支挡结构及土体的位移和变形有关，图2给出了土压力随支护结构位移的变化。基坑开挖之前，支护结构上受到的土压力为静止土压力0，随开挖进行，支护结构上的土压力随位移发生变化，其大小等于静止土压力与土压力增量之和。且主动变形时，土压力增量为负；被动变形时，土压力增量为正。作用在支护结构上的土压力通常在a~p之间。本文用正弦和幂函数组成的复合函数表示与位移相关的土压力计算方法：

主动土压力：

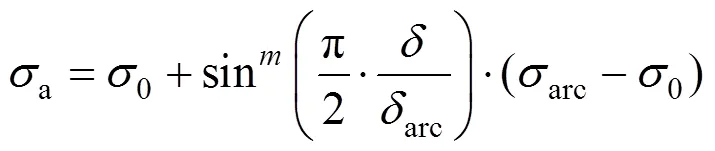
被动土压力：

其中：0为静止土压力；为土的位移(取正值)；acr为土的主动极限位移；pcr为土的被动极限位移；acr为极限平衡状态的主动土压力；pcr为极限平衡状态的被动土压力；为支护系数，随支护结构刚度、土体的性质及开挖深度有关，取0~1，当基坑参数及支护结构等不利于基坑稳定时，取上限。

由式(1)和式(2)，如果土体位移等于主动极限位移acr，计算得到的土压力就是主动极限土压力acr；如果土体位移等于被动极限位移pcr，计算得到的土压力就是被动极限土压力pcr。

图2 土压力随支护结构位移的变化

1.2 土的位移和变形

1.2.1 变形计算方法

考虑前后排桩变形协调，认为其变形相一致。根据弹性地基反力法中地基梁挠曲微分方程通式：

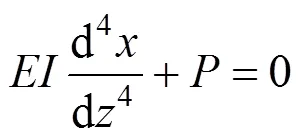
式中：为桩的抗弯刚度；为桩身水平位移；为计算深度；为作用于支护结构上的水平荷载 集度。

在现有的考虑非线性共同作用弹性反力法的基础上引入考虑变形的土压力计算公式，得到改进的弹性地基反力法。如图1所示，其中支护桩的挠曲微分方程为：

在计算作用于桩身的水平作荷载时，土压力强度由式(2)确定，锚杆对桩身的水平作用力则通过考虑锚杆变形与锚杆所在位置桩身的变形协调条件确定：

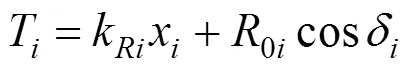
在不考虑冠梁或者腰梁的影响时，锚杆的刚度系数计算如下：

式中：k为锚杆刚度系数；E和E分别为锚杆的钢绞线弹性模量和复合弹性模量；A和分别为锚杆和注浆固结体的截面积；b为结构计算宽度；l和l分别为锚杆自由段和锚固段长度；为锚杆的水平间距；E为注浆固结体的弹性模量。

1.2.2 位移求解

1) 水平位移

求解式(4)挠曲微分方程，沿桩身长度方向以锚杆位置及基坑开挖面为界进行分段计算，并规定向基坑内侧方向变形为正，引入约束条件：

对h型桩顶部及底部有：

则

对锚杆位置处有：

2) 地面沉降

日本道路工程规范中，计算地面沉降时假定支护结构变形前后所围成的面积S与地面沉降曲线与原地面所围成的面积S相等，再根据支护结构的变形值来推求地面沉降大小。

计算模型假定地表沉降曲线为偏态分布：

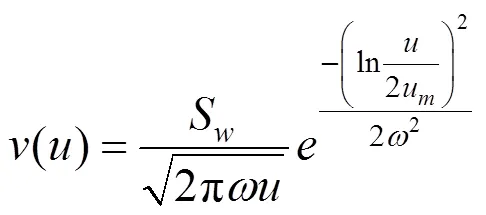
式中：为墙后任一点的地表沉降；为待求沉降点距坑壁距离；u为最大沉降点距坑壁距离；S为沉降曲线包络面积；为经验系数。

最大沉降点位置：

式中：为比例系数，当插入比(2−1)/1≤0.5时，可取0.5~0.6, 当(2−1)/1≥0.5时，可取0.6~ 0.7。

沉降包络面积S与支护结构变位曲线包络面积S有如下关系：

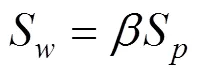
式中：为比例系数，当插入比(2−1)/1≤0.5时，可取1.0~1.2, 当(2−1)/1≥0.5时，可取 0.8~1.0。

对支护结构侧向位移曲线积分可求得S：

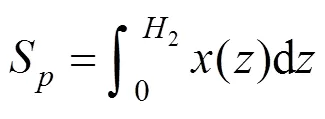
代入式(10)得到地表沉降估计：

2 工程实例和数值模型

2.1 工程概况

本工程位于永州市冷水滩区湘永路与双洲路交汇处东南角，基坑底标高约为93.0 m，正负零标高106.5 m，基坑南侧标高115.0 m以上为永久性边坡，边坡高度10.0~12.6 m。基坑深度为8.1~18.7 m，基坑边坡支护总高度8.1~23.8 m。

本基坑地层条件为软硬地层交替存在，主要由黏土、强风化泥灰岩，及下部中风化碳质泥灰岩组成。其中黏土层厚度较大，平均可达17.4 m。地下水类型为潜水，在基坑开挖以前，基坑内水位降到基底以下，故不考虑地下水的影响。场地各土层物理力学参数见表1。

表1 土层参数

2.2 基坑支护形式

由于该深基坑工程距离周边构筑物很近，基坑施工空间受限，此外对施工扰动和噪音的要求较高，同时还要严格控制基坑的变形位移。采用常规的桩锚支护，不仅受到地形的限制，对周边扰动较大，而且支护结构的变形得不到满足。采用地连墙＋内支撑的支护方案，施工扰动和变形得到了控制，但是斜撑、内支撑占用较大的空间，施工繁琐，不利于后续的施工。同时考虑到工期和经济因素，决定采用h型桩+锚杆的支护方案，本文选取如下典型剖面计算，设计参数如图3所示。

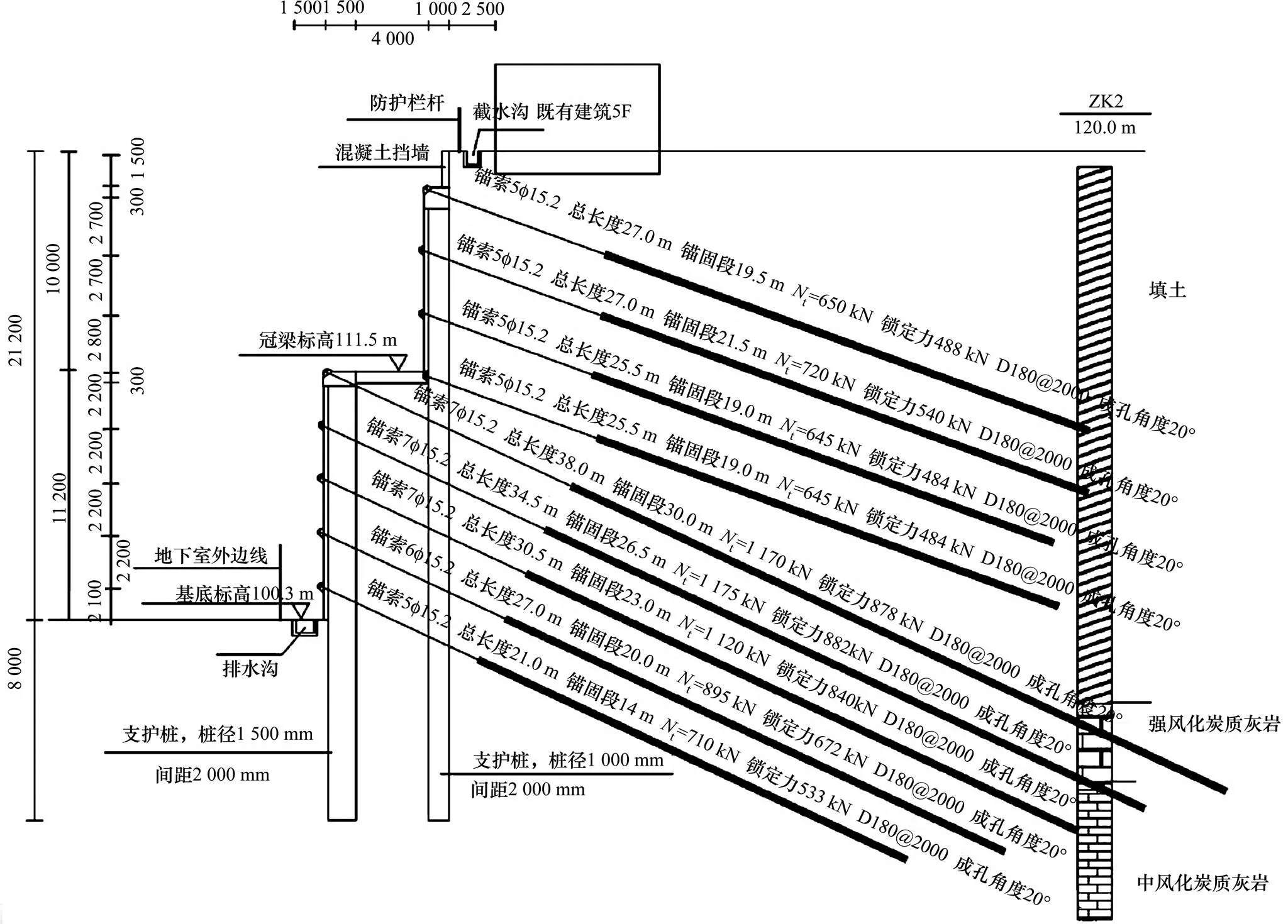
图3 基坑支护典型剖面图

2.3 二维模型的建立

为了研究h型桩的支护性能，同时了解基坑的变形特点和验证h型桩支护结构的合理性，利用MIDAS GTS建立h型桩的二维有限元分析模型。支护桩采用梁单元模型，锚杆采用植入式桁架模拟。模型尺寸120 m×60 m，本构模型采用摩尔−库仑理想弹塑性模型，土体模量借鉴Burland, St.John等的研究成果。Burland等认为实际土体的模量是室内固结不排水三轴试验值的3~5倍，并且随着深度的增加迅速增大。有限元模型如图4。

2.4 计算结果分析

图5和图6分别给出了支护结构侧向位移和基坑周围地表沉降的理论值、数值值和实测值。结果表明，本文计算模型得到的理论值与现场实测数据基本吻合，验证了模型的合理性。支护结构侧向位移沿开挖深度的增加表现出先增大后逐渐减小，最后趋于稳定的趋势，水平位移沿深度的总体分布为“匙”形。h型桩水平位移理论计算结果最大为13.20 mm，出现在距坑底9.5 m处，实际监测值为12.3 mm，数值模拟结果为17.65 mm。

图4 数值模型网格划分

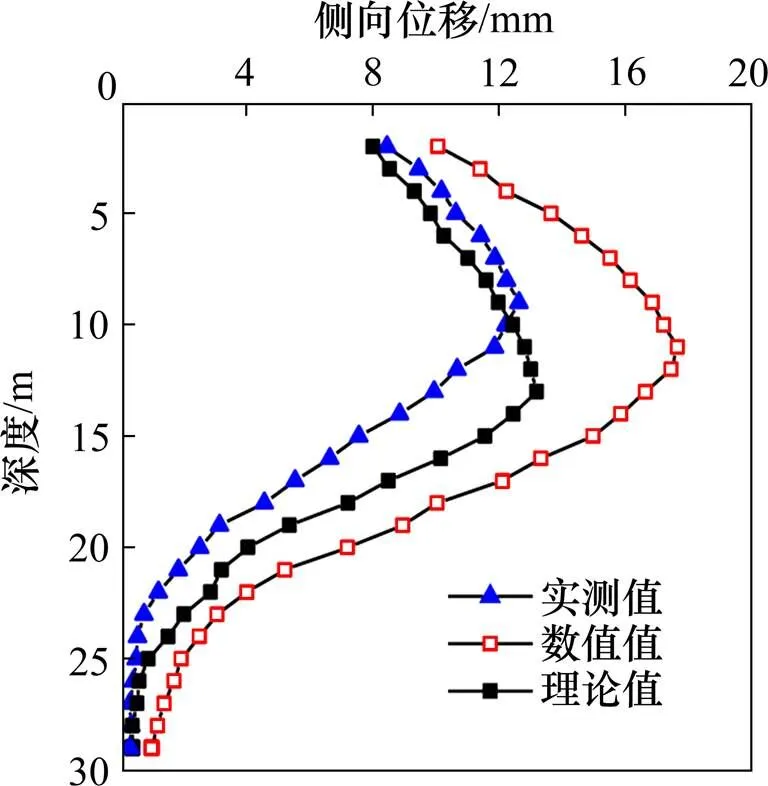
图5 支护结构水平位移对比

图6 基坑周围土体竖向位移对比

实测坡后地面最大沉降为13.52~15.24 mm，理论计算结果14 mm，数值模拟结果为16.23 mm。同时,基坑底部越靠近基坑中心,数值模拟结果略大于实测值，可能是参数取值和对本构模型假设所致。

3 h型桩的参数优化

3.1 桩间距

桩间距对h型支护桩的受力性能也有较大影响。桩间距过大，不能发挥土拱效应和群桩效应，过小则浪费材料经济效果不合理。通过固定h型桩的排间距和前后排桩高差Δ=0，改变h型桩桩间距分别为1~5倍桩径进行数值分析，得到支护结构桩身最大位移随不同桩间距的变化关系，见图7。由图7可知，随着桩间距的减小，桩身最大水平位移逐渐减小。桩间距从5倍桩径减小至2倍桩径时，后排桩身最大位移从30.6 mm 降至18.3 mm，前排桩身最大位移从31.5 mm 降至18.1 mm。桩间距小于2倍桩径时，桩身最大位移均减小，但减幅不大。因此本文得到h型桩支护最优桩间距为2倍桩径。

图7 不同排间距桩身最大位移

3.2 排间距

排间距是指经连梁相连的前后排桩形心之间的水平距离，排间距是影响ｈ型双排桩空间刚度的因素之一，也是桩间土发挥作用的重要因素。排间距过大不能形成土拱效应，无法充分发挥前后排桩之间的空间刚度作用，过小又不能发挥h型抗滑桩抗倾覆能力，而且经济不合理。取桩间距为2倍桩径，前后排桩高差Δ=0，改变排间距分别为3~7倍桩径进行数值分析，得到支护结构桩身最大位移随排间距的变化规律。

由图8可知，随着排间距增大，桩身最大水平位移逐渐减小，但是变化速率不同。排间距从3倍桩径增大至5倍桩径，后排桩最大位移从21.3 mm 降至16.3 mm，前排桩最大位移从20.9 mm 降至16.1 mm。排间距大于5倍桩径时，桩身最大位移也在减小，但减幅不大。因此本文得到h型桩最优排间距为5倍桩径。

3.3 前后排桩高差

在h型桩中，前后排桩的高差值也是影响支护结构受力性能的重要因素。通过设置h型桩的桩间距为2倍桩径，排间距为5倍桩径，改变前后排桩高差Δ，研究支护结构最大水平位移与前后排桩高差之间的关系。由图9可知，前后排桩的最大水平位移与h型桩前后排桩高差值Δ的大小呈正相关。随着前后排桩的高差减小，h型桩的水平位移逐渐减小。

图8 不同排间距桩身最大位移

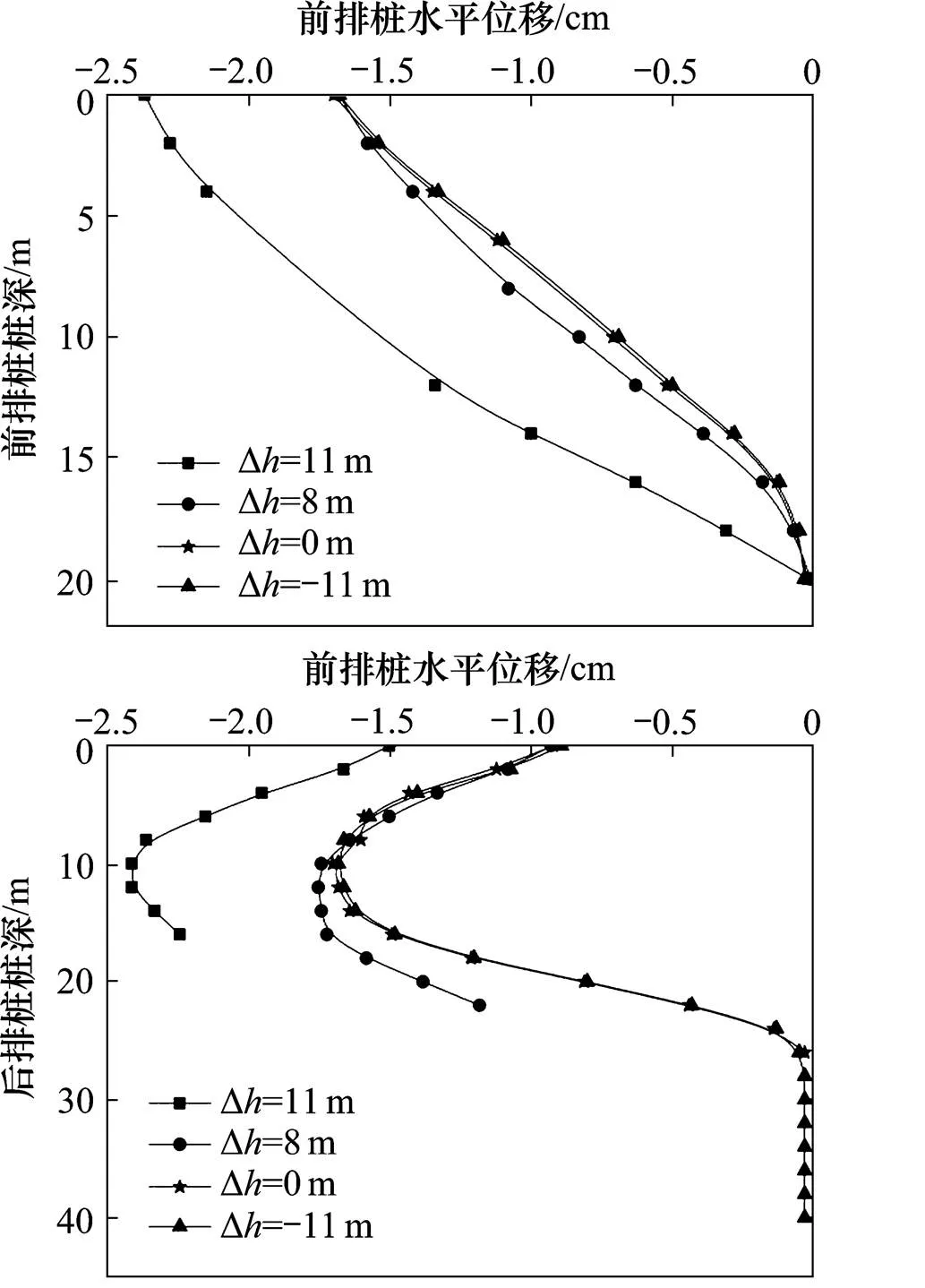
图9 前后排桩水平位移

当前后排桩高差由Δ=11 m减小为Δ=8 m(后排桩桩底标高与基底标高相等)时，支护结构最大水平位移由23.5 mm减小为16.35 mm。当后排桩桩底标高等于基底标高(Δ=8 m)时，前后排桩的水平位移达到较小值并趋于稳定。此时继续增大后排桩埋深，h型桩的水平位移变化不大。因此，为了使前后排桩水平位移得到有效控制，并且同时兼顾工程经济性的要求，应使后排桩桩底标高等于或略低于基底标高即可(Δ=8 m)。

4 结论

1) 基于弹性地基法和考虑位移的土压力计算方法，提出h型双排桩在基坑工程中的力学模型，对基坑变形进行求解，计算结果与实测值吻合 较好。

2) 得到h型双排桩的受力变形特性，支护结构水平位移随基坑深度呈先增大后减小的变化趋势，坡后竖向位移与距坑边距离在一定范围内也呈现“匙”形分布，超过30 m范围影响可忽略不计。

3) 通过有限元软件，采用单一变量法得到优化的h型双排桩设计参数。当桩间距为2倍桩径，排间距为5倍桩径，后排桩底标高略低于基底标高时，支护效果较为良好。

[1] 蔡宏环, 张立群, 赵国景. 深基坑开挖中双排桩支护的三维有限元模拟[J]. 岩土力学, 2006, 2(4): 662−666. CAI Honghuan, ZHANG Liqun, ZHAO Guojing. Numerical simulation of deep foundation pit excavation with double-row piles[J]. Rock and Soil Mechanics, 2006, 2(4): 662−666.

[2] 李连祥, 王兴政. 考虑基坑支护结构变形模式的土压力研究[J]. 地下空间与工程学, 2018, 14(4): 1024−1033. LI Lianxiang, WANG Xingzheng. Research on earth pressure considering deformation pattern of foundation pit supporting structure[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(4): 1024− 1033.

[3] 朱庆科. 深基坑双排桩支护结构体系若干问题分析和研究[D]. 广州: 华南理工大学, 2013. ZHU Qingke. Analysis and research on some problems of double row pile support structure system of deep foundation pit[D]. Guangzhou: South China University of Technology, 2013.

[4] 欧明喜. h型抗滑桩力学机理及其工程应用研究[D]. 重庆: 重庆大学, 2012. OU Mingxi. Research on mechanical mechanism and engineering application of h-type anti-slide pile[D]. Chongqing: Chongqing University, 2012.

[5] 王羽. h型抗滑桩设计计算方法研究[D]. 成都: 成都理工大学, 2011. WANG Yu. Research on design calculation method of h-type anti-slide pile[D]. Chengdu: Chengdu University of Technology, 2011.

[6] 李洋, 李元松, 王亚军. h型抗滑桩的受力特性及优化设计[J]. 武汉理工大学学报, 2016, 38(2): 173−177. LI Yang, LI Yuansong,WANG Yajun. Mechanical characteristics and optimization design of h-type antisliding pile[J]. Journal of Wuhan Institute of Technology, 2016, 38(2): 173−177.

[7] 张小丁. h形抗滑桩治理某红层滑坡的数值分析[D]. 衡阳: 南华大学, 2013. ZHANG Xiaoding. Numerical analysis of h-shaped anti-slide pile to control a red-bed landslide[D]. Hengyang: University of South China, 2013.

[8] 杨晓珊, 莫海鸿, 陆兆成, 等. 带斜撑h型抗滑桩的力学机理研究[J]. 四川建筑科学研究, 2013(8): 160−164. YANG Xiaoshan, MO Haihong, LU Zhaocheng, et al. Simulation on deep foundation pit in complex environment research on mechanical mechanics of h-type anti-slide pile with diagonal racing[J]. Sichuan Building Science, 2013(8):160−164.

[9] 文行武. 长短双排支护桩的简化算法及应用[J]. 福建建设科技, 2015(1): 9−10, 4. WEN Xingwu. Brief calculation and application of double row soldier piles with different length[J]. Fujian Construction Science & Technology, 2015(1): 9−10, 4.

[10] 许佳佳, 王晓健. h型抗滑桩加固边坡的优化分析[J]. 水电能源科学, 2016, 34(2): 113−115. XU Jiajia, WANG Xiaojian. Optimization analysis of slope reinforced by h-type anti-sliding piles[J]. Water Resources and Power, 2016, 34(2): 113−115.

[11] 申永江, 杨明, 项正良. 双排长短组合桩与常见双排桩的对比研究[J]. 岩土工程学报, 2015(增2): 96−100. SHEN Yongjiang, YANG Ming, XIANG Zhengliang. Comparative study on double-row piles with different lengths several common anti-slide piles[J]. Chinese Journal of Geotechnical Engineering, 2015(Suppl 2): 96− 1001.

[12] 林鹏, 王艳峰, 范志雄, 等. 双排桩支护结构在软土基坑工程中的应用分析[J]. 岩土工程学报, 2010, 32(增 2): 331−334. LIN Peng, WANG Yanfeng, FAN Zhixiong, et al. Application and analysis of retaining structure with double-row piles in soft ground excavation engineering[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Suppl 2): 331−334.

[13] 夏彪. h型双排桩在基坑工程中的变形特性研究[D]. 衡阳: 南华大学, 2016. XIA Biao. Study on deformation characteristics of h-type double-row piles in foundation pit engineering[D]. Hengyang: University of South China, 2016.

[14] 侯大伟. 土体位移对支护结构土压力分布的影响[J]. 四川建筑, 2015, 35(2): 83−85. HOU Dawei. Influence of soil displacement on soil pressure distribution of supporting structure[J]. Sichuan Architecture, 2015, 35(2): 83−85.

[15] 陈奕柏, 柯才桐, 高洪波, 等. 考虑变位影响的刚性挡墙非极限土压力研究[J]. 岩石力学与工程学报, 2015, 34(5): 1060−1070. CHEN Yibo, KE Caitong, GAO Hongbo, at el. Non-limit state earth pressure against retaining wall considering influence of deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 1060−1070.

[16] HUANG H, QUAN Z, LIU B L. Mechanical behavior and influencing factors of different pile-anchor supporting structures[J]. Journal of Highway and Transportation Research and Development, 2016, 10(3): 41−50.

Deformation calculation and optimization analysis of h-type double-row piles in deep foundation pit

LUO Zhongxing1, NIU Jiandong2,LI Zewei2, LI Shu2, WANG Kehong1

(1. 303 Brigade of Hunan Nuclear Geology, Changsha 410119, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

This paper aims at the theoretical defects of h-type double-row piles in deep foundation pit, the theory of soil pressure considering non-limit state was introduced on the basis of the elastic reaction method considering the nonlinear interaction. A method for calculating the horizontal displacement of supporting structure considering the non-limit soil pressure theory and the interaction between supporting pile and soil was proposed. The formulas of horizontal displacement and ground subsidence of the supporting structure were derived. Finally, the theoretical results were applied to engineering practice and compared with the measured results. A two-dimensional finite element model was established to optimize the design parameters of h-type double-row piles. The results show that the horizontal displacement of the supporting structure and the settlement of the top of the slope are distributed in a spoon distribution. The pile spacing is 2 times the pile diameter, and the row spacing is 5 times the pile diameter. The reasonable design is that the bottom elevation of the backrow pile is slightly lower than that of the base.

h-shaped double row pile; calculation model; mechanical characteristics; deformation; finite element; design parameters

10.19713/j.cnki.43−1423/u.T20200241

TU47

A

1672 − 7029(2020)07 − 1720 − 08

2020−03−29

国家自然科学基金资助项目(51778634)；国家级大学生创新训练资助项目(GS201910533226)

罗忠行(1965−)，男，湖南隆回人，高级工程师，从事地质灾害治理技术研究；E−mail：417028912@qq.com

(编辑 蒋学东)