高速铁路大跨度混凝土斜拉桥设计研究
2020-08-07龚俊虎
龚俊虎
高速铁路大跨度混凝土斜拉桥设计研究
龚俊虎1, 2
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2. 中铁磁浮交通投资建设有限公司,湖北 武汉 430060)
为研究混凝土斜拉桥在高速铁路上的适应性,以主跨260 m高速铁路双塔混凝土斜拉桥为例,根据功能需要和场地条件进行桥梁结构设计,然后通过建立空间三维有限元模型,综合采用最小弯曲能量法和影响矩阵法确定斜拉桥的合理成桥状态。在合理成桥状态下,斜拉索索力均匀,桥梁整体处于桥塔预偏、中跨预拱状态。最后,分析混凝土加劲梁的竖向、横向刚度以及桥塔变形,研究温度作用和混凝土收缩徐变效应对行车安全性和舒适性的影响,并对混凝土加劲梁、桥塔以及斜拉索的强度进行验算。分析结果表明,大跨度混凝土斜拉桥各受力构件的强度和刚度均满足高速铁路行车要求。
高速铁路;斜拉桥;混凝土梁;结构设计;受力性能;合理成桥状态;最小弯曲能量法;收缩徐变

混凝土斜拉桥将抗拉性能好的钢丝索和抗压性能好的混凝土有机地结合起来,充分发挥了2种材料的优点,具有造价低、刚度大、抗风稳定性好的特点[12]。混凝土斜拉桥已在国内外的公路桥梁中得到了广泛的应用。在国外,1991年建成的挪威斯卡恩圣特桥(Skamsundet Bridge)主跨达530 m,为世界最大跨度混凝土斜拉桥。在国内,我国自20世纪80年代以来,陆续建成了一大批大跨度公路混凝土斜拉桥,2002年建成的荆沙长江公路大桥主跨达到500 m,为世界第2大跨度的混凝土斜拉桥[3]。但是,混凝土斜拉桥在国内外铁路桥梁中的应用尚不多[4]。在国外,英国、日本、德国等国建有几座跨度为55~150 m的铁路混凝土斜拉桥,最大跨度的铁路混凝土斜拉桥为主跨330 m的巴拉那河公铁两用桥。在国内,1981年建成的广西来宾红水河铁路桥主跨96 m,为我国第一座铁路混凝土斜拉桥。邵长宇等[56]对主跨240~360 m的高速铁路混凝土斜拉桥进行了初步研究,但是这些方案未能实施。2014年,沪昆高铁的联络线上建成了主跨112 m的混凝土斜拉桥[7]。近年来,随着高强混凝土技术的发展、车桥耦合动力仿真分析技术的提高、大跨度铁路斜拉桥的技术以及预制节段拼装技术的进步,大跨度铁路混凝土斜拉桥因其良好的经济技术性能被提出并实施,如在建的乐清港铁路支线瓯江特大桥即为主跨300 m的铁路混凝土斜拉桥,而主跨300 m左右的钢混叠合梁斜拉桥也开始应用于高速铁路中[8],钢桁梁铁路斜拉桥技术日臻成熟[911],但是混凝土斜拉桥在高速铁路正线桥梁中尚无应用实例。本文以广汕高铁增江特大桥为例,开展高速铁路大跨度混凝土斜拉桥设计研究,以期实现混凝土斜拉桥在高速铁路正线上的应用突破。
1 工程概况
广汕高铁增江特大桥在增城市石滩镇葵湖村与塘头村之间跨越增江,桥址处江面宽约700 m,主河槽宽约240 m,水深约10 m,铁路线路法线方向与水流方向夹角为约45°。受站场高程、航道等条件限制,主桥采用(48+84+260+84+48) m混凝土斜拉桥,立面布置图见图1。线路标准为双线客运专线,线间距5.0 m,设计最高行车速度250 km/h,有砟轨道,主桥平面位于为直线上。

图1 广汕高铁增江特大桥主桥立面布置
2 高速铁路大跨度混凝土斜拉桥结构设计
2.1 结构总体设计与结构体系
(48+84+260+84+48) m双塔双索面混凝土斜拉桥加劲梁全长526 m,斜拉索关于索塔对称布置,全桥共60对斜拉索,其中,边跨斜拉索自索塔向梁端依次编号为S1~S15,中跨斜拉索自索塔向跨中依次编号为M1~M15。梁上最内侧索距离塔中心12 m,其余索的纵向间距为8 m,桥塔上拉索的竖向间距为2 m,最外侧索的水平夹角为30°,桥面以上塔高为73 m,结构总体设计立面布置见图2。桥塔采用液压爬模法施工,加劲梁采用挂篮悬臂浇筑法施工,每个混凝土梁节段长8 m,全桥共69个节段。
桥梁结构体系采用半漂浮体系,混凝土加劲梁在桥塔处采用纵向滑动支座,纵桥向采用黏滞阻尼器与主塔下横梁连接,横桥向采用横向抗风支座限位,加劲梁在边墩和辅助墩处采用竖向和横向限位支座,可纵向滑动。
2.2 混凝土加劲梁
斜拉桥加劲梁采用单箱三室等高度混凝土箱梁,采用C60高性能混凝土,箱梁除了在连接墩、辅助墩、桥塔处设横隔板外,在斜拉索锚固处设置厚度35 cm的横隔板。加劲梁全宽16.0 m,中心处梁高3.5 m;挡砟墙内侧宽9.4 m,斜拉索横向间距为13.3 m。混凝土加劲梁横截面构造见图3。
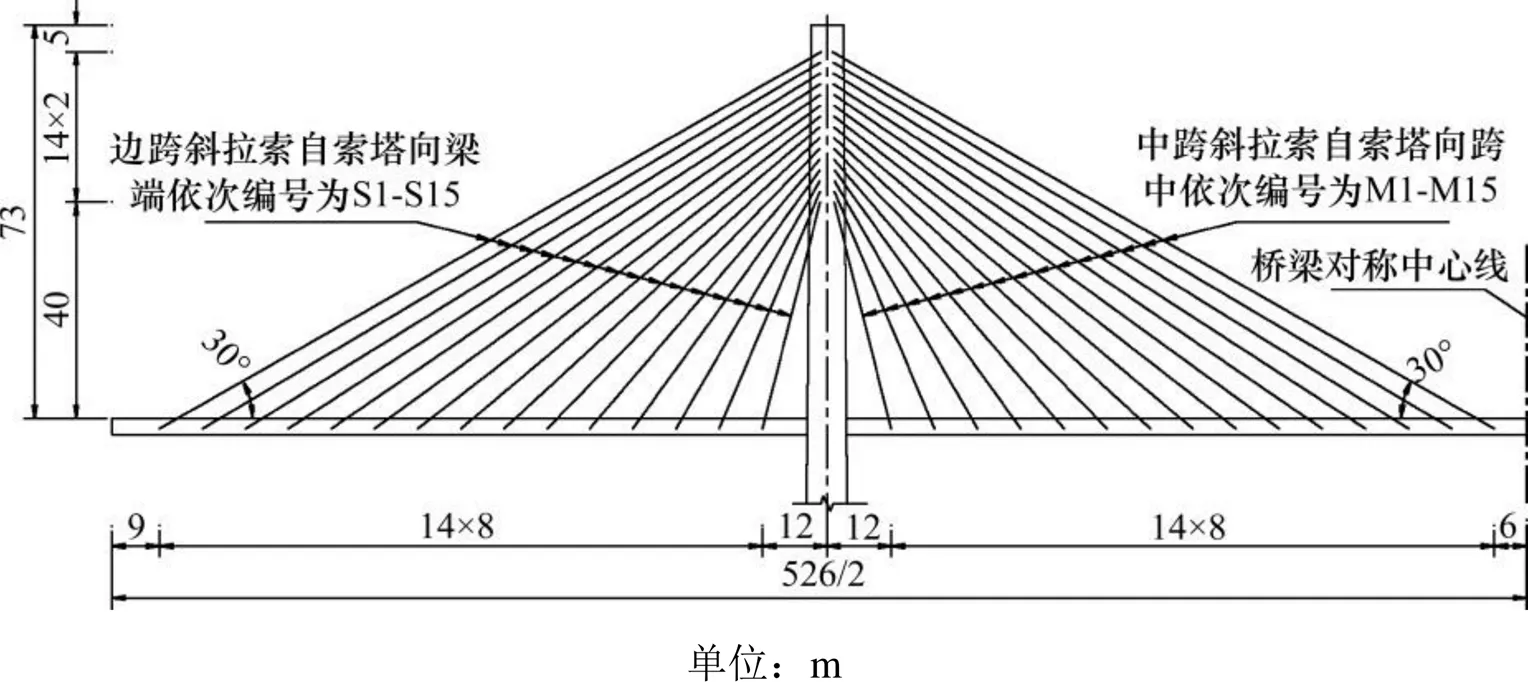
图2 主跨260 m混凝土斜拉桥结构总体布置

图3 混凝土加劲梁横截面
为了适当增加边跨梁体的重量,加劲梁边跨的顶底板和腹板的厚度由边跨向中跨逐渐减小,箱梁中间室的顶、底板厚由边跨的0.70 m渐变至中跨跨中的0.35 m,箱梁两边室的顶、底板厚由边跨的0.60 m渐变至中跨的0.35 m,箱梁的腹板厚由边跨0.60 m渐变至中跨的0.45 m。
纵向预应力筋布置:混凝土加劲梁顶、底板设纵向预应力钢索,采用规格为19-15.2 mm,27-15.2 mm的钢绞线。另设45-15.2 mm钢绞线的体外索。
横向预应力筋布置:在斜拉索吊点位置设置规格为5-15.2 mm,17-15.2 mm低松弛预应力钢绞线,单端交错张拉。
2.3 索塔及桥墩
采用花瓶形索塔,塔总高99 m,梁面以上塔高73 m,其中下塔柱高17.3 m,中塔柱高44.7 m,上塔柱高37 m,均采用矩形空心截面,上塔柱中心横桥向间距13.3 m。塔柱纵桥向宽由塔顶的6 m渐变至塔底的8 m,上塔柱和中塔柱截面横桥向宽4.5 m,下塔柱横桥向宽由4.5 m增加至6 m,索塔正面、侧面布置见图4。塔柱采用单箱单室混凝土截面,采用C50混凝土,顺桥向的壁厚为1.0 m,横桥向的壁厚为1.5 m。
索塔设上下2道横梁,上横梁采用单箱单室钢筋混凝土截面,高×宽为3.0 m×4.5 m,壁厚0.5 m。下横梁采用单箱单室预应力混凝土截面,高×宽为0.45 m×0.55 m,顶底板厚0.8 m,两侧腹板厚1.0 m。下横梁对应支座处局部加高1.0 m,中间留3.5 m×2.0 m的空间用于检查小车的通过。下横梁布置预应力钢索,规格为19-15.2 mm钢绞线。
S1~S9,M1~M9斜拉索在上塔柱上采用预应力混凝土齿块锚固,S10~S15,M10~M15斜拉索在上塔柱上采用钢锚箱锚固,拉索编号详见图2。
连接墩及辅助墩采用矩形截面实体墩;在辅助墩墩顶中间留3.5 m×2.0 m的空间用于检查小车的通过。
2.4 斜拉索
斜拉索采用公称直径7 mm的Ⅱ级松弛镀锌平行钢丝,抗拉标准强度1 960 MPa,成品拉索弹性模量=2.0×105MPa,技术指标符合《斜拉桥热挤聚乙烯高强钢丝拉索技术条件》(GB/T18365—2018)的要求。全桥共设60对斜拉索,按双索面扇形布置,其中PES(C)7-199型斜拉索20对、PES(C)7-253型斜拉索16对、PES(C)7-301型斜拉索24对,配套使用冷铸镦头锚,最大斜拉索长为141.80 m。

图4 索塔正面、侧面布置
3 高速铁路大跨度混凝土斜拉桥结构计算分析
3.1 有限元计算分析模型
采用MIDAS Civil建立空间有限元模型,加劲梁、桥塔、桥墩采用空间梁单元模拟,斜拉索采用空间索单元模拟,索与梁及索与塔之间采用刚性连接,考虑了斜拉索几何非线性的影响,按恩斯特公式计算斜拉索的换算弹性模量,采用弹簧刚度矩阵模拟桩基的桩土相互作用。有限元分析模型见图5。
3.2 确定斜拉桥合理成桥状态
斜拉桥是一种高次超静定结构,当它的结构体系确定之后,可以通过调整斜拉索索力使得斜拉桥的内力与线形达到最合理的状态,确定斜拉桥合理成桥状态的关键是优化斜拉桥的成桥索力[1214]。斜拉桥成桥索力优化方法主要有指定结构状态优化法、最小弯曲能量(弯矩)法、数学优化法、影响矩阵法、分步优化法等[1516]。
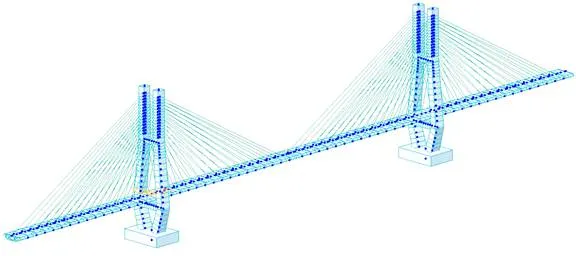
图5 有限元分析模型
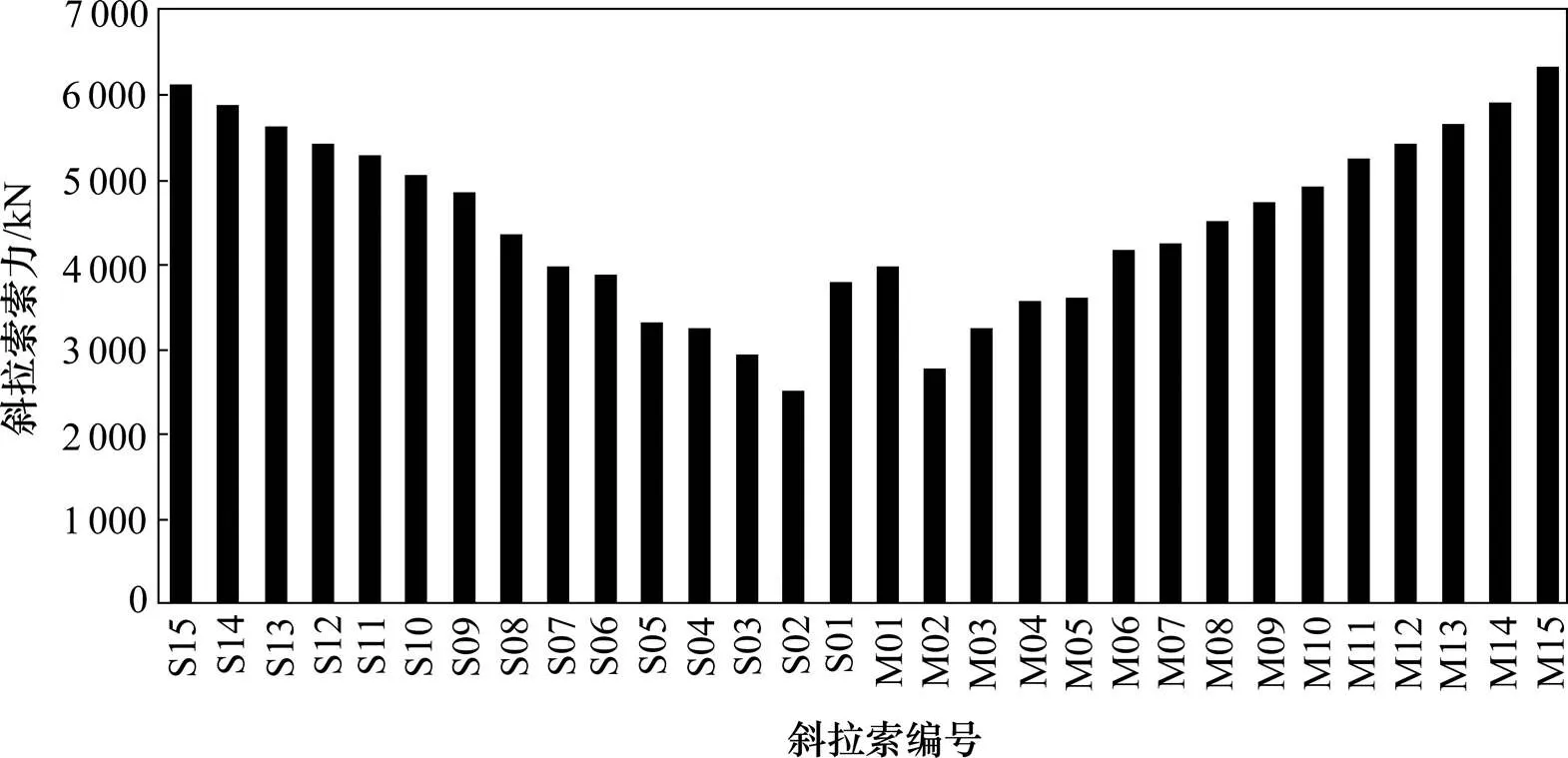
图6 斜拉桥成桥状态索力
本桥的合理成桥状态综合采用最小弯曲能量法和影响矩阵法确定,具体的计算分析步骤为: 1)用最小弯曲能量法初定成桥状态;2) 用影响矩阵法进行索力优化;3) 考虑几何非线性、收缩徐变等的影响微调索力。确定本桥合理成桥状态时的调整目标为:1) 索力分布较均匀,桥塔承受较小的不平衡弯矩,加劲梁弯矩呈锯齿状[17];2) 加劲梁变形为光滑的凸曲线或凹曲线,并且曲线斜率变化平缓[12];3) 成桥状态下桥塔顶向边跨侧有一定的预偏。采用上述方法优化后的斜拉桥成桥索力见图6,其中,边跨范围S15斜拉索索力最大,为6 129 kN,中跨范围M15斜拉索索力最大,为6 346 kN。
成桥状态加劲梁处于全截面受压状态,上缘最大压应力为12.5 MPa,最小压应力为1.8 MPa;下缘最大压应力为11.4 MPa,最小压应力为1.7 MPa。成桥状态加劲梁正应力分布见图7。
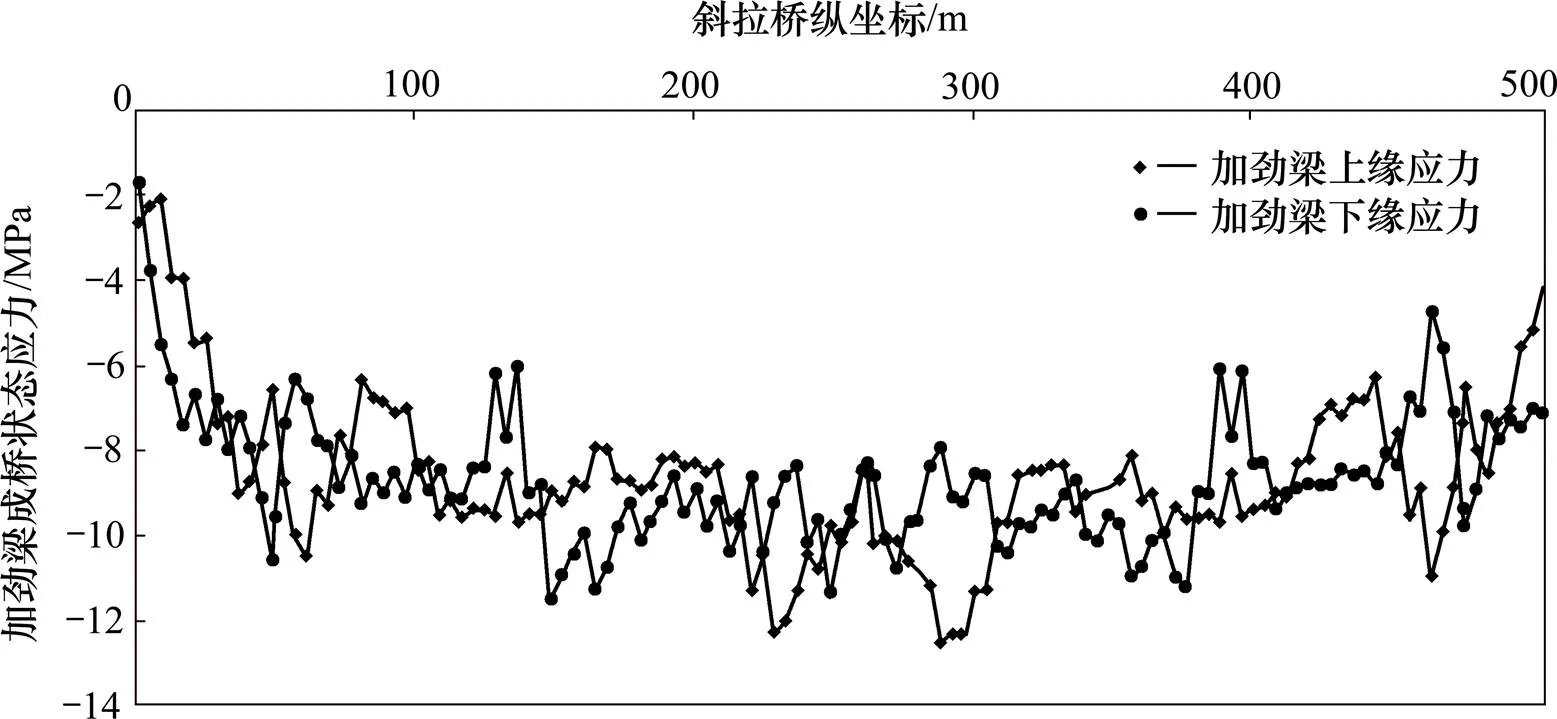
图7 成桥状态加劲梁应力
成桥状态加劲梁竖向变形呈现匀顺的波浪形曲线,第1跨(48 m跨)上拱6 mm,第2跨(84 m跨)下挠14.9 mm,主跨(260 m跨)上拱70.7 mm,加劲梁竖向位移图见图8。成桥状态下,主塔向边跨侧纵向位移33.7 mm(见图9),为活载作用预留了一定的预偏量。
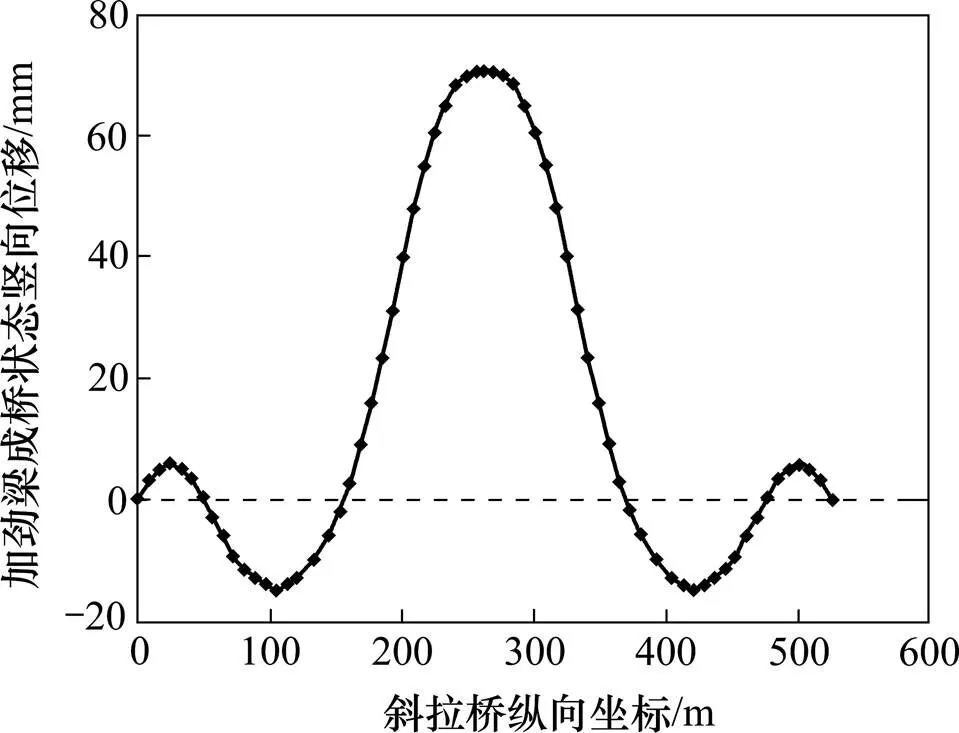
图8 成桥状态加劲梁竖向位移
3.3 斜拉桥刚度分析研究
3.3.1 加劲梁竖向刚度分析
混凝土加劲梁在活载及温度作用下主跨跨中变形分析结果见表1。在列车竖向静活载作用下,混凝土加劲梁主跨跨中最大竖向挠度为−213.9 mm,挠跨比1/1 216<1/1 000,梁端最大转角0.54‰< 1.0‰。在ZK静活载与温度变化的组合作用下,混凝土加劲梁主跨跨中最大竖向挠度为−241.9 mm,挠跨比为1/1 075<1/1 000,梁端最大转角0.93‰< 1.0‰。因此混凝土加劲梁在活载及温度变形组合作用下的挠度及梁端转角满足规范要求。
近年来的理论研究及桥梁健康监测结果表明,混凝土斜拉桥的收缩徐变变形一般在成桥后3 a内完成55%~65%,在成桥后10 a收缩徐变变形基本趋于稳定[1819]。本桥在铺轨3 a和10 a后加劲梁竖向变形计算结果见图10,从图中可以看出,铺轨3 a后和10 a后混凝土收缩徐变引起的中跨跨中竖向位移分别为44.1 mm和78.2 mm。对于大跨度斜拉桥可按/5 000控制收缩徐变变形,因此本桥的收缩徐变下挠值不宜大于52 mm,铺轨3 a后中跨收缩徐变下挠44.1 mm<52 mm,在之后的运营期间中跨收缩徐变下挠值将超过52 mm。在实际建设和运营中,一方面可在通车后进行加劲梁竖向变形监测,并在铺轨3 a后进行一次索力和线形调整,恢复初始铺轨时的桥面线形;另一方面可在施工阶段设置一定预拱度(预拱约20 mm)来减小收缩徐变的影响。
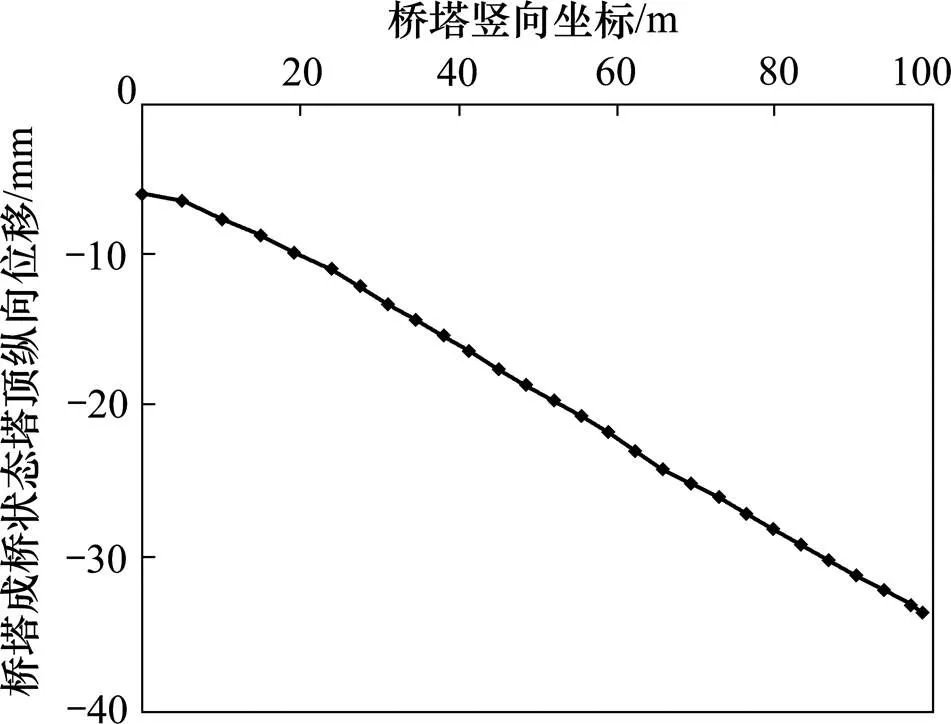
图9 成桥状态桥塔塔顶纵向位移

表1 混凝土加劲梁在活载及温度作用下主跨跨中变形
为了研究混凝土收缩徐变变形对高速列车过桥时的影响,将温度作用及收缩徐变(铺轨后10 a)效应引起的加劲梁竖向变形作为初始不平顺叠加至轨面不平顺谱中进行了车桥耦合动力仿真分析。分析结果表明,时速250 km高速旅客列车过桥时,斯佩林舒适度指标达到“良”以上,脱轨系数及轮重减载率均满足规范要求。因此,即使混凝土收缩徐变使中跨下挠78.2 mm,列车过桥的安全性和舒适性仍然是有保障的。

图10 铺轨后加劲梁竖向收缩徐变变形
3.3.2 加劲梁横向刚度分析
在列车横向摇摆力、横向风力及温度组合作用下,混凝土加劲梁主跨跨中最大水平位移为3.4 mm,挠跨比为1/72 222</4 000,满足规范要求。
3.3.3 桥塔变形分析
在双线ZK活载作用下,塔顶最大纵向位移为86.4 mm(向跨中),扣减成桥状态下塔顶向边跨侧的预偏量33.7 mm,塔顶在活载作用下的实际最大纵向位移为52.7 mm(向跨中),塔顶纵向位移在合理范围内。
3.4 斜拉桥强度验算
3.4.1 混凝土加劲梁强度验算
加劲梁采用C60高性能混凝土。主力工况下,加劲梁处于全截面受压状态,最大压应力15.7 MPa<20 MPa,最小压应力1.1 MPa;主力+附加力工况下,加劲梁仍处于全截面受压状态,最大压应力17.3 MPa<26 MPa,最小压应力0.8 MPa。混凝土加劲梁强度满足规范要求。
3.4.2 斜拉索强度及疲劳性能验算
斜拉索采用抗拉标准强度1 960 MPa的平行钢丝索。主力工况下,斜拉索最大拉应力为645 MPa,拉索最小安全系数3.04;主力+附加力工况下,斜拉索最大拉应力为651 MPa,拉索最小安全系数3.01。因此,斜拉索安全系数均大于2.5,满足规范要求。列车活载作用下斜拉索最大应力幅为112.6 MPa(出现在边跨斜拉索S11上,见图11)<200 MPa,斜拉索疲劳应力幅满足规范要求。
3.4.3 桥塔强度验算
桥塔采用C50混凝土。主力工况下,桥塔处于全截面受压状态,最大压应力14.2 MPa<16.8 MPa;主力+附加力作用下,桥塔仍处于全截面受压状态,最大压应力17.8 MPa<21.8 MPa。混凝土桥塔的强度满足规范要求。

图11 斜拉索最大应力幅
4 结论
1) 时速250 km高速铁路混凝土斜拉桥主跨260 m,边跨设1个辅助墩后跨径组成为(48+84) m,采用双塔双索面结构形式、半漂浮结构体系,桥塔为花瓶型,桥面以上塔高73 m,加劲梁采用单箱三室箱形截面,梁高3.5 m,宽16 m,标准梁段斜拉索间距为8 m。
2) 混凝土斜拉桥受到的活载与恒载之比为0.163,边跨与中跨之比为0.507,桥面以上塔高与中跨之比为0.28,拉索最小倾角为30°,梁高与跨径之比为0.013,梁宽与梁高之比为4.57,上述参数与公路斜拉桥的参数取值存在较大区别,体现了铁路混凝土斜拉桥刚度大、承载能力强的特点。
3) 通过建立空间三维有限元模型,综合采用最小弯曲能量法和影响矩阵法确定斜拉桥的合理成桥状态,在合理成桥状态下铁路混凝土斜拉桥处于“梁预拱塔预偏”状态,斜拉索索力均匀,桥塔塔顶向边跨侧预偏33.7 mm,中跨上拱70.7 mm,混凝土加劲梁处于全截面受压状态,最小压应力 1.7 MPa。
4) 在确定合理成桥状态的基础上,分析混凝土加劲梁的竖向、横向刚度以及桥塔变形,研究温度作用和混凝土收缩徐变效应对行车安全性和舒适性的影响,并对混凝土加劲梁、桥塔以及斜拉索的强度进行验算,并分析斜拉索的疲劳性能。分析结果表明,本桥各受力构件的强度和刚度均满足高速行车要求。
[1] TANG Manchung, 陈守容. 混凝土斜拉桥[J]. 世界桥梁, 1989(1): 52−63. TANG Manchung, CHEN Shourong. Concrete cable-stayed bridge[J]. World Bridge, 1989(1): 52−63.
[2] 何智. 混凝土斜拉桥索力优化研究[D].成都: 西南交通大学, 2011: 6−7. HE Zhi. Research on cable force optimization of concrete cable-stayed bridge[D]. Chengdu: Southwest Jiaotong University, 2011: 6−7.
[3] 姚康宁. 大跨度混凝土斜拉桥运营阶段混凝土收缩徐变影响研究[D]. 长沙: 长沙理工大学, 2006: 1−4. YAO Kangning. Study on the effect of concrete shrinkage and creep in operation stage of long-span concrete cable-stayed bridge[D]. Changsha: Changsha University of Science and Technology, 2006: 1−4.
[4] 王新忠, 周水兴, 李峰辉. 混凝土斜拉桥发展与展望[J]. 中国市政工程, 2006(2): 22−24, 91. WANG Xinzhong, ZHOU Shuixing, LI Fenghui. Development and prospect of concrete cable-stayed bridges[J]. China Municipal Engineering, 2006(2): 22− 24, 91.
[5] 邵长宇. 新世纪中国铁路斜拉桥发展展望[C]// 中国土木工程学会桥梁及结构工程学会年会. 南京, 2000: 54−60.SHAO Changyu. Prospects for the development of China railway cable-stayed bridge in the new century[C]// Annual Meeting of the Society of Bridges and Structural Engineering of China Civil Engineering Society. Nanjing, 2000: 54−60.
[6] 高芒芒, 潘家英, 程庆国. 高速铁路预应力混凝土斜拉桥动力特性研究[C]// 中国土木工程学会桥梁及结构工程学会第十三届年会论文集(上册). 上海, 1998: 41− 48. GAO Mangmang, PAN Jiaying, CHENG Qingguo. Study on dynamic characteristics of high-speed railway prestressed concrete cable-stayed bridge[C]// Proceedings of the 13th Annual Meeting of the Society of Bridges and Structural Engineering of China Civil Engineering Society (Volume 1). Shanghai, 1998: 41−48.
[7] 闫斌, 戴竞尧. 高速列车与跨线斜拉桥耦合气动效应研究[J]. 铁道科学与工程学报, 2013, 10(5): 18−22. YAN Bin, DAI Jingyao. Aerodynamic effect of high-speed train on overpass cable-stayed bridge[J]. Journal of Railway Science and Engineering, 2013, 10(5): 18−22.
[8] 王德志, 杨恒, 曾甲华, 等. 福州至厦门高速铁路桥梁总体设计[J]. 铁道标准设计, 2019, 63(8): 67−73. WANG Dezhi, YANG Heng, ZENG Jiahua, et al. General design of Fuzhou-Xiamen high-speed railway bridges[J]. Railway Standard Design, 2019, 63(8): 67−73.
[9] GUO H, LIU X, ZHAO X. Parametric study on Hutong highway and railway bridge[C]// 19th IABSE Congress. Stockholm, 2016: 1−8.
[10] HE X, WU T, ZOU Y, et al. Recent developments of high-speed railway bridges in China[J]. Structure and Infrastructure Engineering, 2017,13(12): 1−12.
[11] HE X, QIN H, LIU W, et al. Design, analysis and construction of a steel truss cable-stayed bridge for high-speed railway in China[J]. Structural Engineering International, 2016, 26(4): 381−388.
[12] 苏剑南. 厦漳跨海大桥北汊主桥合理成桥状态研究[J].桥梁建设, 2013, 43(4): 44−48. SU Jiannan. Study of rational completed bridge state of north main bridge of Xiazhang sea-crossing bridge[J]. Bridge Construction, 2013, 43(4): 44−48.
[13] 武利军. 基于Midas的斜拉桥索力优化方法与工程实例[J]. 公路与汽运, 2012(5): 163−166. WU Lijun. Cable force optimization method and engineering example of cable-stayed bridge based on Midas[J]. Highways & Automotive Applications, 2012(5): 163−166.
[14] 李熠. PC斜拉桥合理成桥状态研究[D]. 长沙: 长沙理工大学, 2009. LI Yi. Research on reasonable finished state of PC cable-stayed bridges[D]. Changsha: Changsha University of Science and Technology, 2009.
[15] 戴杰, 秦凤江, 狄谨, 等. 斜拉桥成桥索力优化方法研究综述[J]. 中国公路学报, 2019, 32(5): 17−37. DAI Jie, QIN Fengjiang, DI Jin et al. Review on cable force optimization methods for cable-stayed bridge in completed bridge state[J]. China Journal of Highway and Transport, 2019, 32(5): 17−37.
[16] 田源, 杨海霞. 斜拉桥成桥索力优化理论及方法的最新进展[J]. 三峡大学学报(自然科学版), 2013, 35(2): 47−52. TIAN Yuan, YANG Haixia. Recent developments of optimization theory and methods for bridge-completing cable force of cable stayed bridge[J]. Journal of China Three Gorges University (Natural Sciences), 2013, 35(2): 47−52.
[17] 颜东煌, 李学文, 刘光栋, 等. 混凝土斜拉桥合理成桥状态确定的分步算法[J]. 中国公路学报, 2003(1): 44−47. YAN Donghuang, LI Xuewen, LIU Guangdong, et al. Step-by-step arithmetic for the reasonable finished dead state of the concrete cable-stayed bridges[J]. China Journal of Highway and Transport, 2003(1): 44−47.
[18] 蔺彦堃. 混凝土时变效应对斜拉桥变形的影响分析[J].青海交通科技, 2017(4): 86−88. LIN Yankun. Influence of time-dependent effect of concrete on deformation of cable-stayed bridge[J]. Qinghai Transportation Science & Technology, 2017(4): 86−88.
[19] 于景飞, 吴炎奎, 苏醒. 大跨径混凝土斜拉桥线形优化预测研究[J]. 铁道科学与工程学报, 2018, 15(1): 133− 140. YU Jingfei, WU Yankui, SU Xing. Study on prediction of line optimization of large-span concrete cable-stayed bridges[J]. Journal of Railway Science and Engineering, 2018, 15(1): 133−140.
Design and research of long-span concrete cable-stayed bridge for high-speed railway
GONG Junhu1, 2
(1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Maglev Tansportaion Investment and Construction Co. Ltd, Wuhan 430060, China)
The concrete cable-stayed bridge has the characteristics of low cost, high rigidity and good wind resistance stability. It has been widely used in highway bridges, but it is rarely used in railway bridges, especially in high-speed railway trunk bridges. Therefore, it is necessary to carry out in-depth research on the adaptability of concrete cable-stayed bridges on high-speed railways. Taking the double-tower concrete cable-stayed bridge with a main span of 260m for high-speed railway as an example, the bridge structure design was carried out according to the functional needs and site conditions. Then, by establishing the spatial three-dimensional finite element model, the reasonable finished dead state of the cable-stayed bridge was determined by the minimum bending energy method and the influence matrix method. In which state, the cable tensions were uniform, and the bridge was in the pylon pre-bias state and the mid-span pre-arch state as a whole. Finally, the vertical and lateral stiffness of the concrete stiffening beam and the deformation of the pylon were analyzed, and the effects of temperature and concrete shrinkage and creep on the safety and comfort of the vehicle were studied. The strength of concrete stiffening beams, pylons and stay cables was also checked. The analysis results show that the strength and stiffness
high-speed railway; cable-stayed bridge; concrete beam; structural design; force performance; reasonable finished dead state; minimum bending energy method; shrinkage and creep of the members of the long-span concrete cable-stayed bridge meet the requirements of high-speed railway driving.
10.19713/j.cnki.43−1423/u.T20190971
U448.13;U448.27;U24
A
1672 − 7029(2020)07 − 1611 − 09
2019−11−04
浙江省交通运输厅科研计划资助项目(2017002)
龚俊虎(1983−),男,湖北天门人,高级工程师,博士研究生,从事大跨度桥梁及磁浮交通桥梁设计与研究;E−mail:598559852@qq.com
(编辑 阳丽霞)
