热备动车组配置方案优化模型
2020-08-07徐禾颖彭小倩倪少权杨晓军张杰
徐禾颖,彭小倩,倪少权,杨晓军,张杰
热备动车组配置方案优化模型
徐禾颖1, 2, 3,彭小倩1, 2, 3,倪少权1, 2, 3,杨晓军4,张杰1, 2, 3
(1. 西南交通大学 交通运输与物流学院,四川 成都 610031;2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031;3. 综合交通大数据应用技术国家工程实验室,四川 成都 610031;4. 中国铁路西安局集团有限公司 西安北站,陕西 西安 710016)
热备动车组的配置方案影响热备动车组的救援效率,对保证铁路正常运行秩序起着重要作用。针对配置方案中热备动车组数量的确定和备用地点的选择,以全面覆盖铁路事故风险为约束,分别以热备动车组平均响应时间最短及配置成本最少为目标,建立热备动车组配置方案优化的多目标规划模型,并设计分步搜索的禁忌搜索算法对多目标模型的Pareto解集进行求解,最后结合算例,验证了模型和算法的可靠性。研究结果表明,得到的热备动车组配置方案能够满足决策制定者的不同偏好,热备动车组配置数量和地点协同优化的方案较两者分步优化更能提高热备动车组应急效率。
热备动车组;配置方案;多目标规划;禁忌搜索;Pareto解集

热备动车组是指检修完毕、技术状态良好、作为应急备用、随时可以上线使用的动车组,当线路上运行的动车组由于恶劣天气、线路基础设施或动车组故障等原因出现中途停止运行或晚点时,往往可以通过启动热备动车组用于车底交路受影响时担当后续交路、动车组故障时接运旅客及救援动车组。热备动车组对于保证正常的运营秩序起着至关重要的作用,为了提高热备动车组的应急效率,有必要对热备动车组的配置方案进行研究。热备动车组的配置方案是根据动车组配属和运用的实际情况,确定热备动车组的存放地点、车型和数量的方案[1]。目前国内外专门针对热备动车组的研究较少,主要为了优化动车组的运用计划而对热备动车组有所涉及[1−4]。针对配置方案的研究有基于层次分析法的选址评价模型[5]、0-1规划模型[6],但还存在缺少对路网复杂条件的考虑、未能对热备动车组配置方案进行整体优化等不足。由于热备动车组配置方案的研究与应急资源选址模型类似,因此相关研究有一定的借鉴意义。选址模型中较为成熟的模型有中值模型和覆盖模型等。中值模型旨在优化资源点到待救援点的响应时间,最早由Hakimi[7]提出,在这此基础上有学者将这一理论应用于救援车选址[8−9],我国学者也利用这一理论进行交通网救援设施的选址,并引入时间价值[10]、理想灰关联[11]、网络脆弱性分析[12]等理论。覆盖模型旨在优化救援车的配置地点实现对待救援点的覆盖,Church等[13]在1974年提出最大覆盖模型,并进一步衍生出集合覆盖模型和最大覆盖模型2个主要分支。从覆盖的对象来区分,可分为点覆盖模型和弧段覆盖模型,在对交通运输网覆盖选址模型的研究中,学者们多从复杂路网中抽象出待救援的节点,建立点覆盖模型对救援资源的布局进行优化[14−17]。当热备动车组到始发车站担当后续交路时,点覆盖模型具有一定的借鉴意义,然而当热备动车组接运旅客及救援动车组时,由于突发事件发生的地点具有不确定性,仅使用点覆盖模型可能具有一定的局限性,故可以考虑引入弧段覆盖模型。最大弧段覆盖模型由Revelle等[18]提出;Church等[19]提出最大弧覆盖的混合整数规划模型;Berman等[20]进一步引入弧段覆盖比例的概念,WANG等[21]针对Berman的模型设计了领域搜索算法提高了运算速度,Blanquero等[22]从待选点连续分布的角度对弧段覆盖理论进行了扩充;舒周攀[23]在弧段覆盖模型的基础上提出了多重覆盖模型;汤霖等[24]利用最大覆盖模型解决铁路救援列车部署问题。可以看出,目前针对热备动车组配置方案的研究较少,主要研究热备动车组的管理模式和备用地点选择。但热备动车组配置方案中的3部分内容不是相互独立的,合理的热备动车组配置方案应是对热备动车组备用数量、备用车型和热备地点的综合优化[5];这其中,配置数量和热备地点的合理匹配对热备动车组的使用效率有较大影响,当两者匹配时,动车组的利用率最高[25]。其次,由热备动车组的出动条件可以看出,热备动车组的配置既要满足去始发车站担当后续交路的需求,又要满足覆盖铁路事故风险的需求,单纯的点覆盖模型和弧段覆盖模型都有不相适应的地方。最后,由于热备动车组的配置相对灵活,在配置方案中可能存在多列热备动车组配置在同一车站的情况,与传统的选址模型有所不同。因此本文针对热备动车组配置方案的优化问题,以全面覆盖铁路事故风险为前提,提出热备动车组配置的2个目标:平均响应时间最短和配置成本最低;并基于这2个目标建立多目标规划模型,研究热备动车组的配置数量和配置地点;设计禁忌搜索算法对模型进行求解;最后进行算例分析。
1 热备动车组配置模型的建立
综合分析铁路救援的特点及热备动车组的作用,热备动车组配置方案应当能够全面覆盖铁路事故风险,便于热备动车组准备和快速响应。在确定热备动车组的车型时,由于热备动车组需要替代下线动车组承担其的运输任务,还需要救援动车组,因此热备动车组的车型在列车定员、速度等级等方面应当能够兼容目前上线运行的运用车,并具有救援动车组的能力,故热备动车组车型的确定应当根据各铁路局实际情况来确定。本文主要针对热备动车组备用数量的确定和备用地点的选择,建立热备动车组配置方案优化模型。
1.1 模型假设
1) 热备动车组备选节点对自身的救援时间为热备动车组出动准备时间;
2) 热备动车组热备在各备选点的准备时间相同,均为10 min;
3) 模型中涉及到的区间运行时分仅指从热备地点到救援地点之间的时间,不考虑热备动车组在存放节点内的走行时间;
4) 热备动车组列车收到出动指令后始终以安全允许最大速度赶到救援地点;
5) 突发事件发生后,每个热备动车组需求点仅由1列热备动车组提供服务;
6) 将待研究的高速铁路线路网抽象为有向网络图(,),表示路网中的节点集合,表示路网中的弧段集合,弧段数量为N。表示在路网中具有部署热备动车组条件的节点集合,节点个数为N,为待选点索引,∈;表示路网中有始发列车的车站的集合,数量为N,热备动车组可能需要去到这些车站担当后续交路,为始发车站索引,∈;表示弧段,∈,热备动车组在这些弧段上可能需要接运旅客或救援动车组。
1.2 热备动车组配置模型
1.2.1 目标函数
1) 热备动车组救援平均响应时间最短
当热备动车组担当后续交路时,热备动车组到达各始发车站的加权时间T为:

各始发车站的权重由车站连接各方向的终到列车发生晚点的概率确定:

各始发车站的权重为:
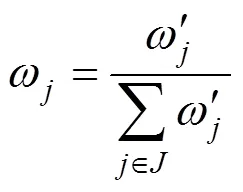
当热备动车组出动接运旅客或救援动车组时,热备动车组到达路网中各弧段的加权时间T为:

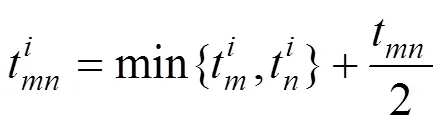
弧段的权重由弧段内发生需要出动热备动车组的事故的概率与发生事故带来的损失确定,具体为:

各弧段的权重为:

故热备动车救援的平均响应时间最短这一目标可表示为:


2) 热备动车组配置成本最低
考虑到热备动车组的购置成本和日常维护的成本,从提高热备动车组的利用率、避免资源浪费的角度,在制定方案时应当尽可能以最少的热备动车组数量实现对路网中风险的全面覆盖,同时降低热备动车组日常维护成本,故建立成本目标:

式中:表示1列热备动车组的购置成本,以折旧的方式计入热备动车组日常维护成本;c表示1列热备动车组热备在节点所需的日常维护成本。
1.2.2 约束条件
1) 突发事件发生后,每个热备动车组需求点仅由1列热备动车组提供服务;对"∈,"∈:
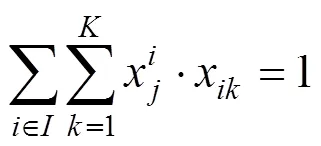


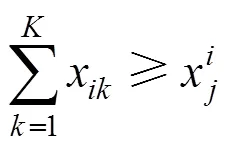

3) 每台热备动车组均有且只能有1个热备地点;对"=1,2,…,:
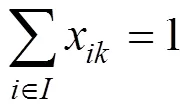



5) 使发生需要热备动车组时却无热备动车组可用的事件的概率低于合理预期值。铁路局内热备动车组需求点的个数为始发车站数量N及弧段数量N之和,第个需求点发生必须出动热备动车组的事故的概率为q,假定每个需求点是否发生必须出动热备动车组的事件是相互独立的,可得到有个需求点同时需要热备动车组的概率P为:

式中:r表示当需求点数量为时,第种组合方式下热备动车组的需求点集合。

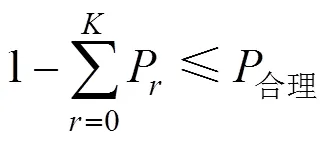


2 热备动车组配置模型的求解
由于热备动车组配置模型具有组合优化和多目标的特性,因此算法的设计以获得模型的Pareto解集为目的。为求解该问题,本文提出分步搜索的禁忌搜索算法。
首先给出Pareto解集的求解算法:
Step 1:给定有个候选解的解集,i=1,Pareto解集={1},j=1;转Step 2;
Step 2:若i>,输出Pareto解集;否则转Step 3;
Step 4:j=j+1;若j≤length(),转Step 3;否则转Step 5;
在采用禁忌搜索算法时,需要对算法的参数进行设定:
1) 解的组成

2) 初始解的产生
由于初始解的选择会对算法的执行效率产生影响,因此通过随机产生一组解,取其有效解集作为模型的初始解。
3) 邻域的构建
4) 评价函数
模型的评价函数为模型的2个目标函数。
5) 禁忌表和禁忌长度
选取禁忌对象为每次迭代中评价值最小的解,禁忌长度取静态值。
6) 特赦及停止准则
特赦准则采取“best so far”准则,停止准则采取最大迭代次数N。
禁忌算法的求解过程如下:

Step 3:判断当前值是否满足式(18),若不满足,转Step 10;若满足,转Step 4;
Step 4:产生初始解集,Pareto解集置为初始解集;转Step 5;
Step 6:产生当前解的领域,依据Pareto解集求解算法更新解集,并判断加入的解是否在禁忌表中,若不在,则将这些解放入禁忌表,转Step 7;
Step 7:计算禁忌表中节点频率;如果节点频率大于给定阈值,给当前最优解乘以惩罚系数,使得其被其他解支配,引导搜索跳出局部最优,转Step 8;
Step 9:重复Step 4至Step 8直到满足本次循环终止条件,转Step 10;
3 算例分析
3.1 算例描述
以某铁路局高速铁路为例,该铁路局管内高速铁路网示意图如图1所示。
热备动车组备用地点选择在有存车条件的车站和动车段,本例中为3,5,6,7,8,20,22,23,24,25,26,29和3013个备选节点。在各备选节点配置1列热备动车组,每年的日常维护开支(万元)分别为:1 650,1 215,1 215,1 416,1 554,1 790,1 440,1 470,1 610,1 948,2 270,1 720和1 910。
热备动车组的购置费用以净值为0的平均年限法进行折旧,1列热备动车组每年的购置成本取=400万元。
铁路局管内共7个始发车站:2,5,6,13,18,24和37,依据式(2)和式(3),各始发车站的权重分别为:0.04,0.36,0.38,0.07,0.11,0.02和0.03。
路局内共36个区间,依据热备动车组出动记录及各区间内发生事故的危险性评价结果,确定节点1和2之间的区间权重为0.076 83,节点8和9和9和10之间区间的权重为0.121 32,其余区间权重为0.020 62。热备动车组担当后续交路时合理接续时间1取3 h,热备动车组救援区间时合理救援时间2取2.5 h。依据热备动车组出动记录,确定1为0.5,2为0.5。
3.2 结果分析
采用MATLAB编程实现算法进行求解,按照初始解构造规则,通过随机产生50个解,取其有效解集作为初始解,邻域的构建取n=/2 (向上取整),最大迭代次数N=10,禁忌长度=5。得到该铁路局只需1列热备动车组即可实现对铁路局内事故风险的全面覆盖。优化结果中包含35个Pareto解,按照1降序、2升序的方式排列,如表1所示。
Pareto解集中的解即为多目标优化问题的最优解集,它展现了目标之间的博弈关系,提供了丰富的决策支持信息,能够满足不同决策制定者的不同偏好。

图1 某铁路局管内高速铁路网示意图

表1 模型Pareto解的各目标值及方案
从运算结果可以看出,当热备动车组列数较少时,增加列数可以较为明显地缩短热备动车组的响应时间,但从整体结果来看,增加热备动车组列数所能带来的响应时间节省十分有限,且会使配置成本激增。热备动车组的数量超过10列后,再增加热备动车组的数量将不会带来响应时间的减少。
为了说明热备动车组配置数量和热备地点协同优化的方案相较分别求解更具有优越性,将模型的有效解集和热备动车组数量给定情况下的最小响应时间进行方案对比,如图2所示。图2中“o”代表多目标模型的Pareto解的目标函数值,“+”代表不同热备动车组数量下响应时间最小的方案的目标函数值。
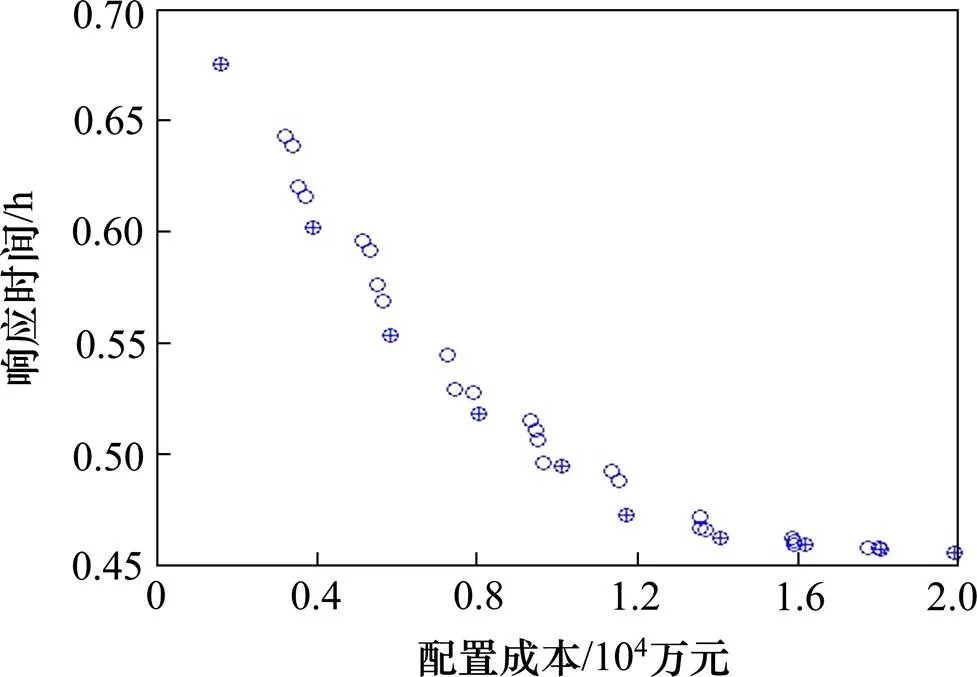
图2 方案对比
从图2中可以看出,多目标规划求得的解集不仅可以给出不同热备动车组数量下响应方案最优解,还可以给出更加丰富的决策信息,且方案中能够实现热备动车组数量和配置地点的协同优化。当路局内的热备动车组列数发生变化,或最佳方案中节点的股道运用紧张时,无需从头制定热备动车组的配置方案,只需在Pareto解集中依据需要重新选择即可。
4 结论
1)对热备动车组的配置方案进行研究,建立热备动车组配置列数和热备地点协同优化的热备动车组配置优化多目标规划模型,并设计模型求解的分步求解算法。从算例分析中可看出,本文提出的模型和算法可以有效地解决热备动车组配置问题,并能从平均响应时间和配置成本的角度给出相对较优的方案。
2) 在下一步的研究中,对始发车站和待救援弧段的权重还有优化的空间,可以针对不同的线路条件及不同车型的故障率分别进行讨论。
3) 除了综合考虑路局内的线路条件、热备动车组配置成本外,还可以进一步考虑乘务人员工作环境、车站的股道使用情况等相关因素,最终确定热备动车组的备用方案。
4) 下一步的研究中,可根据线上运行的动车组车型及动车组之间相互救援的条件,对热备动车组车型、数量和配置地点进行协同优化。
[1] 张芳英. 关于高速铁路启用热备动车组相关问题的探讨[J]. 甘肃科技, 2017, 33(17): 60−62. ZHANG Fangying. Discussion on relevant problems of starting up hot standby EMU[J]. Gansu Science and Technology, 2017, 33(17): 60−62.
[2] 李华. 高速铁路动车组运用计划编制理论与方法研究[D]. 北京: 北京交通大学, 2013. LI Hua. Theory and method studies on EMU scheduling problem for high speed railway[D]. Beijing: Beijing Jiaotong University, 2013.
[3] 周宇. 高速铁路成网条件下动车组运用计划编制理论与算法研究[D]. 北京: 北京交通大学, 2017. ZHOU Yu. Theory and algorithm research on train-set utilization problem under high speed railway network[D]. Beijing: Beijing Jiaotong University, 2017.
[4] 花伟, 张才春, 范振平, 等. 动车组动态备用方式研究[J]. 铁道运输与经济, 2011, 33(1): 27−30. HUA Wei, ZHANG Caichun, FAN Zhenping, et al. Study on dynamic standby mode of EMU[J]. Railway Transport and Economy, 2011, 33(1): 27−30.
[5] 孙宝策. 高速铁路动车组备用问题研究[D]. 北京: 北京交通大学, 2012. SUN Baoce. Research on spare EMU of high-speed railway[D]. Beijing: Beijing Jiaotong University, 2012.
[6] 郑康立,王正彬. 基于最大服务距离的动车组备用地点选择研究[J]. 铁道运输与经济, 2014, 36(5): 54−58. ZHENG Kangli, WANG Zhengbin. Study on spare location selection of EMU based on maximum service distance[J]. Railway Transport and Economy, 2014, 36(5): 54−58.
[7] Hakimi S L. Optimum locations of switching centers and the absolute centers and medians of a graph[J]. Operations Research, 1964, 12: 450−459.
[8] Calvo A, Marks H. Location of health care facilities: An analytical approach[J]. Socio-economic Planning Sciences, 1973, 7(5): 407−422.
[9] Carson Y, Batta R. Locating an ambulance on the Amherst Campus of the State University of New York at Buffalo[J]. Interfaces, 1990, 20(5): 43−49.
[10] 徐之恒. 地铁突发事件应急救援资源的配置研究[D]. 成都: 西南交通大学, 2012. XU Zhiheng. Research on the allocation of rescue resources for metro emergencies[D]. Chengdu: Southwest Jiaotong University, 2012.
[11] 卢媛媛, 郭志坚, 王宝玲, 等. 趋近理想灰关联多约束的交通救援中心中值选址模型[J]. 公路交通科技. 2018, 35(7): 114−119. LU Yuanyuan, GUO Zhijian, WANG Baoling, et al. A traffic rescue centre median location model approaching ideal grey relational constraints[J]. Journal of Highway and Transportation Research and Development, 2018, 35(7): 114−119.
[12] 冉连月, 吴贤国, 刘洋, 等. 武汉市轨道交通线网应急救援站选址研究[J]. 中国安全生产科学技术, 2018, 14(4): 63−68. RAN Lianyue, WU Xianguo, LIU Yang, et al. Study on site selection of emergency rescue stations in Wuhan rail transit network[J]. Journal of Safety Science and Technology, 2018, 14(4): 63−68.
[13] Church R L, Revelle C. The maximal covering location problem[J]. Papers of Regional Science Association, 1974(32): 101−118.
[14] 胡丹丹, 王国利, 杨超. 考虑服务数量和服务时间的紧急救援站选址[J]. 公路交通科技, 2012, 29(10): 133− 136. HU Dandan, WANG Guoli, YANG Chao. Location of emergency rescue station considering service quantity and time[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 133−136.
[15] 吴艳华, 王富章, 李芳. 铁路救援基地层级规划选址模型[J]. 交通运输工程学报, 2013, 13(3): 86−93. WU Yanhua, WANG Fuzhang, LI Fang. Hierarchical planning location model of railway rescue center[J]. Journal of Traffic and Transportation Engineering, 2013, 13(3): 86−93.
[16] 孙剑萍, 宫素萍, 汤兆平, 等. 基于集合覆盖模型的高铁应急资源储备点选址优化[J]. 中国科技论文, 2017, 12(19): 2213−2218. SUN Jianping, GONG Suping, TANG Zhaoping, et al. The site optimization method for the high-speed railway emergency resource storage based on the set covering model[J]. China Sciencepaper, 2017, 12(19): 2213−2218.
[17] 祝蕾. 基于复杂网络理论的城市轨道交通应急救援站选址研究[D]. 南京: 东南大学, 2018. ZHU Lei. Research on location of urban rail transit emergency rescue stations based on complex network theory[J]. Nanjing: Southeast University, 2018.
[18] Revelle C, Toregas C, Falkson L. Applications of the location set-covering problem[J]. Geographical Analysis, 1976, 8(1): 65−76.
[19] Church R L, Meadows M E. Location modeling utilizing maximum service distance criteria[J]. Geographical Analysis, 1979, 11(4): 358−373.
[20] Berman O, Verter V, Bahar Y. Designing emergency response networks for hazardous materials transportation [J]. Computers & Operations Research, 2007(34): 1374− 1388.
[21] WANG Rui, GAO Suixiang, SHI Weiliang. Neighbor search algorithm for maximal arc-covering problem[J]. Computer Simulation, 2014, 31(10): 445−449.
[22] Blanquero R, Carrizosa E, G.-tóth B. Maximal covering location problems on networks with regional demand[J]. Omega, 2016(64): 77−85.
[23] 舒周攀. 基于多方协同的应急服务设施选址模型研究[D]. 武汉: 华中科技大学, 2017. SHU Zhoupan. Research on the location model of emergency service facilities based on multi-party cooperation[D]. Wuhan: Huazhong University of Science and Technology, 2017.
[24] 汤霖, 孟学雷, 郭文博, 等. 基于覆盖理论的铁路救援列车部署方案研究[J]. 铁道科学与工程学报, 2018, 15(6): 1609−1617. TANG Lin, MENG Xuelei, GUO Wenbo, et al. Deployment schemes for securing trains based on covering theory[J]. Journal of Railway Science and Engineering, 2018, 15(6): 1609−1617.
[25] 聂嘉, 赵鹏, 杨浩, 等. 高速铁路动车组运用的研究[J]. 铁道学报, 2001, 23(3): 1−7. NIE Jia, ZHAO Peng, YANG Hao, et al. Study on motor trainset operation in high speed railway[J]. Journal of the China Railway Society, 2001, 23(3): 1−7.
Optimization model of hot standby EMU allocation scheme
XU Heying1, 2, 3, PENG Xiaoqian1, 2, 3, NI Shaoquan1, 2, 3, YANG Xiaojun4, ZHANG Jie1, 2, 3
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China; 2. National and Local Joint Engineering Laboratory of Comprehensive Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China;3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 610031, China;4. Xi’an North Station, China Railway Xi’an Group Co., Ltd, Xi’an 710016, China)
The configuration scheme of hot standby EMU affects the rescue efficiency and plays an important role in ensuring the normal operation order of railway. This paper aims at the determination of the number of hot standby EMUs and the selection of standby location in the configuration scheme. Taking the comprehensive coverage of railway accident risk as the constraint, and taking the shortest average response time and the least configuration cost of hot standby EMUs as the objectives, the multi-objective programming model for the optimization of the configuration scheme of hot standby EMUs was established, and the Pareto solution set of the multi-objective model was designed based on the tabu search algorithm of step-by-step search. Finally, the reliability of the model and algorithm was verified by an example. The results show that the hot standby EMU configuration scheme can meet the different preferences of decision makers, and that the coordinated optimization scheme of the number and location of hot standby EMU configuration can improve the emergency efficiency of hot standby EMU more than the two step-by-step optimization.
hot standby EMU; allocation scheme; multi-objective programming; tabu search; Pareto solution set
10.19713/j.cnki.43−1423/u.T20190999
U279.2
A
1672 − 7029(2020)07 − 1637 − 08
2019−11−13
国家重点研发计划项目(2016YFC0802208);中国铁路总公司科技研究计划项目(P2018T001)
张杰(1977−),男,湖南湘潭人,副教授,博士研究生,从事交通运输规划与管理研究;E−mail:zhangjiebox@126.com
(编辑 阳丽霞)
