基于混合方法的风速预测模型研究
2020-08-07张如九严磊何旭辉李睿东孙颖
张如九,严磊, 2,何旭辉, 2,李睿东,孙颖
基于混合方法的风速预测模型研究
张如九1,严磊1, 2,何旭辉1, 2,李睿东1,孙颖1
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075)
为实现铁路沿线风速的高精度预报,建立若干基于混合方法的预测模型并进行性能比较。采用小波分解(WD)和经验模态分解(EMD)将原始风速序列平稳化,采用神经网络方法(BP, ANFIS和NAR)进行预测,形成6种混合模型:WD-BP,WD-ANFIS,WD-NAR,EMD-BP,EMD-ANFIS和EMD-NAR。引入基于单一方法的预测模型及时间序列模型ARIMA作为对照组,以平均绝对误差、平均绝对百分比误差、均方根误差比较各模型预测精度。研究结果表明:混合模型的预测性能优于单一模型;单一模型中,ARIMA的预测性能优于神经网络模型;混合模型中,WD-ANFIS的预测精度最高。
风速预测;小波变换;经验模态分解;神经网络;时间序列

我国东南沿海处于台风区,经常受到大风侵袭。为了满足东南沿海地区经济发展需求,近年来许多修建在台风区的铁路应运而生。铁路列车在大风环境下运行时,容易产生安全隐患,脱轨和翻车的可能性大大增加[1],危及铁路行车安全。因此,铁路沿线的风速预测,对于列车的安全运行具有重要意义。目前,采用单一方法进行风速预测,能实现的预测精度仅为25%~40%[2],无法满足实际要求。国内外学者提出了多种方法相结合的方式,对风速数据进行分解预处理后再预测,有效提高了预测精度。刘辉等[3]提出一种基于经验模态分解(EMD)与自适应神经模糊推理(ANFIS)的混合方法,通过EMD将风速分解,再利用ANFIS进行风速预测,体现出良好的非平稳风速预测性能。贺坤等[4]利用一种基于集合经验模态分解(EEMD)和遗传算法(GA)优化的BP神经网络(BP)模型,取得了结果稳定、预测精度高的效果。YU等[5]利用EMD,EEMD和自适应噪声的完整EEMD(CEEMDN)进行信号处理,与奇异谱分析(SSA)和埃尔曼神经网络(ENN)相结合,提出了新的混合模型,给出了更准确的预测结果。Cadenas等[6]比较了差分整合移动平均自回归(ARIMA)模型和利用非线性自回归外生人工神经网络(NARX)建立的多元模型,得到了NARX模型预测结果更优的结论。Aasim等[7]探讨了ARIMA模型和基于小波变换(WT)的ARIMA (WT-ARIMA)模型的不足,提出了一种新的基于极大重叠离散小波变换的ARIMA模型,有效提高了超短期风速预测的精度。虽然许多学者提出的混合预测模型能够有效地提高预测精度,但其风速样本点的时间间隔通常选定为10 min[8],15 min[9]乃至1 h[10]。相比于其他工程领域的风速预测特点,铁路风速预测更偏向于对风速序列在将来几秒钟至几分钟内的“短期”计算[3],时间间隔过大的风速预测结果实时性差,并不能为列车的行驶提供参考数据[11]。另一方面,尽管部分模型采取的风速分解方法和风速预测方法已较为成熟,但是对这些模型的对比分析还较少。因此,有必要对各种混合预测模型的短期预测精度进行进一步的研究。针对上述问题,本文采用小波分解(WD)、经验模态分解(EMD)进行风速预处理,采用BP神经网络(BP)、自适应神经模糊推理系统(ANFIS)、非线性自回归神经网络(NAR)进行风速预测,建立若干混合预测模型,并引入基于单一方法的预测模型(Single BP,Single ANFIS,Single NAR)及时间序列模型ARIMA作为对照组,进行仿真试验,以比较各模型的预测性能,寻找最优模型。仿真试验以1 min为时间间隔选取原始风速序列,进行超前一步预测,从而实现在列车行驶至某地之前1 min将预测风速值实时反馈给驾驶室,便于列车针对具体风速情况采取相应调整措施。
1 混合预测模型的建立
混合预测模型的建立过程如下:1) 采用WD和EMD对风速进行预处理,将原始风速序列分解成若干分量;2) 利用BP神经网络,ANFIS和NAR神经网络对各分量分别进行单步预测;3) 将各分量的预测值线性叠加得到最终的风速预测值。基于以上步骤,形成6种混合模型:WD-BP,WD-ANFIS,WD-NAR,EMD-BP,EMD-ANFIS和EMD-NAR。为验证混合模型的预测精度更高这一假设,引入基于单一方法的预测模型(Single BP,Single ANFIS和Single NAR)作为对照组。为比较神经网络模型与时间序列模型的预测性能,引入Single ARIMA作为对照组。对照组各方法均直接对原始风速序列进行预测。最终形成混合预测模型框架及其比较体系如图1所示。
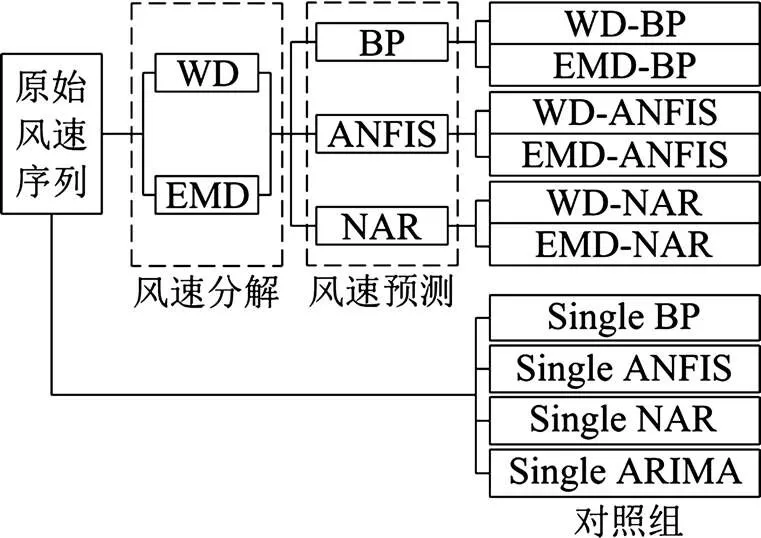
图1 混合预测模型框架及其比较体系
2 实测风速预测
2.1 原始风速序列
为了比较混合预测模型的性能,本文选取2012年台风Bolaven于8月27日00时至16时的实测风速数据进行仿真实验。如图2所示,原始风速序列共900个样本点,样本点时间间隔为1 min,相应采样频率为1/60 Hz。其中,样本点1~800作为训练集,用于训练神经网络;样本点801~900作为测试集,用于获取预测结果,进而比较预测性能。
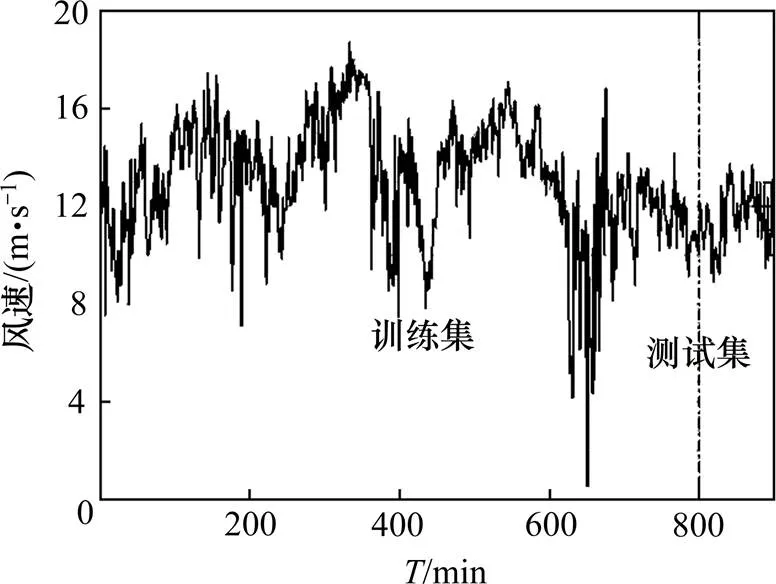
图2 原始风速序列
2.2 风速分解
小波分解可通过MATLAB中的小波工具箱实现。小波基db6,Level选用6,即用db6类型的小波基将原始风速序列分解为1个近似分量(A6)和6个细节分量(D1~D6),分解结果如图3所示。
经验模态分解具有自适应的特点,无需像小波分解那样预先设定分解层数及基函数。缺点是具有端点效应,构成上下包络线的3次样条函数在数据序列的两端出现发散,可能会使得到的分解结果失真[12]。本文采取极值延拓法处理端点效应,对原始风速序列两端进行适当延拓,再将其分解为6个模态序列(IMF1~IMF6)和1个残差序列(Residual),分解结果如图4所示。
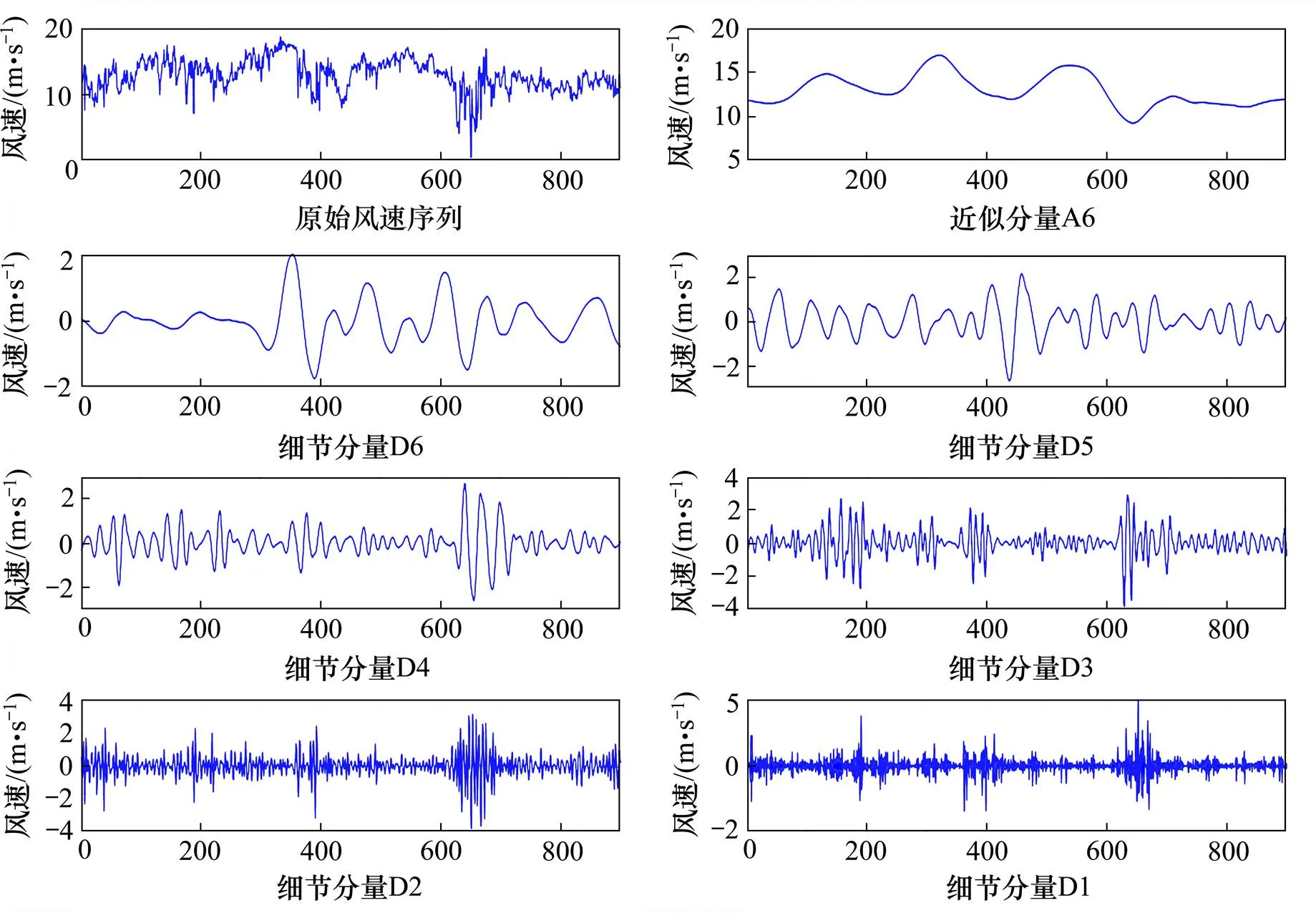
图3 原始风速序列的小波分解结果
2.3 风速预测
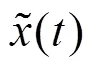
2.4 预测误差
为了比较图1中各模型的风速预测精度,采用3项误差指标:平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)。定义如下:
平均绝对误差
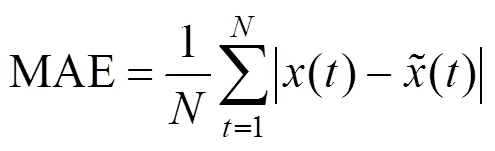
平均绝对百分比误差
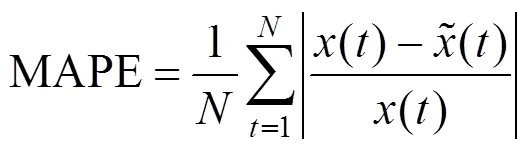
均方根误差
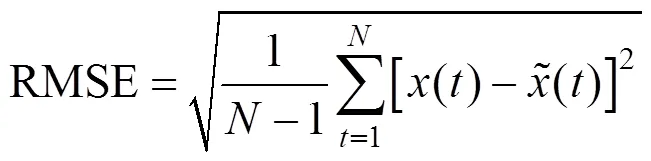
其中:为测试集801~900样本点的实际风速值,为测试集801~900样本点的预测风速值,N为测试集样本数量。计算各模型的MAE,MAPE和RMSE,结果如图6所示。
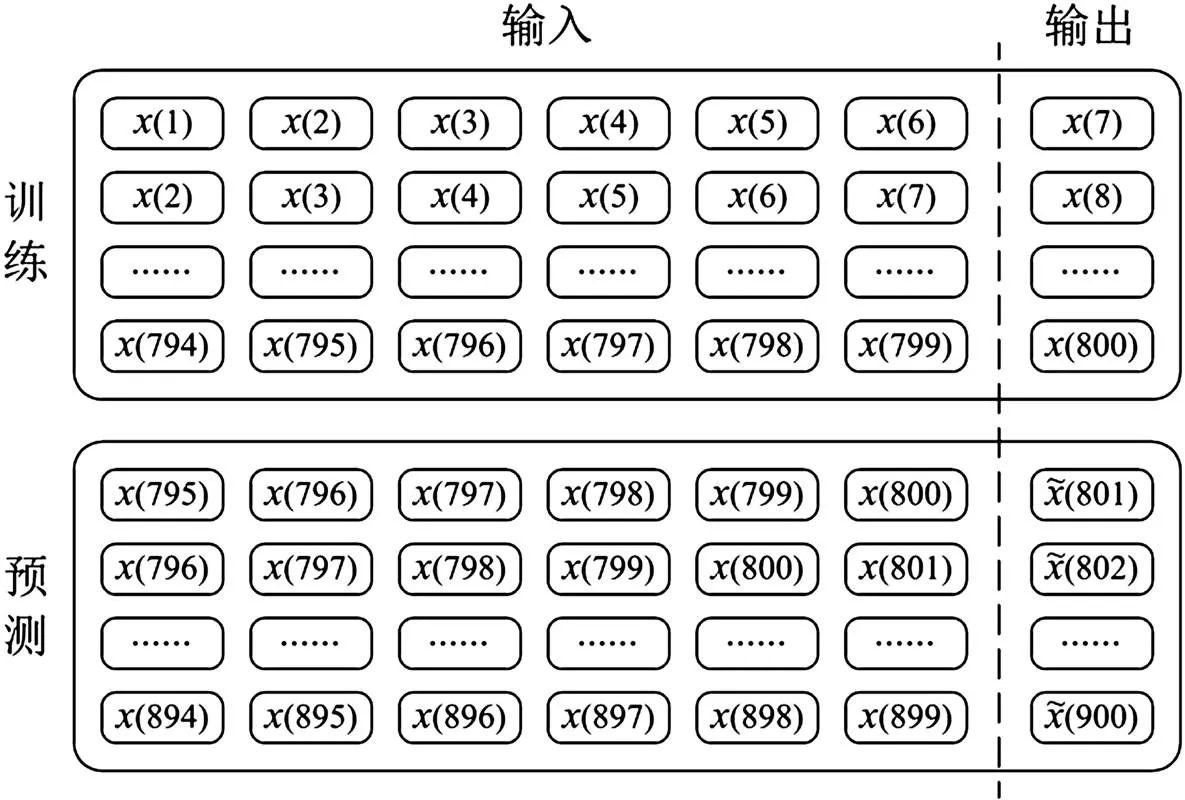
图5 神经网络方法预测过程示意图
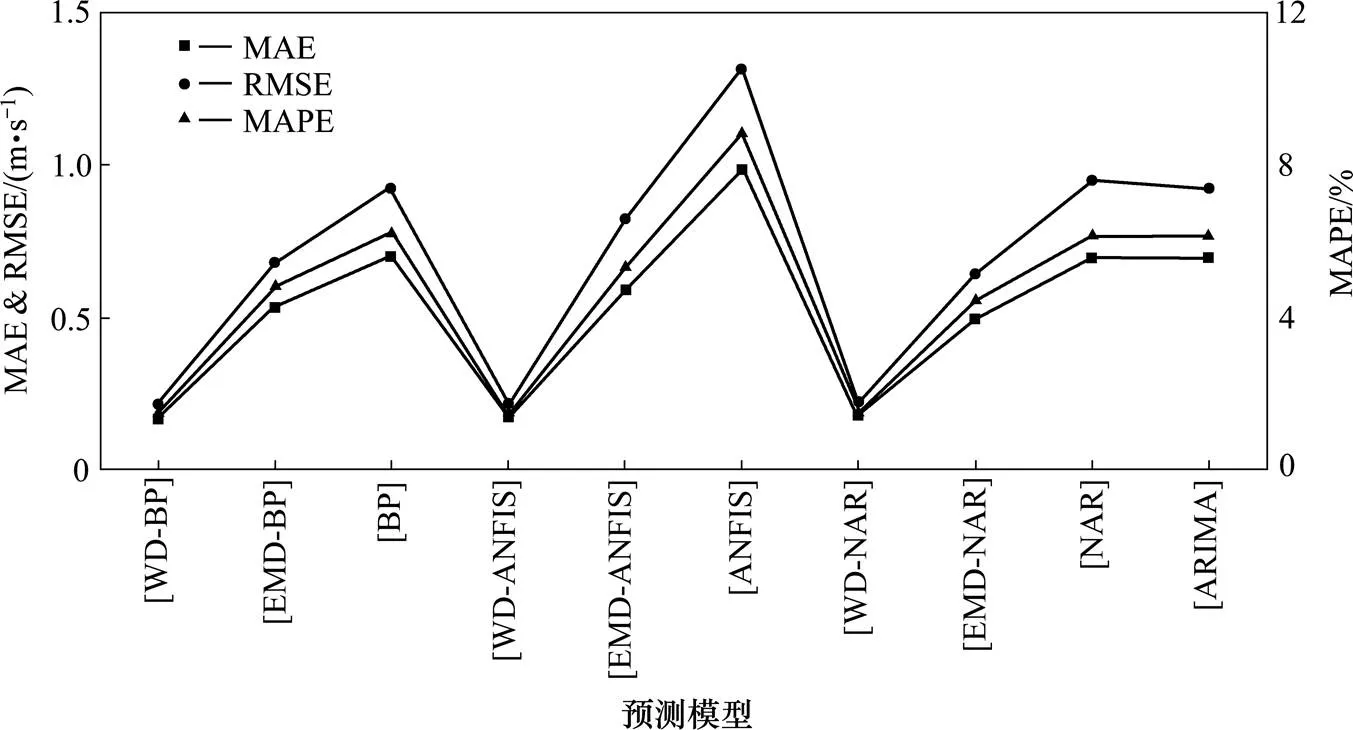
图6 各模型预测误差
3 预测结果的对比与分析
3.1 混合模型与单一模型的预测性能对比
为直观比较混合模型与单一模型的预测性能,取实测值与预测值作图进行对比。从图7可以看出,采用BP神经网络,ANFIS和NAR 3种不同的预测方法时,混合模型的预测曲线与实际曲线的拟合度均较高,而单一模型的预测曲线与实际曲线的拟合度均较低,且在极值点处均存在较大偏离。另外,图7(b)中单一模型Single ANFIS的预测值在某些突变的风速样本点处甚至完全偏离于实测值。
由表1的具体误差可知,采用BP神经网络预测时,单一模型的MAE,MAPE,RMSE达到0.708 m/s,6.237%和0.925 m/s,大于混合模型WD-BP和EMD-BP的3项误差指标。采用ANFIS预测时,单一模型的MAE,MAPE和RMSE达到0.986 m/s,8.820%和1.318 m/s,也远大于混合模型WD-ANFIS和EMD-ANFIS的3项误差指标。采用NAR预测时,单一模型的误差同样较大。
综合以上分析可知,预测方法分别采用BP,ANFIS和NAR时,混合模型均表现出更优越的预测性能。说明对非平稳风速序列进行分解预处理后再预测,有效提高了预测精度。
3.2 神经网络与时间序列模型的预测性能对比
由图8可知,神经网络和时间序列模型的预测值均与实测值有一定的偏离,其中Single ANFIS偏离很大,预测精度较低。由表2可知,模型Single BP,Single NAR的3项误差仅略大于Single ARIMA,故无法比较BP,ANFIS和ARIMA的预测性能。
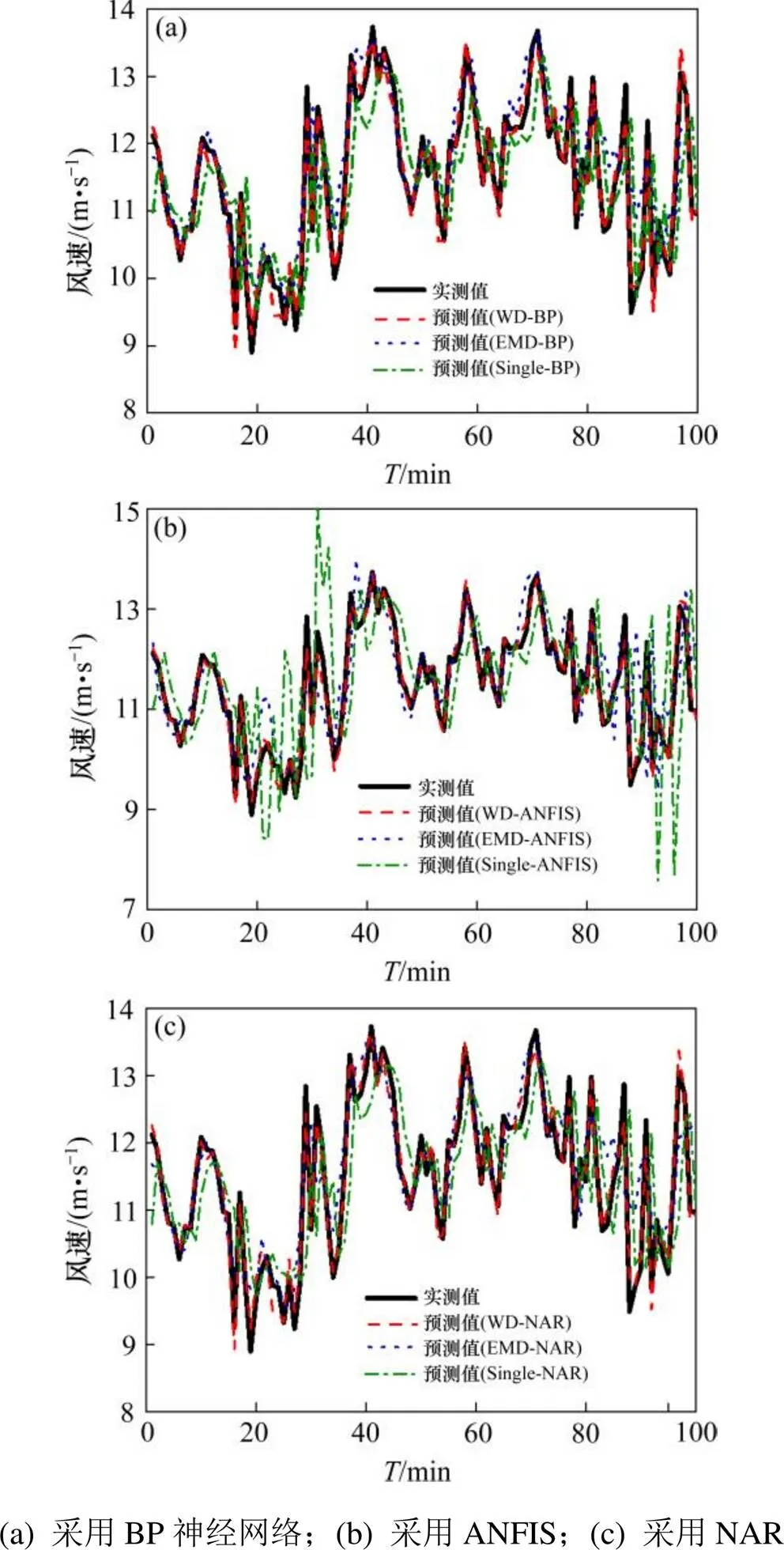
图7 混合模型与单一模型的预测结果

表1 混合模型与单一模型的预测误差
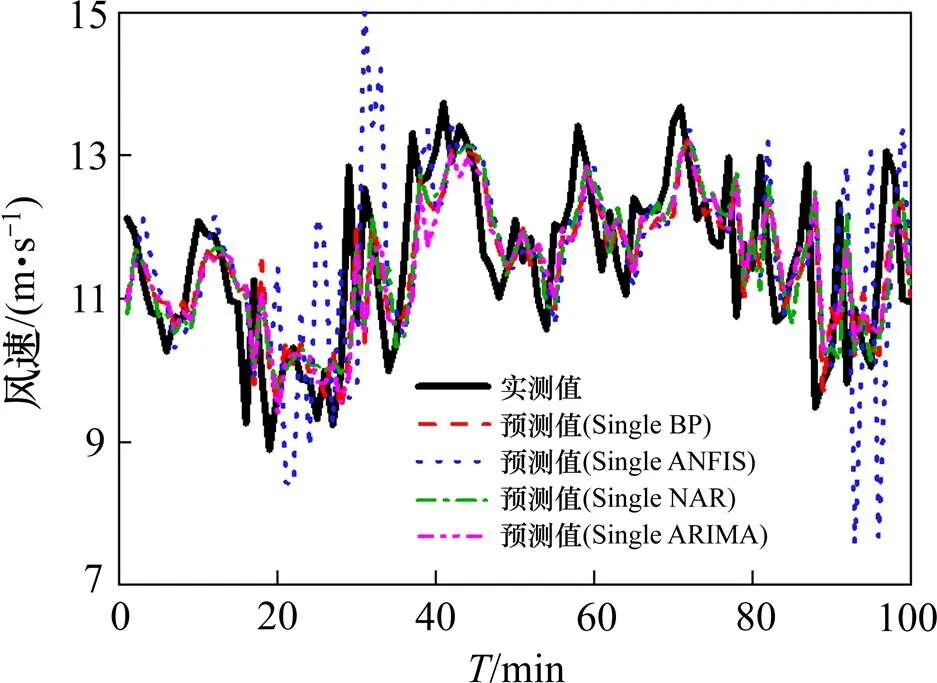
图8 神经网络模型与时间序列模型的预测结果

表2 神经网络模型与时间序列模型的预测误差
然而,神经网络的预测结果具有不唯一性,单次训练可能会产生较大的误差。对于某些特征样本,神经网络在训练时会产生严重的过拟合,测试集又仅包含少量的训练集特征,导致部分预测值成为离群点,与实测值偏离很大,因此模型的鲁棒性相对较差。而时间序列ARIMA模型依靠内生变量,通过差分将原始数据平稳化,能够快速得到唯一确定的预测结果,鲁棒性相对较好。因此从模型鲁棒性的角度可认为,采用单一模型时,ARIMA的风速预测性能更优。
3.3 混合模型的预测性能对比
从图9可以看出,采用WD的神经网络模型,其预测值与实际值基本吻合;采用EMD的神经网络模型,其预测值在部分样本点处与实际值有少量偏离。由表3也可以看出,采用WD的混合模型的预测误差远低于采用EMD的混合模型。其主要原因是EMD会产生模态混叠现象,原始序列中存在干扰与噪声会影响到极值点的选取与包络线的拟合,进而导致在同一个IMF中出现差异很大的特征尺度,或相近的特征尺度出现在不同的IMF中,难以充分发挥风速预处理对预测精度的提升作用。
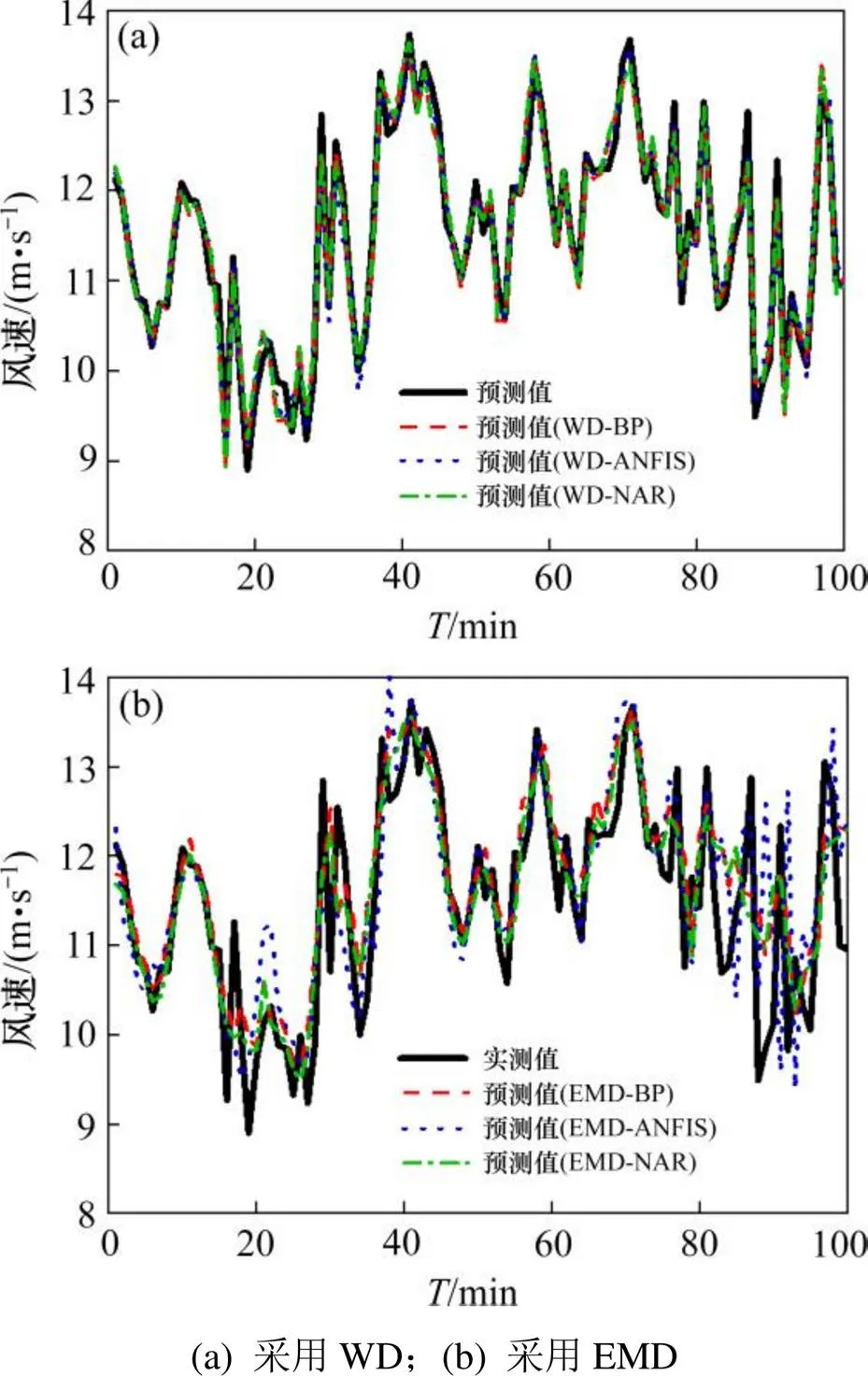
图9 神经网络模型的预测结果
表3中WD-ANFIS的MAE,MAPE和RMSE分别达到0.169 m/s,1.482%和0.220 m/s,在所有模型中误差最小,预测性能最好。采用WD进行风速预处理不存在模态混叠问题,ANFIS能够结合模糊系统与神经网络两者的优点,运用最小二乘法和BP算法的组合算法进行学习,WD-ANFIS模型有效提高了预测精度,且具有一定工程应用价值。
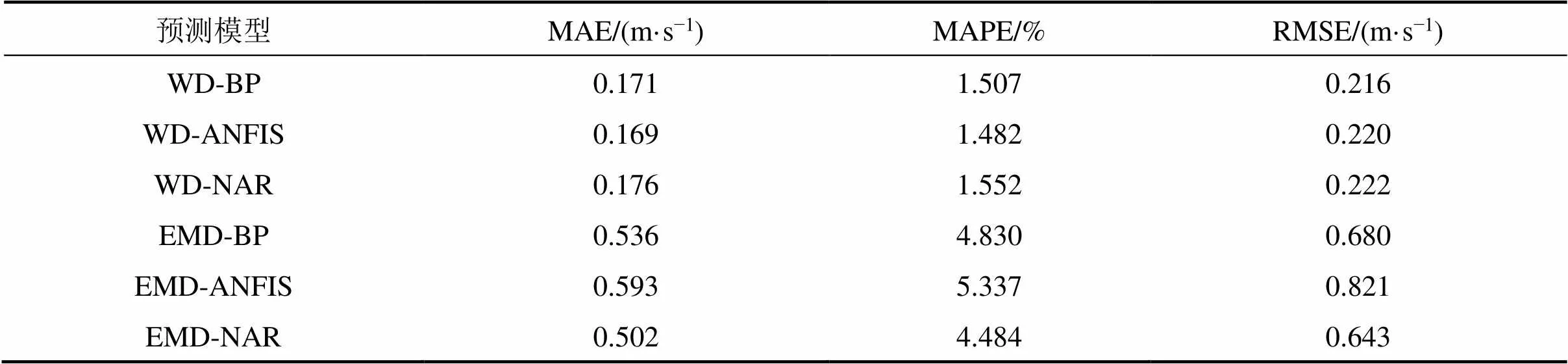
表3 混合模型的预测误差
4 结论
1) 采用WD和EMD进行风速预处理,采用BP,ANFIS和NAR 3种神经网络方法进行预测,建立了若干混合预测模型,并引入单一模型和时间序列模型ARIMA作为对照组,对各模型进行了预测性能的多层次比较。
2) 预测方法分别采用BP,ANFIS和NAR时,混合模型均表现出更优越的预测性能。
3) 单一模型中,时间序列模型ARIMA的风速预测性能更优。
4) 混合模型中,采用WD的混合模型的预测性能普遍优于采用EMD的混合模型,其中模型WD-ANFIS的预测精度最高,将其应用于铁路沿线的风速预测,可实现超前1 min的高精度预报。
[1] 任尊松, 徐宇工, 王璐雷, 等. 强侧风对高速列车运行安全性影响研究[J]. 铁道学报, 2006, 28(6): 46−50. REN Zunsong, XU Yugong, WANG Lulei, et al. Study on the running safety of high-speed trains under strong cross winds[J]. Journal of the China Railway Society, 2006, 28(6): 46−50.
[2] 叶林, 刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报, 2011, 31(31): 102−108. YE Lin, LIU Peng. Combined model based on EMD-SVM for short-term wind power prediction[J]. Proceedings of the Chinese Society for Electrical Engineering, 2011, 31(31): 102−108.
[3] 刘辉, 张雷, 田红旗, 等. 基于经验模式分解和自适应神经模糊推理的风速短期智能预测混合方法[J]. 中南大学学报(自然科学版), 2016, 47(2): 676−682. LIU Hui, ZHANG Lei, TIAN Hongqi, et al. Short-term wind speed intelligent prediction method based on empirical mode decomposition and adaptive neural fuzzy inference system[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 676−682.
[4] 贺坤, 李星野. 基于经验模态分解和遗传算法改进的神经网络模型的风速时间序列预测[J]. 电子测量技术, 2018, 41(8): 146−149. HE Kun, LI Xingye. Wind speed forcasting based on EEMD-GA-BP[J]. Electronic Measurement Technology, 2018, 41(8): 146−149.
[5] YU Chuanjin, LI Yongle, ZHANG Mingjin. Comparative study on three new hybrid models using elman neural network and empirical mode decomposition based technologies improved by singular spectrum analysis for hour-ahead wind speed forecasting[J]. Energy Conversion and Management, 2017(147): 75−85.
[6] Cadenas E, Rivera W, Campos-Amezcua R, et al. Wind speed prediction using a univariate ARIMA model and a multivariate NARX model[J]. Energies, 2016, 9(2): 1−15.
[7] Aasim, Singh S N, Mohapatra A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting[J]. Renewable Energy, 2019(136): 758−768.
[8] ZHANG Yagang, CHEN Bing, PAN Guifang, et al. A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting[J]. Energy Conversion and Management, 2019(195): 180−197.
[9] PEI Shaoqian, QIN Hui, ZHANG Zhendong, et al. Wind speed prediction method based on empirical wavelet transform and new cell update long short-term memory network[J]. Energy Conversion and Management, 2019(196): 779−792.
[10] YU Chuanjin, LI Yongle, BAO Yulong, et al. A novel framework for wind speed prediction based on recurrent neural networks and support vector machine[J]. Energy Conversion and Management, 2018(178): 137−145.
[11] 魏昱洲, 许西宁. 基于LSTM长短期记忆网络的超短期风速预测[J]. 电子测量与仪器学报, 2019, 33(2): 64− 71. WEI Yuzhou, XU Xining. Ultra-short-term wind speed prediction model using LSTM networks[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(2): 64−71.
[12] 舒忠平, 杨智春. 抑制经验模分解边缘效应的极值点对称延拓法[J]. 西北工业大学学报, 2006(5): 639−643. SHU Zhongping, YANG Zhichun. A better method for effectively suppressing end effect of empirical mode decomposition[J]. Journal of Northwestern Polytechnical University, 2006(5): 639−643.
Research on wind velocity prediction models based on hybrid methods
ZHANG Rujiu1, YAN Lei1, 2, HE Xuhui1, 2, LI Ruidong1, SUN Ying1
(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410075, China)
In order to achieve high-precision forecasting of wind speed along the railway, several prediction models based on hybrid methods were established with their performances compared accordingly. First, the wavelet decomposition (WD) and empirical mode decomposition (EMD) methods were used to stabilize the original wind speed series. Then, neural network methods (BP, ANFIS and NAR) were used for predictions, forming six hybrid prediction models: WD-BP, WD-ANFIS, WD-NAR, EMD-BP, EMD-ANFIS and EMD-NAR. Several prediction models based on a single method and the time series model ARIMA were introduced as a control group, and the prediction accuracy of each model was compared in terms of the average absolute error, the average absolute percentage error, and the root mean square error. Research results show that predictionperformance of hybrid models is better than that of single models. Among single models, the prediction performance of ARIMA is better than that of the neural network model. Among hybrid models, the prediction accuracy of the WD-ANFIS model is the highest.
wind speed prediction; wavelet transform; empirical mode decomposition; neural network; time series
10.19713/j.cnki.43−1423/u.T20200268
U298.1
A
1672 − 7029(2020)077− 1630 − 07
2020−04−05
国家自然科学基金资助项目(51808563,51925808);交通行业重点实验室开放课题资助项目(KLWRTBMC18-03)
严磊(1988−),男,湖南华容人,讲师,博士,从事桥梁风工程研究;E−mail:leiyan@csu.edu.cn
(编辑 蒋学东)
