以核心问题为驱动引领学生探究学习

陈华忠

深度学习的课堂，既包括教师设计具有挑战性的学习素材引发学生的深度思考，又包括学生在学习中不断深入探讨数学的本质，提出有价值的数学问题，或在学习中生成有价值的数学问题。那么，以问题为驱动，引领学生积极参与，主动探究，同时也让学生体验知识形成过程，从而理解与掌握所学新知。

一、围绕核心问题，探究概念本质

依据教材内容，挖掘一两个核心问题，并围绕核心问题，引领学生自主探究。在探究学习中，学生的思维随时随地都会迸发智慧的火花。如何在枯燥的概念教学中突现概念本质属性呢？真正做到围绕核心问题，引领学生探究数学概念的本质。

如，在教学“三角形的三边关系”一课时，上课伊始，教师先让学生猜想，给你三根小棒能否围成一个三角形？学生在潜意识里认为是可以的，但也有部分学生存有疑问。然后，放手让学生拿出学习袋里的小棒，以小组为单位进行合作探究，有的动手去围，有的记录，有的计算，有的帮忙围。通过操作探究，发现有的能围成三角形，有的却不能。并指名汇报：

生1：我们小组的三根小棒能围成三角形，三根小棒的长分别是3厘米、6厘米、8厘米。

生2：我们小组的三根小棒也能围成三角形，三根小棒的长分别是3厘米、7厘米、9厘米。

师：这两组的三根小棒都能围成三角形，它们有没有共同的特征？

引导学生观察、比较并发现：两边之和大于第三边。

师：有没有围不成的？

生3：我们小组的三根小棒不能围成三角形，三根小棒的长分别是3厘米、7厘米、12厘米。无论怎样摆，都无法围出一个三角形。

师：问题出在哪里？

生：给的两根7厘米与3厘米太短了。

此时，师引导学生：这两根太短了些，那我们试着把这两根小棒往下按会怎样呢？如果一直按下去直到这两根小棒成一直线还会围成一个三角形吗？这说明了什么？在操作中让学生深刻体会到这短的两根小棒长度之和小于第三根小棒长度，不可以围成一个三角形，从而建立起两边之和要大于第三边的表象。

师：若让你们调整1根或2根小棒，你能围成一个三角形吗？不管是能围成还是不能围成，请你们把调换后的三根小棒的长度记录下来;然后小组讨论：从围成的三角形的三根小棒的长度中，你们发现了它们之间有什么共同的特点？在反馈中引导学生形成共知：三角形的任意两边之和大于第三边。然后，在巩固练习时，出示三根小棒的长度，让学生很快判断是否能围成三角形？并概括出两条短边之和大于长边，就能围成三角形，从而牢固地掌握所学知识。

二、围绕核心问题，深究计算算理

“算理”顾名思义指的是计算的方法和原理，运算的正确是建立在透彻地理解算理的基础上。有句古话说得好，“知其然，而知其所以然”，计算的学习亦是如此，“知其然”是会算，知道怎样算，而“知其所以然”是理解、掌握为什么这么算，只有达到“知其所以然”，才能弄清计算的算理。

如，在教学“9+几=”一课时，让学生计算出结果，其实并不难，许多学生都会计算，但对算理的理解却有一定的困难。学生往往“知其然而不知其所以然”。显然，引导学生探究理解“9加几的算理，发展学生的思维能力”是这一节课的重点。教学中，可设计如下的互动过程：师生共同列出算式：9+6。师问：“那么结果是多少呢？”很多学生说是15。教师提出一个核心问题：“那么9+6为什么等于15？ 你是怎样想的？学生开始寻求证明自己答案的途径和方法。此时，教师引导学生通过互动，展示不同的思考方法，可以是口头表达，也可以借助直观教具，通过学生动手操作，而学生操作演示的过程正是学生弄清算理的过程，从而帮助学生深入地理解“9+几”的计算算理。

三、围绕核心问题，探究数学规律

高斯说：“数学中的一些美丽定理具有这样的特性：它们极易从事实中归纳出来，但证明却隐藏得极深。”“找次品”是公认的教学难题，尤其是在原理的分析上难度特别大，李衡校长执教这一节课时，她在教材上分析、挖掘很到位，在教学设计上很精细，对探究规律上很开放，在教学调控上很灵活，给我们上了一节很好的示范引领课。

如，李校长执教“找次品”一课时，她让学生充分经历“比较——猜测——验证”的探究过程，理解找次品的最优策略。当李校长介绍完天平的特点和作用后，便带领一群小数学家通过几个核心问题进入探究规律的活动中：

1.核心问题①：怎样在3个物品中找一个次品（至少称几次才能保证找到次品），这里的“至少”和“保证”是什么意思？（考虑的是最不利的因素）

2.核心问题②：怎样在8个物品中找次品（8个中有一个较轻，至少称几次才能保证找到次品）。

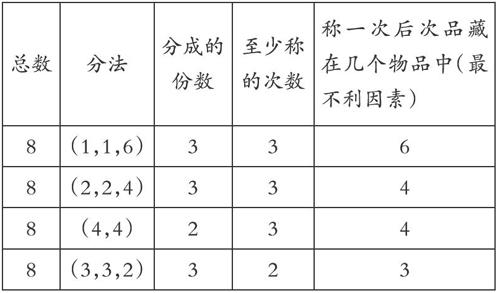
师：我们先称一次，可能会怎么分？至少称几次才能保证找到次品？分析：考虑最不利因素，第一次称完后次品应该藏在几个中？（师生逐步归纳出这份表格进行观察）

3.核心问题③：每次每边称4个的小组为什么反而不如每次每边称3个的小组完成得快？学生进一步讨论：为什么用8（3，3，2）的方法最快找到次品？

4.核心问题④：通过对比称完一次后的情况，你能发现什么？?称完一次后，次品藏在6个，4个，4个，3个中，我们从剩下最多的情况有四种，找出最少的情况（从剩下3个中找）就是通过枚举法，从多中找少（体现至少），算出称最少次数又能保证找到次品。?

这样，学生初步得到一个结论：把待测物体分3份，尽量平均分。在验证环节：当我们用9个、10个、11个来验证这个结论时，学生自然很快想到平均分成3份的方法，也能进行说理。

5.核心问题⑤：如果我们不知道次品是较轻还是较重，你怎么找次品呢？请有兴趣的同学回家思考。

学生们经历了这样的数学活动与思考，思维会不断深入，不断拓展，数学素养会不断提升。如“称一次后次品藏在几个物品中”这个问题提得非常有价值，它是理解“为什么要均分三份”这个規律的关键。又如“多中找少”这个环节对“至少，保证”进行阐述，进一步突破文字理解的难度，为后面解决更多的问题扫清障碍。教材中的“找次品”是一种理想化的问题，把不知轻重的问题留给学生思考，给学生更大的想象空间，可以使有余力的学生思维能力得到更大的发展。像这样层层递进，逐渐感知理解找次品的最优策略的教学方法不断给学生视觉和思维上的冲击，学生在积极参与，自主探究，合作交流中提高了课堂学习效率，提高了学习能力。对比其他不重过程，不深究数学思考中的本质问题，急于得到结论而把结论进行优化的方法来说，我觉得用围绕核心问题探究数学规律更能激发学生挖掘数学背后真相的好奇心，更能促进学生对数学本质的理解，启迪学生的思维。