深度思考——让学生的数学学习从肤浅走向深刻

匡元霞

摘 要：在小学数学课堂教学过程中，不仅需要让学生主动参与到课堂中来，更需要关注其思维参与的程度，思维的参与程度决定着学生获得知识的再生能力。在教学过程中，通过让学生提取相关知识解决问题，让学生经历知识形成的过程，以及让学生选择解决问题的策略等方法，让学生深度参与到课堂中来，学生的思维才会逐步从由肤浅走向深刻。

关键词：主动提取;经历过程;策略匹配

小学生的数学学习离不开思维的参与，学生思维的参与程度决定着学习过程的质量，也决定着学生获得的知识是否具有生命力。在教学过程中，给予学生适度的思维空间，让学生进行深度思考，有利于培养学生思维的深刻性，达到对知识的深度理解，提高知识的再生能力。在课堂教学过程中，如何让学生进行深度思考呢？下面从以下几个方面谈谈常见的一些做法。

一、深度思考——学生主动提取旧知以解决新问题

在计算学习的过程中，在课的开始，常常复习与新知有关的旧知，夯实本节课的知识基础。学生学习的初始阶段，由于学习经验不足，容易遗忘旧知，在计算课的开始，适当复习是必要的，也是必须的。但是如果老师在教学过程中使用一成不变的模式，先安排好复习内容，然后再学习新知，这样的学习过程容易让学生形成思维惰性，不能主动从头脑里提取与新知有关的旧知来解决问题。在学生对旧知掌握得较好的基础上，可以适当撤除课前的复习，在课堂上安排适当的环节让学生主动提取与之相关的经验来解决问题。

在教学“除数是整十数商是两位数的除法”的过程中，在学生能够运用估算以及乘除法之间的关系确定商的范围后，再和学生一起研究用竖式计算的方法。看到商在十位上的时候，让学生想想：为什么商在十位上？学生会有一种感觉是估一估，知道商是几十多，所以商在十位上，还要继续追问：你是怎么想到的？有的学生会根据数的组成来思考;还有的会根据前面学习的两位数除以整十数来思考，根据96÷20，想到这个算式的计算过程（如图1）。

在这个环节中，撤除了前面的复习过程，通过课堂中间一个简单问题的回顾，一方面复习了前面的笔算方法，另一方面也让学生获得了学习新知的方法，运用类似经验来解决新问题，建构新知识。从学生学习心理学的层面来分析，如果学生提取经验的时间越长，这样的过程给学生留下的印象越深刻。

二、深度思考——学生经历“数学常识”的探索过程

数学中许多隐藏于数学问题背后的规律、性质等都可以让学生经历一个探索的过程，形成对于问题的深度认识。但是，一些数学常识常常被我们忽视，这种忽视的结果是学生对概念没有留下深刻的印象，遗忘的概率比较高。在一些数学常识学习的过程中，一些看起来没有探索价值的内容，我们仍然可以安排让学生经历探索过程，让学生在探索过程中通过自己的理解形成对问题的深度认识。

在“平年与闰年”的教学过程中，首先让学生观察近几年2月份的日历，在学生找到了平年和闰年之后，再去发现有什么排列规律？学生能够理解3个平年后面连着一个闰年，也就是每4年里面有一个平年也有1个闰年，4个一组。然后让学生想一想：找到了这样的规律，那么闰年的这个数怎么来安排呢？这其中有生活的经验，也有数学中合理的成份。所以，我们要带着学生体验一下这样规定的道理是什么？让学生结合前面一个数除以4的经验来思考：一个数除以4，它的余数有1、2、3和没有余数4种，让什么样的数可作为闰年呢？让学生想一想：这里什么样的数作为闰年比较适合？学生能够理解要与前面的规律匹配，当然把没有余数的那一年作为闰年，有余数的作为平年。然后利用刚才的经验算一算年历中的年份，看看我们通过这种方法判断的结果和实际的结果是否吻合？并且生成相应的判断方法，一个是根据2月份的天数直接判断是平年还是闰年，另一个是根据平年和闰年排列的规律来判断，因为3个平年和1个闰年，这里的3和1作为一组，一组的和是4，所以根据一个数除以4的4种情况分成两类，与排列规律对应。

上述过程中，4年中有3个平年和1个闰年，到底把哪个年份作为平年，哪个作为闰年，这个规定的过程要与学生的认知匹配。要让学生体会到生活中数学知识的运用，现象本身的规律与数学内部知识吻合的时候，就可以运用相应的数学模型去解决问题，把数学知识还原到教育形态，促进学生的深度思考。

三、深度思考——策略与问题的匹配

数学是好玩的，好玩在哪里？最重要的是解决问题的策略不是一成不变的，不同的问题可以有不同的解决问题的策略，更重要的是以前简单的思路，现在不一定就是简单的思路了。在这里，有一个重要的思路就是问题与策略的匹配。

例如下面一题的教学（如图2），这是一个连乘实际问题，一般情况下，学生会想到两种不同的思路来解决这个问题：一个是先算出每人5天能组装多少台电脑，再求4人5天一共可以组装多少台电脑;另一个是先算出4人每天能组装多少台电脑，然后再算出4人5天一共能组装多少台电脑。通过比较，学生也体会到这两种方法都可以求出一共组装了多少台电脑。在后续的练习中，学生也基本形成了这样一个认识：像这样的问题，我们一般都有不同的思路来解决问题，同时还要注意列出的算式要与思考问题的思路匹配。形成定势是便于形成解决问题的技能，但是又不能仅仅拘于技能。我们在教学过程中，要打破这种思维定式，让学生体会到解决问题的策略不是一成不变的。

明光小学新建一幢4层的教学楼，每层有5个教室，

每个教室放24张课桌。一共需要多少张课桌？

在后续教学另一道题的过程中（如图3），在求一共需要多少张课桌的时候，学生根据前面学习的经验，一種方法可以先算一共有多少间教室，再求20间教室一共需要多少张课桌;还可以先算1层有多少张课桌，再求4层有多少张课桌。这道题是在学生学习了运算律之后再遇到的题目，仍然让学生通过两个思路来完成，显然不是本题的最终目的。所以引导学生去比较：这两种方法虽然都能求出一共有多少张课桌，但是哪一种方法比较方便呢？再拉出以前的学习过程，为什么以前我们用两种方法都可以，而这道题却觉得用第一种方法比较简便，在这里，着重让学生体会到思路是有数据限制的，思路的简便要与问题情境里的数据匹配，根据题目里的数据选择合适的思路。

深度思考其实是解决问题的策略与具体问题的匹配，在不同的问题情境中能够找到最合适的、最便捷的解决问题的思路，当把数学看成运用一成不变的思维模式去解决问题的时候，这就严重影响学生的深度思考。数学运算的程序是必需的，但是程序的选择更重要。

四、深度思考——让学生在运用中体会到知识的价值

新知引入的过程中，常常安排丰富的学习过程，让学生经历知识的产生过程，理解知识的价值。但是，在后续解决问题的过程中，常常是机械地执行相应的程序，无法体会到知识的价值。所以，在学生练习的过程中，需要通过不断强化，让学生主动运用相关知识解决问题，体会知识的价值。

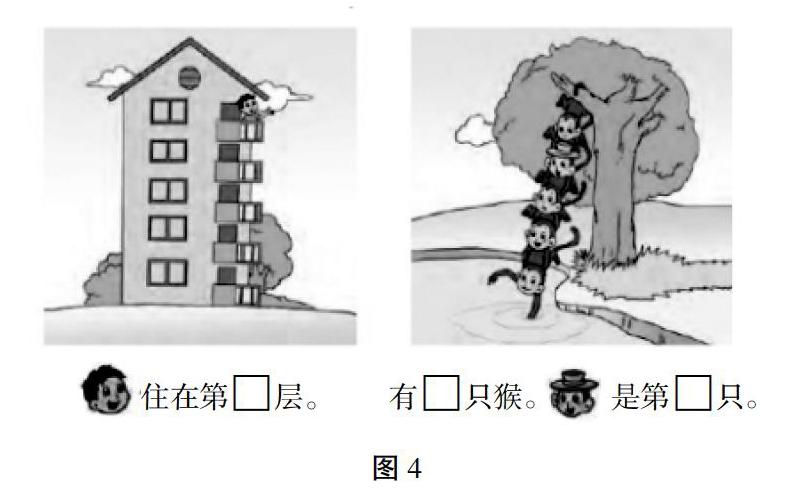
在“认识几和第几”的练习过程中（如图4），对于第一题的处理过程，大部分老师直接告诉学生：一般我们在数楼房层数的时候是从下往上数的，数一数，小朋友住在第几层？这一题的处理就到此结束了。这里，学生只是体会到了运用自然数的序数意义去描述生活中有序排列的现象，并没有真正体会到自然数作为序数的价值。

在学生初步认识自然数序数意义的过程中，可以采用以下的教学方式让学生初步体会到自然数作为序数的作用：（1）首先让学生看一看这个楼房，并且数一数，这个楼房一共是多少层？（2）让学生体会到小男孩住在这个楼房的最高层;（3）想一想：怎么样让别人知道小男孩住在楼房的最高层呢？在前面学习经验的启发下，学生自然想到运用第几层描述，此时，老师再规范学生的描述方式，对于楼房的层数，我们一般是从下往上去数;（4）去掉图，让学生闭着眼睛想一想：一幢楼房一共是3层，小男孩住在第3层，你能够想象出他的位置吗？他住在第1层呢？第2层呢？通过上述这样4个层次的学习，不仅让学生学会了运用自然数的序数意义去描述生活中的有序事情，而且体会到了自然数的序数意义在描述生活中有序事情的价值。

如果对于自然数序数意义的教学仅仅停留于此，那么就不能充分体会到运用自然数描述生活中有序事情的优势。在后续学习过程中，也可以让学生学会运用其他有序排列的符号去描述生活中有序排列的现象，如甲、乙、丙、丁、A、B、C、D等，通过描述方式的比较，让学生进一步清楚运用自然数的序数意义去描述生活中有序事情的现象，可以更加方便地进行序数与基数之间的转换。

知识价值的体现，不仅指不断重复运用，更是在不断运用的过程中不断拓展知识的外延，加深对某一知识本质的把握，在后续学习过程中，能够主动创造相应的知识去解决问题，提升知识的再生能力。

总之，在小学数学课堂教学过程中，教师不仅需要让学生的思维主动参与到课堂中来，更需要关注思维参与的程度。在教学过程中，教师通过让学生自己提取相关知识解决问题，让学生经历知识形成的过程，以及让学生选择解决问题的方法，给学生探索的空间，让学生深度参与到课堂中，学生的思维才会逐步从肤淺走向深刻。

参考文献：

[1]史宁中.基本概念与运算法则[M].北京：高等教育出版社，2013.

[2]史宁中.数学思想概念（数量与数量关系的抽象）[M].吉林：东北师范大学出版社，2008.