初中数学教学中学生思维能力培养之我见

摘要：抽象难以理解的数学知识，层层迷雾的数学问题，皆需要学生具备较强的数学思维能力进行学习和解答。初中生正处在数学打基础的重要阶段，也是思维能力培养的关键时期，实践教学中，教师要高度重视对学生数学思维能力的培养，从而筑牢数学基础。文章从注重优良思维习惯培养、设置开放性问题、加强解题思想方法指导三个方面入手，对初中数学教学中，学生数学思维能力的有效培养策略进行探究，旨在不断提升学生的数学思维品质。

关键词：初中数学;思维能力;习惯;意识;思想;兴趣

思维能力培养是数学课堂教学目标的重要内容。初中数学教学切实培养学生的数学思维能力，教师要侧重从学生思维的灵活性方面加以引导，精心设计课堂教学，从学生的思维积极性和认真程度、思维意识和习惯、思想方法和策略等方面着手，有侧重地引导学生锻炼思维的灵活性，促进学生数学思维由低阶向高阶发展，从而不断提高学生的数学学习能力。

一、 注重优良思维习惯培养，强化数学意识

初中生正处在思维培养和发展的最佳时期，思维的灵活性对学生的学习和数学能力的发展有着较大的影响，培养学生灵活的数学思维，需要首先培养学生具有良好的思维习惯，良好的思维习惯可以促进学生保持一贯的思维灵活度，促进学生养成良好的思维意识。实践教学中，教师应侧重引导学生利用数学习题鼓励学生在学习和思考中学会创新，以此来培养学生养成良好的思维习惯，强化数学意识。

（一）引导学生积极进行思考

思维懒惰在初中阶段的学生中普遍存在，尤其是对于数学学科的学习，本来较聪明的学生，因为感觉动脑筋思考问题会很累，以至于不爱思考，严重桎梏了学生学习成绩的提高。因此，教学中教师要侧重培养学生积极思考的良好习惯。初中数学知识存在一些抽象性问题，且其思维训练的难度使得许多学生在学习中产生了畏难情绪，打击了学生在课程学习中的参与积极性，不利于学生数学思维的发展和成熟。课堂上，引导学生积极进行思考，教师可借助有趣的问题营造浓厚的学习氛围，促进学生积极参与学习。例如，方程x3-ax2-2ax+a2-1=0有且只有一个实数根，请求出a的取值范围。学生求解这一问题时，大多会从未知数x的角度来解答，却又不知如何求解。教师可顺势启发学生：“大家不妨采取降幂的办法解答。”学生立刻想到了因式分解或者运用换元的办法，可是尝试多次后，一直未能有效取得突破，原因是学生皆是从x的角度入手。在学生想要放弃时，教师及时提示：“x无法进行解答，何不对a下手呢？”话音刚落，学生恍然大悟，有的拍头如梦初醒，之前的一筹莫展都变成了满面笑容，跃跃欲试进行解答，最后从a入手分解因式，原式化解为（a-x+1）（a-x2-x-1）2=0，最后顺利得解。

（二）培养学生认真学习习惯

认真审题、认真计算、认真书写、认真反思等学习数学所需要的良好认真习惯，是推动学生数学思维有效发展的重要保障。在日常课堂教学和学生课后自主学习中，教师需通过引导学生认真的观察习题，通过认真观察全部条件来积极思考解答问题，最后反思发现自身学习中存在的不足，以此来促进学生自身学习质量的提升，推动数学思维的发展。因为解答数学问题，首先要认真观察才能准确地审好题，培养学生认真观察的习惯，教师应设计具有“陷阱”的习题，进而有针对性地锻炼学生的认真观察习惯。例如，在一元二次方程（x-2）（x-1）+1=x的解题过程中，学生若是观察不仔细，则可能会通过去括号、移项，以及合并同类项等方式来完成计算，计算量较大，无形中增加了解题的难度，容易在计算中出现错误。在实际解题中，教师应引导学生认真观察题目的结构，将右侧的项移到左侧，形成（x-1）（x-3）=0的结构，这样可以快速地得出问题的答案，且准确性更高。在数学学习中，借助认真观察来发现更为灵活的解题方式是推动学生数学思维灵活性发展的有效手段。

计算能力是数学学科核心素养的重要内容，计算和书写同样需要学生养成良好的认真习惯。往往有部分学生在观察审题环节已经找到正确的解题思路，然而在计算书写中出现错误。因此，引导学生对数学问题进行分析解答计算的过程中，教师要引导学生全面了解题目的已知条件，充分发挥思维的主动性联系已有的知识结构，对需要求解的问题认真思考其内涵和外延，加强学生精力集中程度的锻炼，做到按审题思路步骤清晰、准确、无误地计算，做到不漏解，不多解，不误解。

（三）促进学生开展多向思考

数学问题往往具有多种解题策略，只有找准最为简捷的解题方法，才会提高解题的效率。因此，教师在日常教学中应有侧重地引导学生解答数学问题要多个方向进行思考，以此来锻炼学生的发散思维能力。教学中，当学生把握题目中心后，要让学生养成“自问”的习惯，问问自己是否还有更为简捷的方法解答问题，通过促进学生运用多种方式进行问题解答，从而锻炼学生的多向思维意识和习惯。例如，若一个多边形的每一个外角都是30°，则这个多边形的边有多少条？解答此题时，教师可以引导学生从多个方向来思考求解，一方面可以从外角与其相邻的内角为互补关系、多边形内角的定义及多边形外角和的定理等方面进行解答，即设其边数为a，所列方程式为：a（180-30）=（a-2）180，当学生找到这一解题方法后，引导学生问问自己，还有别的更为简捷的解答方法吗？于是，学生发动思维，找到了单纯从多边形的外角和定理進行解答，即30a=360，教师要鼓励学生在解题过程中积极思考，锻炼发现问题本质的能力，从而准确找到最为简单有效的解题方法。课堂上，对找到不同解题方法的学生，教师要当众给予较高的评价，即便所找到的方法并不是最简捷的，也要给予积极的评价，通过长期有侧重的引导学生思维多向性，进而有效培养学生的数学发散思维，提升学生数学思维的灵活性。

二、 注重设置开放性问题，促进灵活运用

在数学教学中，教师的主要目的是培养学生的数学思想，侧重引导学生将数学思想在日常生活和问题解决中进行使用。为了推动学生数学思维的灵活性发展，在实际教学中，教师应当强化开放性问题教学，提升学生在日常学习中使用数学思想的积极性，提升学生对数学思想的理解质量和使用能力。结合教学内容所设计的数学问题应该是开放性的，答案不要局限于一个框架内，而应该对学生的发散思维进行锻炼培养，让学生从不同的角度就问题进行思考，只要符合数学规律和生活现实即应该视为正确的求解。通过有侧重地借助开放性数学问题来培养学生的数学思维，提升学生思维的灵活性。例如，已知线段AC=2AB，画出满足这一条件的图形。在针对这一题目的解答过程中，学生之间可以进行互助合作进行探究讨论，因为问题是开放性的，学生结合问题所作的思考，只要符合题给条件即为正确，通过合作探究可以有效完善答案的全面性，极大地提升学生对几何图形概念的理解和掌握质量，进而通过互助弥补来提高学生的思维灵活性和数学思维的广阔性。

三、 注重解题思想方法指导，提升思维广度

根据具体的数学问题，能够准确找到解题的总体思想方法，则可以快速对问题进行解答。初中生统筹解决数学问题的能力尚不够强，实践教学中，教师应有侧重地引导学生根据教学内容，懂得运用转化、分类、数形结合等相应的解题思想策略进行解答，拓宽学生的思维广度，从而提高解题准确率和效率。

（一）掌握转化思想的运用

初中生在数学问题的解答中常出现“局限于问题，来解答问题”的固化思维现象，以至于常受困于问题解决的无法突破。在数学学习中，转化思想可以帮助学生简化问题的结构，提升解题效率。例如，在如下数学问题的思考中，题目要求学生对图中长方形的数量进行计算。若是使用一般的计数方式，则学生可能在解题中出现思考上的疏漏。实际上，学生可以使用转化思想，借助长方形的定义来完成题目的解答。学生可以将题目中的图形进行简化，简化为包含有两个点的三条线段，将数长方形的问题转化为线段计算问题，进而快速且准确地完成题目问题的解答。

（二）懂得分类讨论思想的运用

在初中数学教学中，针对学生的数学思维不够成熟，在问题解决过程中常忽略一些实质情况的不足，教师在教学中要鼓励学生使用分类讨论思想，尽量提升问题解决过程中的全面性。将一类知识归纳分类对比，有助于学生更加深刻地理解和内化知识内涵，理顺知识间的差异，进而有效培养学生的逻辑思维，提升学生思考中的严谨性以及条理性，对学生数学能力的发展有着重要的助力作用。例如，教学“有理数大小”时，可引导学生运用分类讨论思想对一类和不同类“数”进行对比分析，如将负数与正数进行比较，负数与零、正数与零，让学生同桌间运用分类方法对比探究“数”的大小本质。同时，引导学生懂得将分类的思想方法运用于其他知识学习中，从而切实提升学生的学习能力。

（三）明确数形融合思想的运用

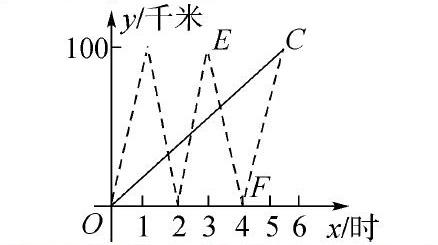
初中数学教学中，借助图形呈现严密的数量关系，可以帮助学生直观认识抽象问题，从而提升解题效率。实践教学中，运用“数”与“形”结合来锻炼学生的思维，应引导学生找准问题中所具有的“形”，从而确保能够沿着正确的方向进行解题分析，进而有效借助图形顺利解决数学问题。例如，两船同时从A港前往相距100千米的B港，甲速度为100千米/时，乙速度为20千米/小时，甲船不停往返于两港间，掉头时间忽略不计，求乙船自A港出发后直到抵达B港，与甲船一共相遇几次？学生一看便知是一道相遇问题，但若通过常规方法解题，难度较大。而基于数形结合的思想出发，来对相遇次数进行求解，可知甲、乙两船迎面相遇的路程改变，甲从后面追赶乙时，追的路程也发生改变，通过数形结合来明确乙自A→B行驶时间及路径，及甲A←→B两港之间往返的行驶时间和路程，基于此做出函数关系图，即可更为清晰地观察甲、乙两船相遇的次数，也就是函数关系图中的交点（如图所示）。通过数形结合思想的应用，切实助力了学生高效顺利解答问题。

总之，数学思维能力是学生高质、高效开展数学学习的基础，也是初中数学课程培养的重要目标。教无定法，实践教学中，教师应侧重通过培养学生优良思维习惯、设置开放性问题、注重解题思想指导等有效实施，促进学生开展高阶思维训练，从而达到有效培养和提高学生数学思维能力的教学目的，切实不断提升学生的数学综合素养。

参考文献：

[1]陈华芳.在数学教学中提升学生的解题能力[J].数学大世界，2018（8）.

[2]陈伟斌.试论初中数学教学中如何培养学生的数学思维能力[J].学周刊，2018（10）.

[3]孫彪.怎样提升数学学习能力[J].语数外学习：初中版，2018（8）.

作者简介：黄惠华，福建省三明市，福建省三明市宁化县安远初级中学。

??实际教育教学活动中，分层教学还存在很多问题，需要初中数学教师投入更多的精力和时间去研究改善，创新思维方法，推动我国教育事业的发展。

参考文献：

[1]朱锦.谈初中数学分层教学及其策略[J].甘肃教育，2020（4）：116.

[2]吴朝霞.分层教学在初中数学教学中的应用与实践[J].课程教育研究，2020（7）：145.

[3]李庚.分层教学，人人发展[J].课程教育研究，2020（6）：123.

[4]董平.核心素养下初中数学分层教学探究[J].科学咨询：科技·管理，2020（2）：221.

作者简介：官经锋，福建省南平市，福建省南平市光泽县第三中学。