时空序列模型在铁路构筑物沉降预测中的应用

陈 倜

(中国铁路设计集团有限公司,天津 300251)

近年来，随着我国铁路建设的飞速发展，铁路的安全运营日益受到人们的关注。铁路构筑物沉降监测与预测是保证铁路安全运营的重要手段[1]。目前，应用于构筑物沉降预测的方法较多，主要有神经网络模型法、灰色理论法、双曲线法、指数曲线模型法、Asaoka法、三点法、抛物线法等，以及其相应的改进方法。已有许多学者利用上述方法进行了相关研究，张文博用BP神经网络模型预测江底隧道沉降[2]；历东伟研究了双曲线法、三点法、Asaoka法和BP神经网络在高铁沉降预测上的应用[3]。然而，这些方法都是对单个时间序列进行建模预测，难以准确反映构筑物整体沉降情况[4]。

部分学者上述方法进行了优化：陈涛采用果蝇算法优化BP神经网络进行高铁路肩沉降预测[5]；谭梨基于变异粒子群改进的BP神经网络模型进行路基沉降预测[6]。这些改进神经网络模型的收敛速度或预测精度都有所提高[7]，但也都是把每个监测点当作独立的研究对象，忽略了监测点之间的空间相关性。

之后，部分学者对研究方法进行了再次改进：吉晓辉利用灰色模型预测高铁路基沉降，取得较好效果，但是预测精度尚不稳定[8]；刘文生用粒子群算法改进灰色模型，在一定程度上消除了模型本身的固有偏差[9]；胡兵提出对路基沉降序列数据进行凹化处理，提高灰色模型对数据的兼容性[10]；陈洋等用新陈代谢方法优化灰色离散Verhulst模型，并应用于基坑支护沉降预测[11-13]。这些方法以沉降监测数据的时间序列为基础，仅依据沉降数据在时间上表现出来的趋势性和相关性进行建模预测，而忽视了构筑物沉降数据内在的空间依赖性和相关性。

在铁路构筑物沉降监测时，往往需要在相应的构筑物上布设若干个监测点，然后定期测量这些监测点的沉降情况，以获取多个监测点沉降数据的时间序列，这些时间序列除了表现出时间上的趋势性和相关性外，还会表现出空间上的依赖性，在地理学第一定律中，这种空间依赖性表述为空间中任何现象或事物都是相关的，并且离得越近，这种相关性表现得越强烈。因此，在对这类构筑物进行沉降预测建模时，既要顾及其监测数据在时间上的相关性，也要顾及其监测数据在空间上的依赖性，把传统的时间序列模型向空间扩展，应用时空序列建模方法对沉降数据进行建模。目前，时空序列预测模型在多个领域都有应用研究，比较成熟的模型有时空自回归滑动平均模型(STARMA模型)和时空神经网络(STANN)模型，STARMA模型本质上是一种线性模型，在应用过程中，要求时空过程平稳[14-17]，如果时空过程为非平稳，就需要对时空过程进行特殊处理且难度较大，故以下以STANN为例进行研究。

1 时空神经网络模型

1.1 网络结构及工作原理

时空神经网络的本质就是在传统神经网络的基础上考虑时空滞，再对传统的神经元(如图1所示)进行改造，使其同时包含空间滞后算子和时间滞后算子，即可得到时空神经元(如图2所示)。

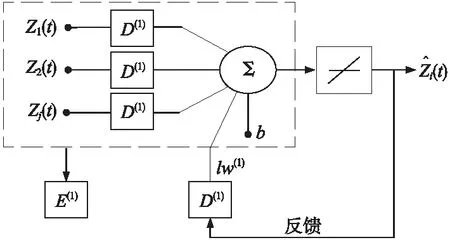
图2 时空神经元

其中，E表示空间滞后操作，D表示时间滞后操作，E(1)表示一阶空间滞后。由时空神经元构成的神经网络就是时空神经网络，为了实现对复杂地理时空数据的预测建模，需要设计出具有多个输出单元的网络结构，即时空神经网络，其基本拓扑结构如图3所示，表示由i个输出单元的3层时空神经网络。模型输入层节点的数目与需要预测的空间单元的时空滞后范围内空间单元的数目相同，隐含层节点数目可以选择与输入层节点数目相同，输出层节点的数目与需要进行预测的空间单元的数目相同。

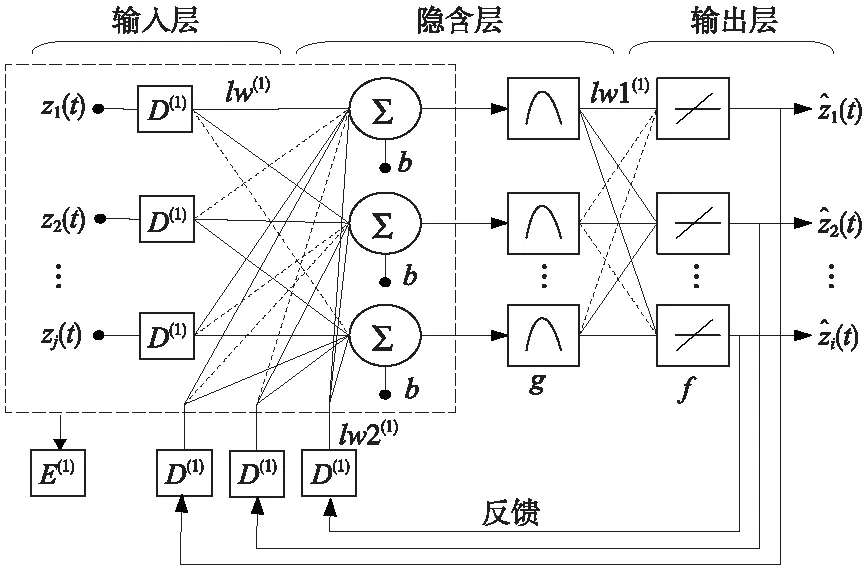
图3 i个输出单元的STANN拓扑结构

时空神经网络预测模型的数学表达形式为

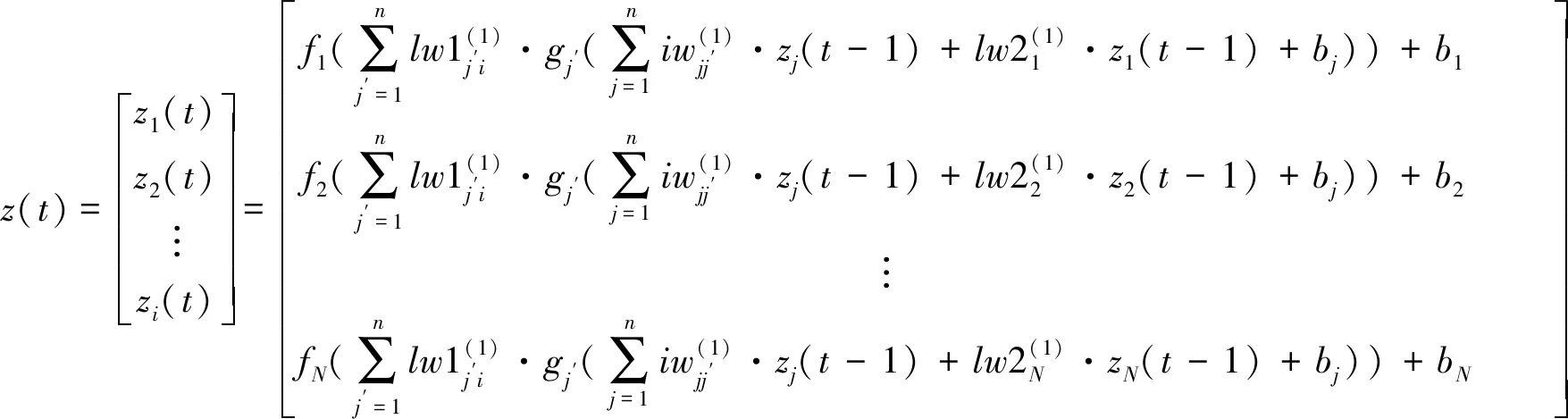
(1)

1.2 神经网络的学习方法

对于如图3所示的STANN网络，可采用反向传播算法来学习权值。STANN网络学习算法的基本数学原理为：若STANN网络第i个空间单元在训练集上的损失函数记为Δi，用最小二乘误差准则对误差进行处理，则整个STANN网络模型的总体损失函数为

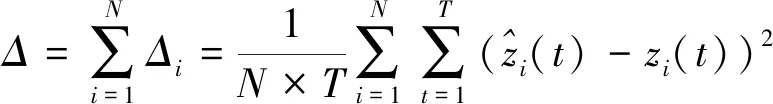
(2)

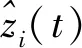
(3)

其中，gj为隐含层第j个单元的输出，则输出层的实际输出为

(4)

对于隐含层单元j的加权输入为

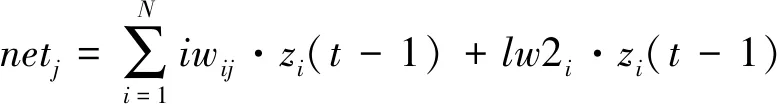
(5)

而该单元的实际输出为

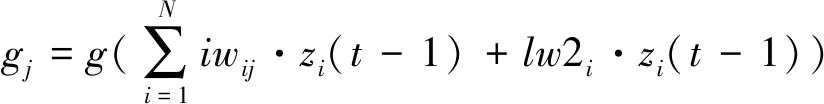
(6)

对于第i个输出层单元，其一般化误差为

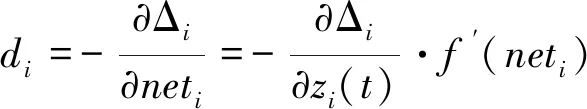
(7)

对于第j个中间隐含层单元，其一般化误差为

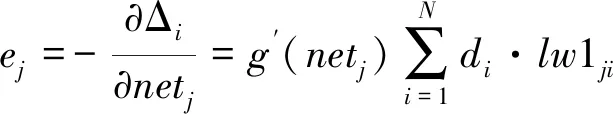
(8)

式(8)中，di(t)为前层单元的误差，它逆向传播到该层的误差为ej。

在输入层连接权iwji和隐含层连接权lw1ij的情况下，用梯度下降算法使总体损失函数减小到目标值。这时连接权系数变化计算公式分别为

(9)

Δiwij=β·ej·(zi(t-1)+lw2i·zi(t-1))

(10)

其中，α(0≤α≤1)为学习因子，β(0≤β≤1)为动量因子。

2 实例分析

以江苏省境内某铁路监测工程为例进行说明，铁路为东西走向，上跨一处3孔(3+7+3) m箱形桥。为了保障铁路安全运营，需及时掌握铁路施工对箱形桥的影响，故对该桥进行沉降监测，在桥南侧边墙和中间支撑墙上(高于地面0.5 m处)布设了6个沉降监测点，位置如图4所示。

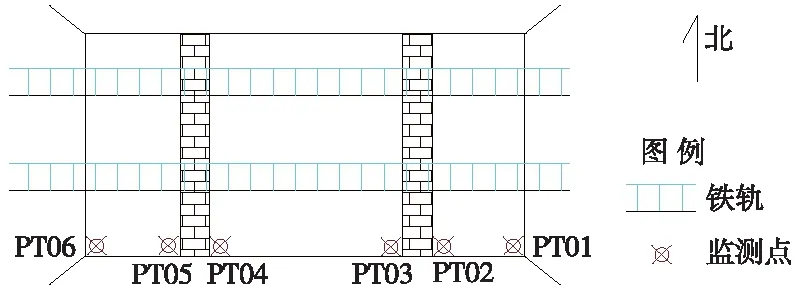
图4 箱形桥监测点位平面

沉降监测工作按照二等水准测量标准，水准线路从相同的起点开始，最后闭合到相同的终点，起点和终点按照深埋水准点的标准埋设，测量工作由固定的测量人员用相同的仪器完成，以保证测量误差最小。从2018年9月1日起，每隔5d进行一次完整监测，每次监测依次对PT01、PT02、PT03、PT04、PT05、PT06进行测量，共进行了23期。其中，前22期的累计沉降量如表1所示，6个沉降点在前期均以一定的速度沉降，在10月5日，发现监测点高程较前一期均有一定程度抬升，经过分析，认为该次抬升是由于10月5日前一周内有一次强降雨造成地基反弹的结果；10月10日，各监测点恢复正常沉降，后期各监测点沉降趋于平稳。

表1 各监测点的累计沉降量 mm

6个监测点前22期的累计沉降量曲线如图5所示，可以看到，6个监测点的沉降趋势相似度很高，进一步计算发现，6个监测点中任意两个点的沉降曲线的相关性系数都大于0.99，这说明6个点的沉降过程相似，在空间上呈现出很高的空间相关性。

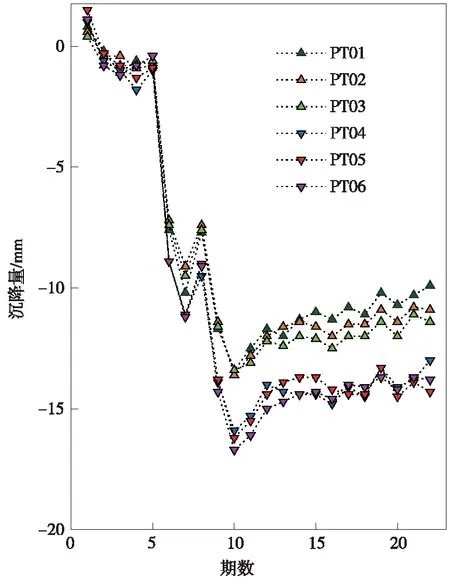
图5 各监测点累计沉降情况曲线

根据前面的描述，利用前22期沉降数据对6个监测点的沉降序列建立时空预测模型，预测第23期的累计沉降量，并用实际观测值进行交叉验证。同时，分别对6个监测点建立时间序列预测模型进行对比，选用的时间序列预测模型为比较具有代表性的灰色系统模型(GM(1，1))和BP神经网络模型(BPNN)，预测结果如图6所示。从图6中可以看出，GM(1，1)模型能预测整体的沉降趋势，但是存在一定的系统偏差，预测的沉降值均大于实际沉降值；BPNN模型能较准确地预测部分点的沉降情况(如较准确地预测了PT04、PT05和PT06这三个点测沉降情况)，但是对其他监测点的沉降量预测准确性较差(如PT03的预测值与实际观测值有较大偏差)；STANN模型能较准确预测各个监测点的沉降情况，其预测结果在空间上具有较好的稳健性。

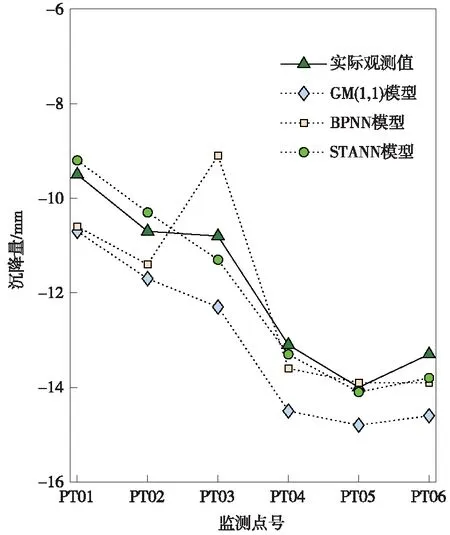
图6 第23期累计沉降量预测结果

进一步采用相对平方误差(RSE)、正态均方误差(NMSE)、均方根误差(RMSE)和绝对误差(MAE)4个误差评价指标对3种模型的预测结果进行全面定量评估，各指标的计算结果见表2。可以看到，STANN模型预测结果的各项精度评定指标都显著低于另外两种时间序列模型，从进一步而验证了时空序列模型预测性能的优越性。

表2 预测结果评估

3 结论与展望

提出把时空序列预测模型应用于铁路构筑物沉降预测，主要是考虑布设在铁路构筑物上的监测点之间具有很强空间相关性，在对其进行预测建模时，可以将同一构筑物上的所有监测点当作整体对待。实例分析表明，用时空序列预测方法对铁路构筑物沉降进行预测，预测结果的准确性和稳健性优于时间序列预测方法。但是本研究仅进行了短期预测，如何准确进行远期预测，还需要在今后的研究中加以探讨。