一类离散时延多智能体系统的安全一致性研究
2020-08-06高炎秋纪良浩于南翔
高炎秋,纪良浩,高 婷,于南翔
(1.重庆邮电大学 图像认知重庆市重点实验室,重庆 400065;2.重庆邮电大学 计算智能重庆市重点实验室,重庆 400065;3.重庆邮电大学 理学院,重庆 400065)
0 引言
近年来,一致性作为复杂系统协调控制中的基本问题,逐渐受到各领域学者的关注。多智能体系统的一致性是指在分布式控制协议(算法)下,智能体通过局部信息交互,使得系统中各个智能体的状态信息(如位置、速度和加速度等)在一定时间内趋于一致。随着多智能体系统在工程领域的广泛应用[1-3]以及多智能体系统一致性问题研究的逐步开展[4-8],多智能体系统的安全问题逐渐引起了国内外众多学者的关注[9-11]。
安全一致性问题的解决思路是对各正常智能体施加一种安全一致性算法,使其能够抵御恶意攻击,确保自身状态始终处于一定安全范围(安全区间)内,最终收敛一致[12]。为了实现安全一致性,学者们从各个方面进行了相关研究。文献[13]针对系统存在Dos 攻击,提出了一条分布式事件触发控制法则,研究结果表明,采用该控制法则后,系统能够以指数形式实现安全一致。文献[14]针对系统在遭受连接维持或连接破坏等拓扑攻击的情形,提出了一类多步分布式的算法,并给出了系统收敛的充分条件。相较以上攻击类型,文献[15]研究了系统在拜占庭攻击下的一致性问题,并给出了恶意节点数与网络拓扑连通度的关系。文献[16]针对系统存在通信时延问题,设计了一类使用局部信息的控制协议,并分析得出当正常节点的拓扑满足健壮图时实现安全一致的条件。在文献[16]的基础上,文献[12]将拓扑扩展为时变通信拓扑,即恶意节点能够改变攻击对象。除上述研究工作之外,一些学者采用迭代思想来设计安全一致性算法。文献[17]提出了有限时间内的分布式迭代学习算法。文献[18]基于上述研究,控制算法仅选取正常节点邻居信息序列的中间值作为最优信息,并以该值进行状态更新,最后给出了系统实现有限时间安全一致性的相关条件。
对于恶意节点的安全研究,有一类工作是通过算法移除极大值和极小值来降低其对状态的影响,但其还存在需进一步研究的内容,如针对较强的拓扑连通度需求,正常节点的拓扑需满足r-健壮图;算法的抗攻击能力较弱,能抵御的恶意节点数目单一;算法未进行判断而是直接选取序列中间值,增大了状态更新偏差[12, 16, 18]等。
基于上述相关研究工作,本文首先讨论了一类时延多智能体系统的安全一致性问题,并以正态曲线下距离期望值一个标准差为约束条件,设计了一种攻击容忍类安全一致性算法。该算法在处理单一恶意节点攻击时,可降低正常节点的拓扑连通度需求;拓扑连通度相同时,增强了系统抗攻击能力,即任一正常节点能抵御3 个恶意节点的攻击;对邻居时延信息进行判断,保留了若干信息值,减小了状态更新偏差和恶意节点的影响。此外,该算法还能够同时适用于固定通信拓扑和时变通信拓扑。
1 预备知识及问题描述
用G={V,ε,A}表示一个有向加权图,其中V={v1,v2, …,vn}表示图中n个节点的集合;表示图的边集合;节点的下标集合为N={1, 2, …,n};图的邻接矩阵A={aij}∈Rn×n,其中aij为节点vi与vj的连接权重。当vi可以得到vj的信息时,aij>0;否则,aij=0。定义节点vi的邻居集合为。
考虑一个由n个多智能体组成的多智能体系统,其拓扑结构可用G={V,ε,A}描述,其中每个智能体可看作图G的一个节点,智能体间的信息流可被视为图中的一条有向路径(有向边)。假设在此系统中包含no个正常节点和nm个恶意节点,Vo表示正常节点集,Vm表示恶意节点集,则有。正常节点的序号集为Wo={1, 2, …,no},恶意节点的序号集为Wm={no+1,no+2, …,n}。定义节点的正常邻居节点集合为。

如果有向图中至少存在一个节点可以沿着有向路径抵达其他任一节点,则称此图包含一有向生成树。在任意有向图中,对于图中的每个节点,若满足节点的出度等于入度,则称该图为有向平衡图。令S表示节点集为V的有向图的集合,ε(G)为图G的边集合,A(G)为图G的权重邻接矩阵,则记为S的并图。若S的并图包含生成树,则称该图集合联合包含生成树。
为了方便论述,下面先给出一些相关的定义与引理。
定义1K正则有向图[19]
对于有向图G,记
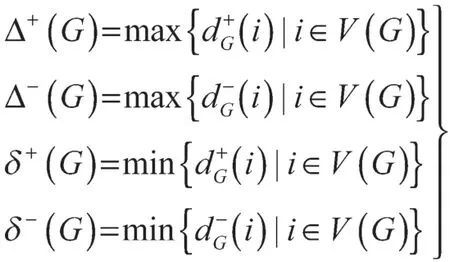
式中:Δ(G)——图G的最大顶点度;δ(G)——图G的最小顶点度。
在有向图G中,若存在关系Δ+(G)=Δ-(G)=δ+(G)=δ-(G)=K,则称G为K正则有向图。
引理1正则有向图及其生成子图至少有一棵生成树[19]。
引理2对于有向图G的Laplacian 矩阵L,0 是该矩阵一个单一特征值且1n为其对应的特征向量,当且仅当该有向图G含有一棵生成树[20]。
引理3如果存在一个列向量c∈Rn,其使得随机矩阵Q满足,则称D为SIA(系统影响评估)矩阵[21]。
引理4如果一系列有向图含有一棵生成树,则对任意序列矩阵的乘积都是SIA 矩阵,且对于每一个无限序列矩阵,存在一个列向量c∈Rn,使得[21]。
2 安全一致性算法
假设多智能体系统中正常节点满足如下动态方程:

式中:xi(t)——状态输入,xi(t)∈Rz;ui(t)——控制输入,ui(t)∈Rz。
为了论述的方便且又不失一般性,文中假设z=1。
由文献[22-23]可知,攻击类型中拜占庭攻击的破坏力最强,该类攻击节点不受约束,向邻居节点发送干扰值影响其状态更新,使系统状态偏离安全域且无法达成一致。下面先给出相关的定义。
定义2恶意节点[23]
节点va,a∈Vm为恶意节点,其具有下列属性:
(1)状态更新方程为
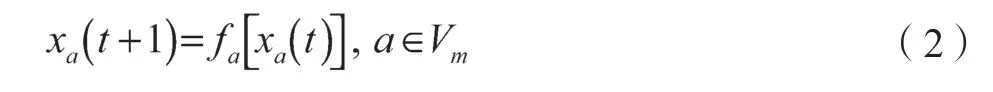
其中,fa(·)可以是任意函数。
(2)同一时刻发送不同的状态值。
(3)任意时刻可以随意改变攻击对象或者放弃攻击。
本文所考虑的恶意节点除了具有拜占庭攻击能力外,还考虑了网络中任一恶意节点之间相互共谋的能力,即在t时刻至少有两个恶意节点同时攻击某一正常节点,以及恶意节点之间相互可达。
定义3f-局部攻击模型[24]
多智能体系统中,若任一正常节点的邻居中有至多不超过f个恶意节点,则该拓扑被称为f-局部攻击模型。
定义4安全域[12]
在t=0 时刻,正常节点的状态最小值和最大值构成的区间被称为安全域,即[m(0),M(0)]。其中:

定义5安全一致性[12]
若多智能体系统能满足式(5)所示条件,则称式(1)所示系统能渐近实现安全一致。
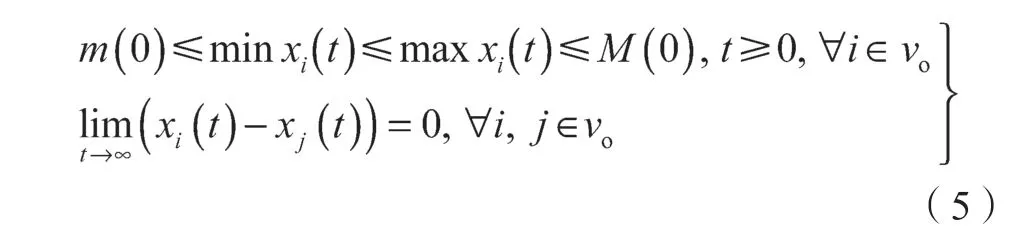
本文考虑了一种情况,即某一时刻正常节点状态值不利于状态更新而恶意节点状态值有利于状态更新,则需要判断状态值是否利于状态更新。
与文献[12]类似,本文对系统中恶意节点数目进行了限定,即系统满足f-局部攻击模型,并假设信息序列服从近似正态分布,以对状态值进行判断:x∈(μ-σ,μ+σ),符合,则保留;否则,剔除。在此前提下,所设计的安全一致性算法的具体步骤如下:
(1)对于节点vi,i∈Vo,与文献[12,18]类似,将t时刻所包含的邻居时延信息和自身信息的序列作升序排序;用安全域对其进行预处理,移除不在安全域内的恶意状态值,进而得到预处理后的新序列。
(3)记Mi(t)为步骤(2)中经约束条件处理后保留的节点集,正常节点vi所采用一致性控制协议如下:
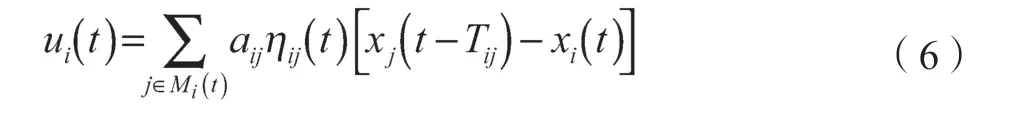
式中:Tij——节点vj到节点vi的通信时延;aij——权值,aij≥0;ηij(t)——节点通信状态值。
节点vi自身不具有输入时延。当节点vi采用节点vj的信息时,ηij(t)=1;否则,ηij(t)=0,。
3 主要结果
假设1系统中任一正常节点任意时刻被K个恶意节点攻击。
假设2系统中任一正常节点任意时刻被至多K+1个恶意节点攻击。
定理1对于时延(有界)多智能体系统式(1),其拓扑满足假设1,则在式(6)所示协议作用下,当且仅当正常节点的拓扑为1 正则有向图时,系统能够渐近实现安全一致。
证明:
(1)必要性
采用反证法。系统中正常节点构成的拓扑为1 正则有向图,则任一正常节点的邻居节点中有且仅有一个正常节点。假设系统已经收敛至一致状态z,此时恶意节点的状态值为且a≠z;对系统中某时刻入度不为1 的正常节点发送该值,此时安全算法未能将该恶意值剔除,则该值将被用于状态更新,从而打破了一致性,使系统状态无法保持一致。
(2)充分性
经第2 节中算法步骤(1)处理后,记t时刻序列的第一个数值为m′(t),最后一个数值为M′(t),显然。记约束条件保留的状态值为xj(t),j∈Mi(t),则该值始终在安全域内,即,这保证了系统的安全性。
根据式(1)和式(6),系统的闭环形式为
圆圈图适用于描述物质、化学现象和概念 初中化学教师讲解某种物质、化学现象、概念的时候,需要对其相关细节或特征进行介绍,这些细节或特征并不都是物质固有的属性,或经过反应所得,或需要在某些条件下才成立,涉及的知识比较零散。如果学生对其仅进行机械记忆学习,很容易遗忘,这时教师可用上圆圈图配合讲解。圆圈图有两个圈,小圈里可填写主题,大圈里可填写与这个主题相关的细节特征。如描述金属铁在氧气中燃烧的化学现象,小圈内写铁在氧气中燃烧作为主题,大圈内可写在空气中很难燃烧、在氧气中剧烈燃烧且火星四射、放出大量热、生成黑色固体。
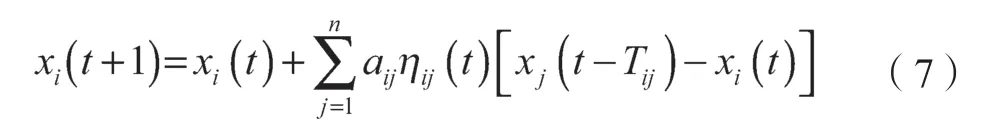
将式(7)写成矩阵形式:

用G′表示G,通过算法移除相应边后的时延图,矩阵Q(t)为时延图的邻接矩阵,矩阵为时延图的拉普拉斯矩阵。对于1 正则有向图,任一正常节点入度为1,即度矩阵D=I,可得是一个非负矩阵,因而Q(t)也为非负矩阵。恶意节点之间相互可达,再根据引理1,则系统有向图G包含一棵生成树;经过安全算法移除相应边后,其生成子图G也包含一棵生成树。根据引理2 可得,,。因此,Q(t)是一个随机矩阵且其特征值λ=1 是一个单根。根据引理3,有一个列向量c∈Rn,其使得随机矩阵Q(t)满足,可以得到Q(t)为SIA 矩阵;再根据引理4,可以得到矩阵Q(t)的乘积:

将式(9)代入式(8),系统一致性状态值为xc=cx0,其中x0为系统中正常节点初始状态,满足了系统的一致性条件。
至此,证明完毕。
推论1对于式(1)所示时延(有界)多智能体系统,其拓扑若满足假设2,则在式(6)所示协议作用下,当且仅当正常节点的拓扑为2 正则有向图时,系统能够渐近实现安全一致。
由于推论1 的证明过程与定理1 的类似,故在此处省略。
需要说明的是,对于1—局部攻击模型,采用本文算法会降低拓扑连通度要求。对于3—局部攻击模型,文献[12]算法失效,而本文算法能够实现安全一致性,增强了系统抗攻击的能力。相较文献[18],本文算法对节点的各邻居时延信息都进行了判断,减小了状态更新偏差。
4 仿真
为了验证所设计的算法是否能降低正常节点拓路连通度的需求并增强系统的抗攻击能力,分别采用满足1—局部攻击模型的系统拓扑和满足3—局部攻击模型的系统拓扑进行仿真实验。
4.1 实验1
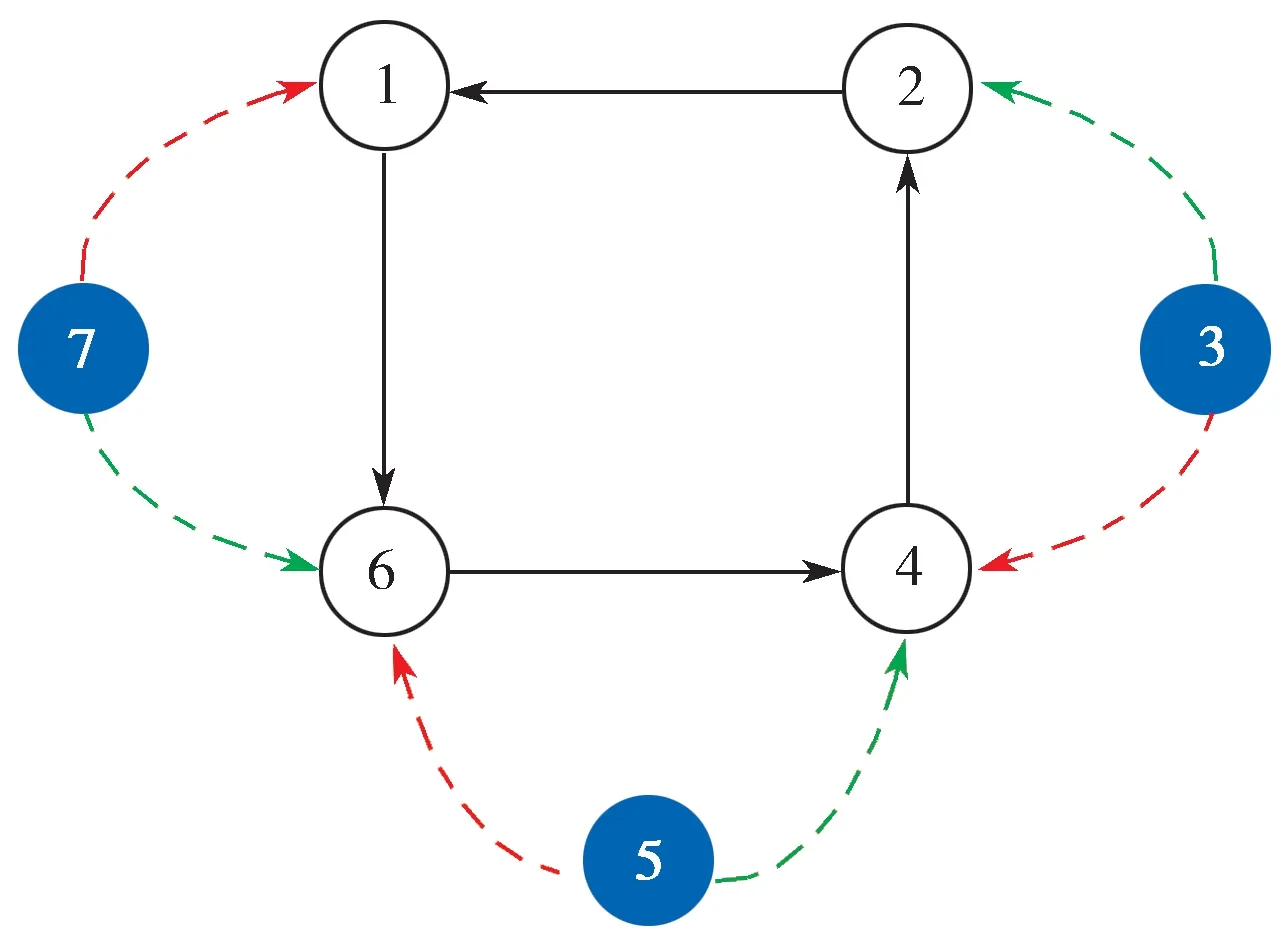
图1 多智能体系统拓扑1Fig.1 Topological structure 1 for multi-agent-system
取通信步长为0.1 s,时延上界为0.5 s。为了方便分析,此处假设系统奇数时刻和偶数时刻的邻接矩阵分别为

不失一般性,假设系统中正常节点初始状态值为x1(0)=1,x2(0)=2,x4(0)=4,x6(0)=6,恶意节点初始状态值为x3(0)=3,x5(0)=5,x7(0)=7,则恶意节点v3,v5,v7的动态方程分别为x3(t+1)=0.8x3(t)+1.4,x5(t+1)=1.5sin(0.3t)+4,x7(t+1)=1.5cos(0.3t)+3。
图1 所示通信拓扑中,任一正常节点在任意时刻会被至多1 个恶意节点攻击。根据定理1 可知,多智能体系统能够实现安全一致。各节点状态演化曲线如图2所示。
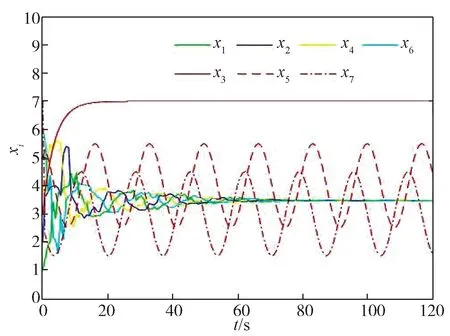
图2 1 正则有向图下的状态演化轨迹Fig.2 State trajectories under 1 regular digraph
针对图1 所示通信拓扑,采用文献[12]中的安全算法,算法容忍性较弱,无法移除部分恶意节点状态值,保留的恶意状态值成功地干扰了正常节点的状态更新,使多智能体系统状态无法收敛一致,各节点状态演化曲线如图3 所示。
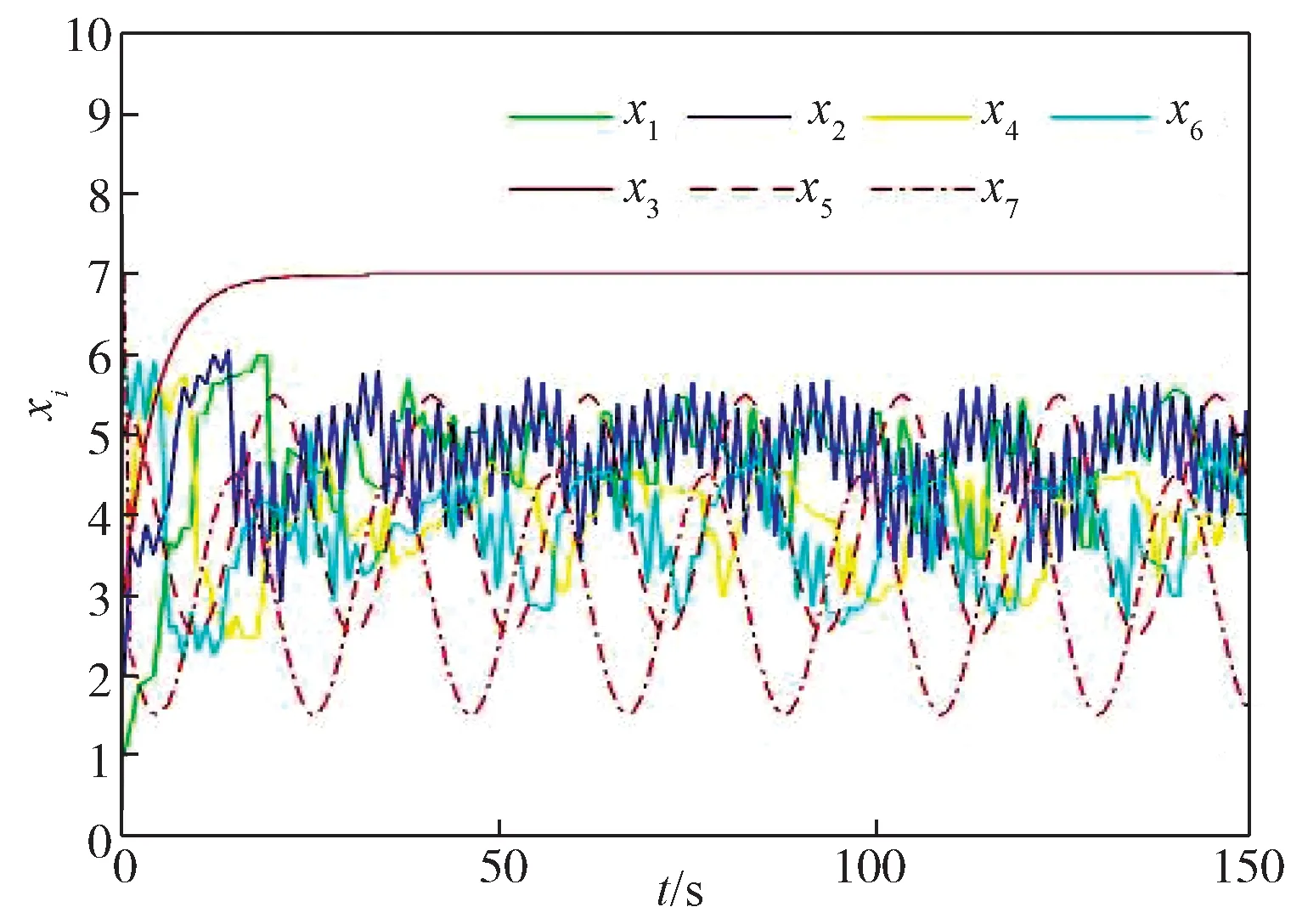
图3 文献[12]算法下的状态演化轨迹Fig.3 State trajectories under the algorithm of literature [12]
4.2 实验2
本实验将验证推论2 的正确性。假设多智能体系统包含12 个节点(4 个正常节点和8 个恶意节点),红色连接虚线为奇数时刻节点间输入边,绿色连接虚线为偶数时刻节点间输入边,实线为恒定输入边。通信步长设为0.1 s,时延上界取0.5 s,其连接拓扑如图4 所示。
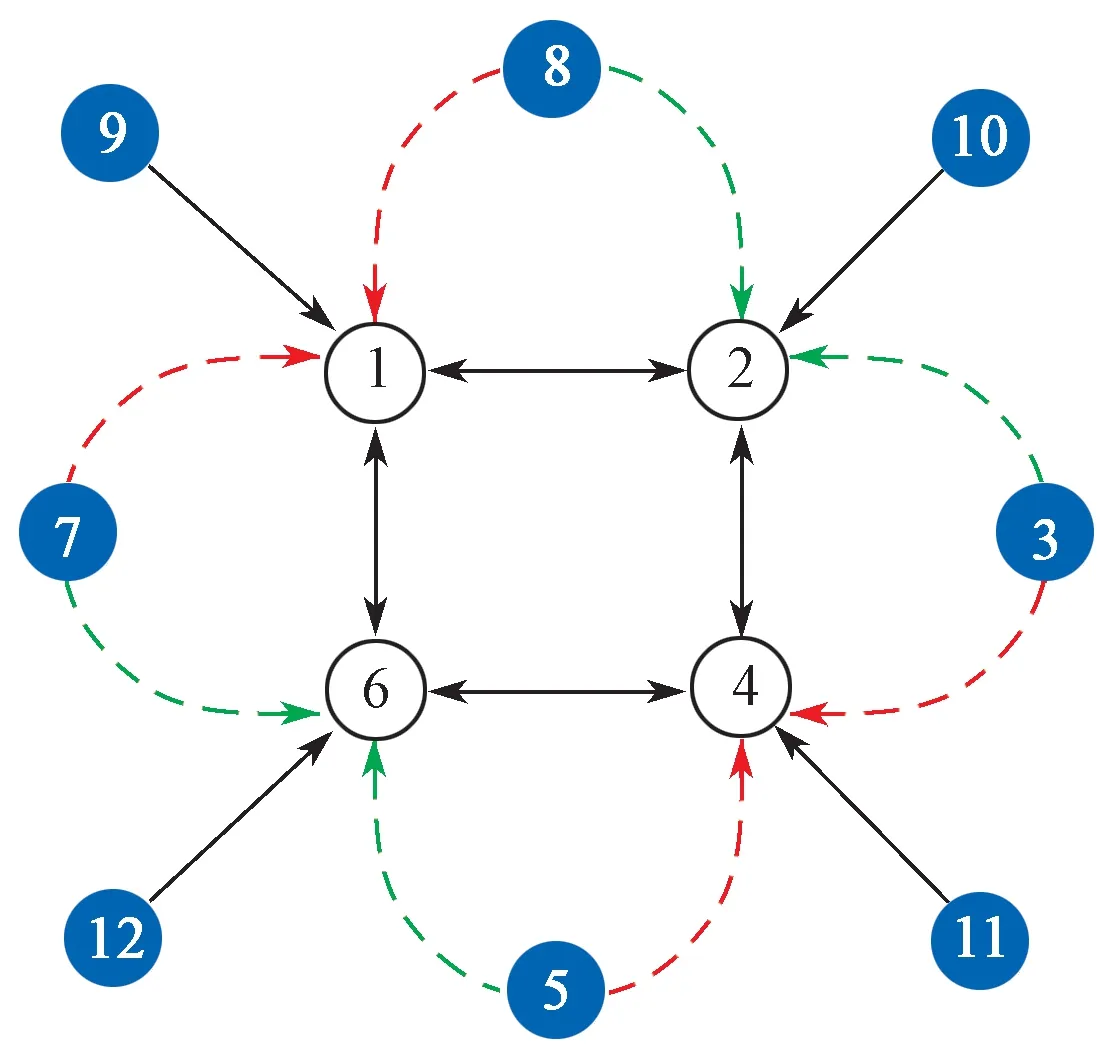
图4 多智能体系统拓扑2Fig.4 Topological structure 2 for multi-agent system
图4 中,任一正常节点在任意时刻被至少1 个且至多3 个恶意节点攻击。假设正常节点的初始状态值分别为x1(0)=1,x2(0)=2,x4(0)=4,x6(0)=6,恶意节点的初始状态值分别为x3(0)=3,x5(0)=5,x7(0)=7,x8(0)=8,x9(0)=9,x10(0)=2.5,x11(0)=4.4,x12(0)=6.6,可以验证正常节点v1,v2,v4,v6构成的拓扑为2 正则有向图。为了检验安全算法的容忍性,增强恶意节点的隐藏力和破坏力,现将恶意节点v3,v5,v7,v8,v9,v10,v11,v12的动态方程定义为安全域内变化的动态函数,分别为x3(t+1)=1.2sin(0.4t)+4,x5(t+1)=1.2cos(0.3t)+3,x7(t+1)=1.5sin(0.3t)+3,x8(k+1)=1.5cos(0.4t)+3,x9(k+1)=2cos(0.3t)+4,x10(t+1)=2.5cos(0.3t)+3,x11(k+1)=sin(0.3t)+4,x12(t+1)=cos(0.3t)+4。
各节点状态演化曲线如图5 所示。从结果可知,多智能体系统中各正常节点在安全一致性算法的作用下,其状态值始终在安全域内变化,系统一致性不受恶意节点攻击行为的干扰,最终多智能体系统能够实现安全一致。
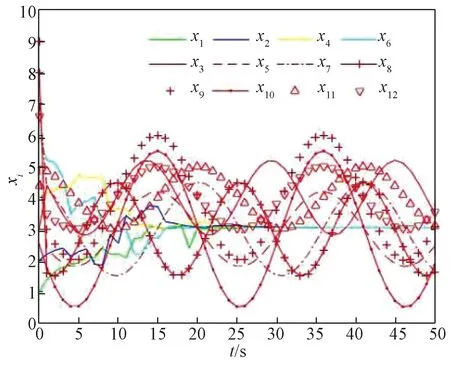
图5 2 正则有向图下的状态演化轨迹Fig.5 State trajectories under 2 regular digraph
移除图4 中节点v1到节点v2和节点v2到节点v4的输入边,这种情形不满足推论1 中的充分条件,使得系统无法实现安全一致。该条件下各节点状态演化曲线如图6 所示,此时恶意节点成功干扰了正常节点的状态更新,破坏了多智能体系统的一致性。
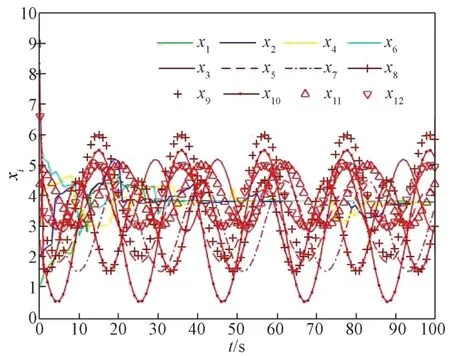
图6 非2 正则有向图下的状态演化轨迹Fig.6 State trajectories under non 2 regular digraph
综上,在实验1 中,正常节点拓扑为1 正则有向图,对比文献[12]中正常节点拓扑图,拓扑连通度降低;在实验2 中,正常节点拓扑为2 正则有向图,与文献[12]中正常节点拓扑图具有相同连通度,但每个正常节点能被3 个恶意节点攻击,增强了抗攻击能力,实验结果证明了所设计算法的有效性。
5 结语
本文研究了通信时延影响下多智能体系统的安全一致性问题,主要以拜占庭节点为恶意节点,考虑了多智能体系统的拓扑复杂度和抗攻击能力,提出了一种容忍性强的安全一致性算法。本文算法对正常节点的所有邻居信息都进行了恶意值的判断,并保留了其最优邻居节点状态集。当多智能体系统拓扑结构为时变通信拓扑、攻击模型为局部攻击模型,且正常节点的拓扑满足K正则有向图时,在安全一致性协议作用下,得出了多智能体系统实现安全一致的充要条件。仿真结果验证了该安全一致性算法的有效性和结论的正确性,该算法不仅能降低正常节点拓扑连通度需求,而且增强了多智能体系统的抗攻击能力。但是,本文研究的系统为同构系统,且节点间为合作关系,下一步我们将考虑合作-竞争关系以及异构系统。
