弹性函数的平方和指标∗

（中国电子科技集团公司第三十研究所 成都 610041）

1 引言

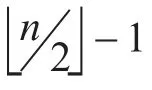
2 准备工作

首先给出相关免疫的概念。

定义1设f(x1，x2，…，xn)是一个n元布尔函数，其中x1，x2，…，xn是均匀分布的独立随机变量，如果f与x1，x2，…，xn中任意的m个变元xi1，xi2， …，xim统计独立，即对任意a1，a2，…，am和a，均有：

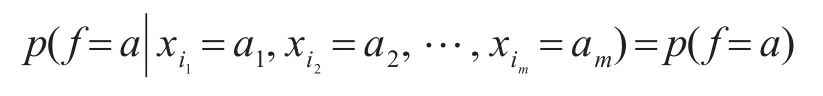
则称f是m阶相关免疫函数。

定义2平衡的m阶相关免疫函数称为m-弹性函数。

定义3f的Walsh谱为

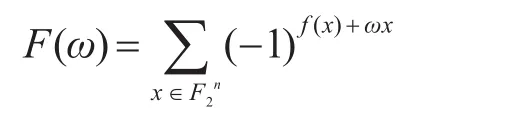
这里，ωx=ω1x1+ω2x2+…+ωnxn。

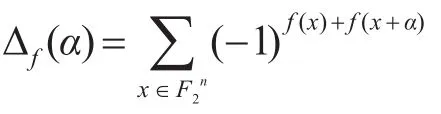
由文献［6］得以下定理。

定理1布尔函数f(x1，x2，…，xn)是m-弹性函数当且仅当对任何a∈F2n，0≤wt(a)≤m，均有F(a)=0。

由文献［1］得以下定理。

定理2设布尔函数f(x1，x2，…，xn)是m-弹性函数，这里 ，n≥3并 且m≤n-3，则F(ω)≡0(mod2m+2)对任何ω∈{0 ，1}n成立。

由文献［2］知道有下列定理。

定理3给定布尔函数f(x1，x2，…，xn)，若f是m-弹性函数（1≤m≤n-2），则degf+m≤n-1；若f是m-阶相关免疫函数（1≤m≤n-1），则degf+m≤n。

由文献［7］和文献［8］知道有下列定理。

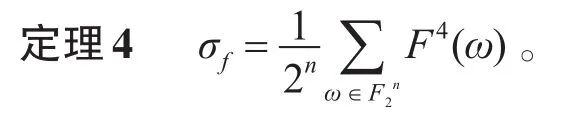
由Parseval关系有下列定理。

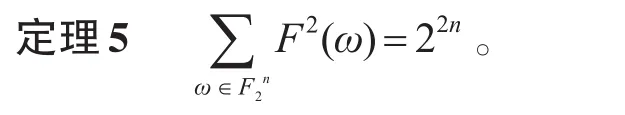
由文献［4］可得下列定理。

定理6设f是0-弹性函数（即平衡函数），则

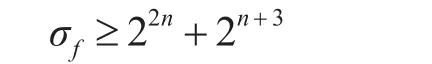
由文献［5］可得下列定理。

定理7设f(x1，x2，…，xn)是一个m-弹性函数，则

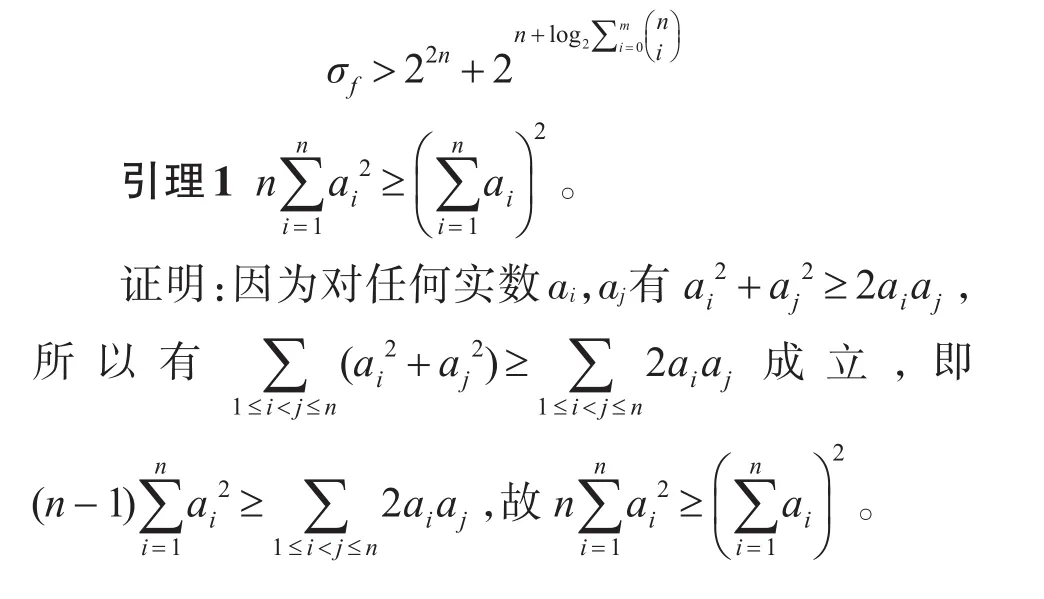
3 主要结果

这里给出并证明主要结果。

定理8设f(x1，x2，…，xn)是一个m-弹性函数，n大于或等于3且0≤m≤n-3，则

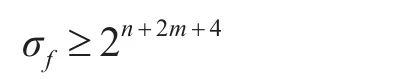
结合定理6，定理7和定理8有以下定理。

定理 9设f(x1，x2，…，xn)是一个m-弹性函数，n大于或等于3且0≤m≤n-3，则

还可以将定理9细化。

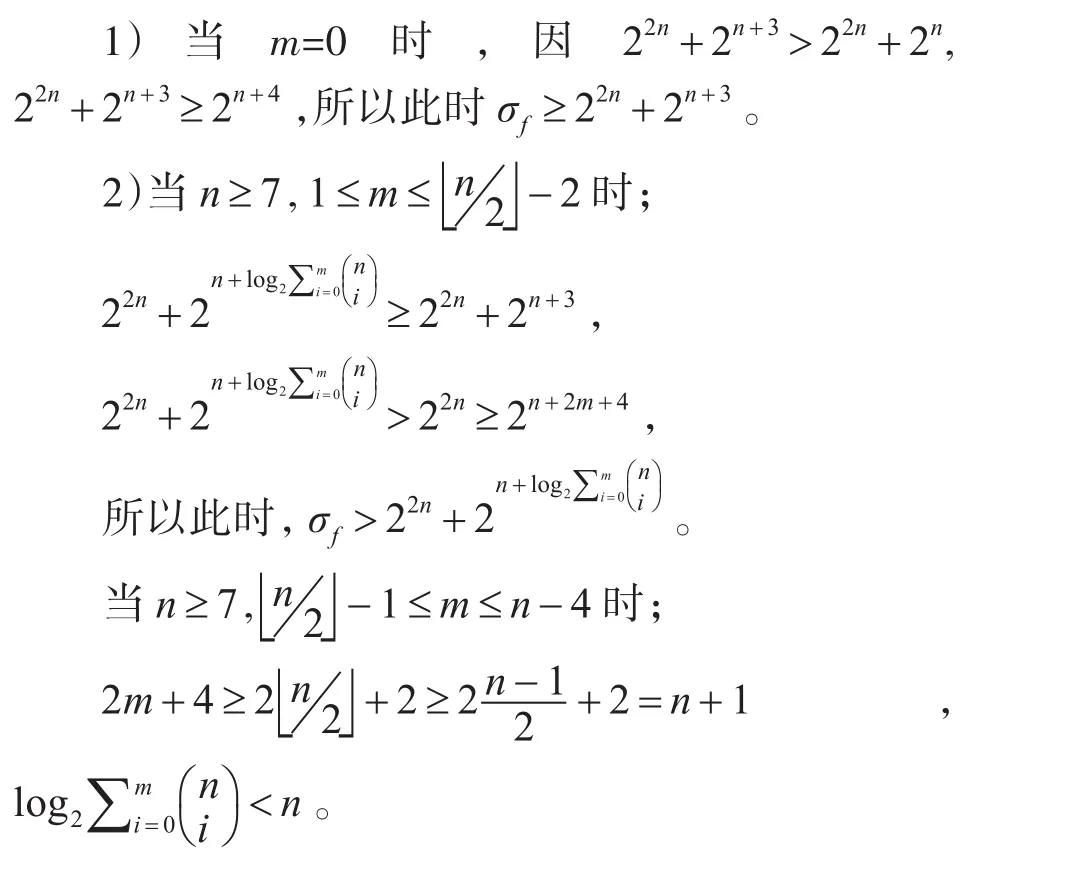
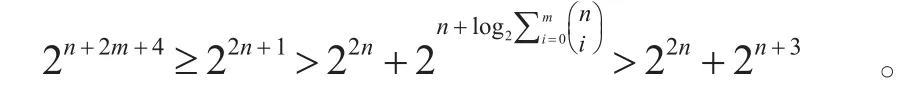
所以此时有，σf≥2n+2m+4。因此，此下界比原来给出的下界要紧一些。

3）如果f是n-3-弹性函数，则由定理2，F(ω)≡0(mod2n-1)对任何ω∈{0 ，1}n成立。由定理5，要么有4个ω满足|F(ω)|=2n-1，其余ω满足F(ω)=0；要么有1个ω满足|F(ω)|=2n，其余ω满足F(ω)=0 。由定理4，要么σf=23n-2，要 么σf=23n。

当m大于或等于n-2时，平方和指标是确定的，见下列情况。

4）当m等于n-2，n-1时，由定理3可知，f一定是仿射函数，因此一定有σf=23n。

5）考察3≤n≤6的情形。

（1）n=3；如果f是0-弹性函数且非仿射函数，由3）知σf=23n-2=27。如果f是0-弹性函数且是仿射函数。则σf=23n=29。如果f是1-弹性函数或2-弹性函数，由4）知，σf=23n=29。

（2）n=4；如果f是 0-弹性函数，由 1）知σf≥22n+2n+3=28+27=384。列举所有4元平衡函数f，发现σf≥640。因此用这个下界。如果f是1-弹性函数且非仿射函数，由3）知σf=23n-2=210。如果f是1-弹性函数且为仿射函数，则σf=23n=212，如果f是2-弹性函数或3-弹性函数，由4）知，σf=23n=212。

（3）n=5；如果f是 0-弹性函数，由1）知道，σf≥22n+2n+3=210+28。如果f是1-弹性函数，因为211=25+2+4＞210+28＞210+25+log26，所以，σf≥211。如果f是2-弹性函数且非仿射函数，由3）知σf=23n-2=213，如果f是2-弹性函数且为仿射函数，则σf=23n=215。如果f是3-弹性函数或4-弹性函数，由4）知，σf=23n=215。

（4）n=6；如果f是 0-弹性函数，由1）知道，σf≥22n+2n+3=212+29。如果f是1-弹性函数，因为212+29＞212=26+2+4，212+29＞212+26+log27，因此，这个时候，σf≥22n+2n+3=212+29。如果f是2-弹性函数，因为，26+4+4＞212+29，26+4+4＞212+26+log222，所以这个时候，σf≥214。如果f是3-弹性函数且非仿射函数，由3）知σf=23n-2=216，如果f是3-弹性函数且为仿射函数，由3）知σf=23n=218。如果f是4-弹性函数或5-弹性函数，由4）知，σf=23n=218。

上面的 1）、2）、3）、4）、5）包含了n≥3 ，0≤m≤n-1所有情况下n变元m-弹性函数的平方和指标的下界。

4 结语

布尔函数的代数免疫性质目前已有大量文献研究［9～12］。关于函数全局雪崩特征有两个指标，即平方和指标与绝对指标。这里，仅仅研究了弹性函数的平方和指标。提出弹性函数平方和指标一个新的下界，该下界可以与以前给出的下界结合起来使用。由这些下界发现：弹性函数的阶m越大，则弹性函数的平方和指标越大。但是，m很小时又要受到分别征服攻击。因此，应该选择适当大小的m，使得弹性函数的阶m较大，并且同时使得平方和指标较小。以后还应研究弹性函数的绝对指标［13～15］。可以预计，弹性函数的绝对指标并没有一个单一的下界。即对不同的弹性阶，有不同的下界（由多个公式表达）。