利用椭圆的光学性质巧解题
——例谈一道模考题的本源探究
2020-08-05陆建明
高中数学教与学 2020年11期
陆建明
(江苏省常州市第一中学,213003)
一、模考题呈现
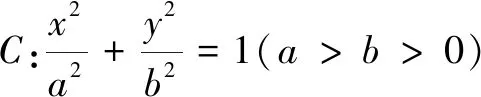
(1)求椭圆C的方程;
(2)设∆BMN是椭圆C的内接三角形.
(i)若点B为椭圆C的上顶点,原点O为∆BMN的垂心,求线段MN的长;
(ii)若原点O为∆BMN的重心,求原点O到直线MN距离的最小值.
本题为2020年江苏省南京盐城二模考试题.命题组给出的参考答案如下.

(2)(i)略.


若n≠0,此时直线MN的斜率存在.设M(x1,y1),N(x2,y2),则有
x1+x2=-m,y1+y2=-n.

6mx+8ny+3m2+4n2=0.

二、本源探究
上述解法符合解析几何的本质,用代数思想完美解决了几何最值问题.经研究,笔者发现该最值问题源于圆锥曲线的光学性质,用椭圆光学性质能够更巧妙地解决这个问题.为此,我们先证明几个相关结论.






结论3(椭圆的光学性质)从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线经过椭圆的另一个焦点,且反射镜面所在直线为椭圆在入射点处的切线.[1]
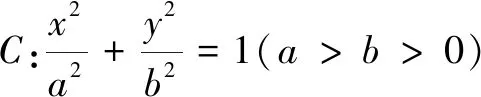
证明设∠F1AF2=α,则

三、模考题巧解
由上述本源探究,利用椭圆的光学性质,我们不难得到文首模考题的如下巧妙解答.



