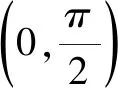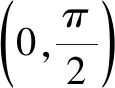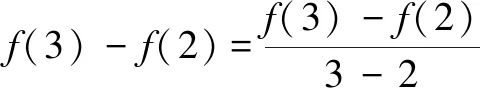欣赏几道“高观点”函数问题
2020-08-05蒋敏
蒋 敏
(四川省南充市龙门中学,637130)
在强基计划背景下,作为选拔性考试的高考数学命题更加重视对数学能力的考查.因此,将高考数学知识与高等数学知识的接轨是高考数学命题的热点. “高观点”试题是以高等数学知识(符号、概念、运算系统、公式、定理、性质、思想方法、理论、著名问题、基本结论等)为背景设计的试题,使初等数学与高等数学知识和谐衔接.既能开阔考生的视野,又能考查学生的思维能力和数学素养及潜力,在近期各地的模拟考试中备受命题者青睐.本文列举几道“高观点”函数问题进行探析,供参考.
一、高斯函数
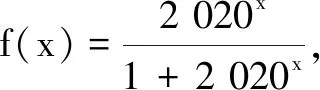
(A){-1} (B){0}
(C){-1,0} (D){-1,1}
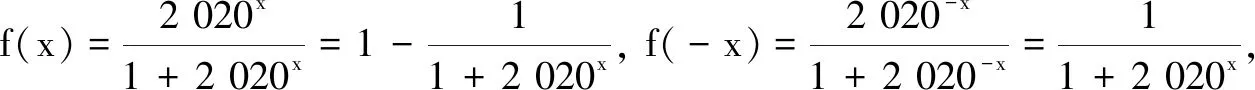
例2记[x]为不超过x的最大整数,如[0.8]=0,[3]=3.当0≤x<2π时,函数f(x)=sin([x]π+x)的最大值是______(结果可用三角函数表示(如sin 1)).
解当0≤x<1时,f(x)=sin(0+x)=sinx∈[0,sin 1).
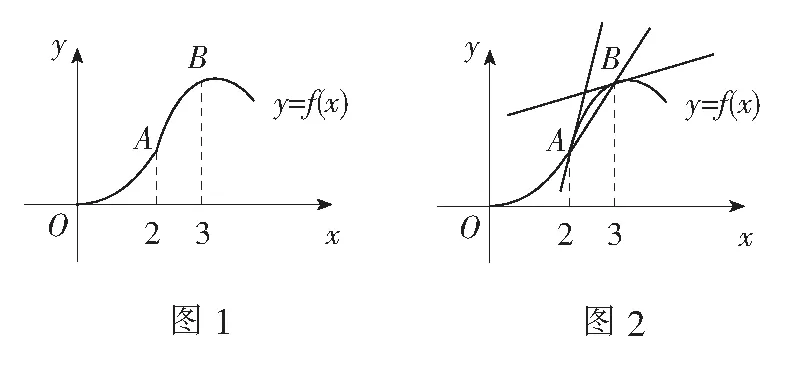
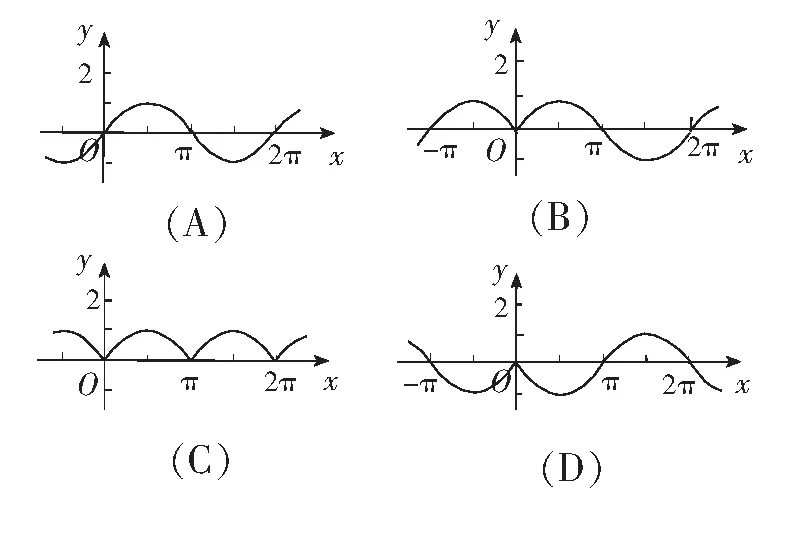
当1≤x<2时,f(x)=sin(π+x)=-sinx.注意到sin 1 同理可知,当2≤x<3时,f(x)=sin(2π+x)=sinx∈(sin 3,sin 2];当3≤x<4时,f(x)=sin(3π+x)=-sinx∈[-sin 3,-sin 4);当4≤x<5时,f(x)=sin(4π+x)=sinx∈(sin 5,sin 4];当5≤x<6时,f(x)=sin(5π+x)=-sinx∈(-sin 6,-sin 5];当6≤x<2π时,f(x)=sin(6π+x)=sinx∈[sin 6,0). 评注本题以三角函数为背景,考查了对高斯函数性质的理解和分类讨论数学思想的运用. 例3定义符号函数 则函数f(x)=sinx·sgnx的图象大致是( ) 易知f(x)是偶函数,可排除A选项;结合y=sinx(x>0)的图象,可排除C,D选项.故选B. 评注本题是以符合函数为背景,结合正弦函数的函数图象,运用排除法作出判断,考查学生综合分析处理问题的能力. (A)1 (B)2 (C)3 (D)4 解对于①,当x为有理数时,f(x)=1,f(f(x))=f(1)=1,故① 是假命题. 对于②,若x∈Q,则-x∈Q;若x∈RQ,则-x∈RQ.所以无论x是有理数还是无理数,都有f(-x)=f(x),即函数f(x)为偶函数,故② 是真命题. 对于③,当x为有理数时,x+T为有理数,满足f(x+T)=f(x)=1;当x为无理数时,x+T为无理数,满足f(x+T)=f(x)=0,故③ 是真命题. 综上,选C. 评注本题有一定的综合性,求解的关键是要明确狄利克雷函数的实质是分段函数.命题①②③从x为有理数、无理数入手,在分类探讨中使问题获解;命题④主要考查学生思维的灵活性及设计构造能力.当然,命题①也可从特殊值入手. (A)f(x)=sinx+cosx (B)f(x)=lnx-2x (C)f(x)=-x3+2x-1 (D)f(x)=-xe-x 学的结论作为条件,考查学生对新定义信息的理解与运用. 例6设f′(x)是函数f(x)的导函数,若函数y=f(x)的图象如图1,则下列数值排列顺序正确的是( ) (A)0 (B)0 (C)0 (D)0 解f′(2),f′(3)分别表示y=f(x)在x=2及x=3处的导数,其几何意义分别为经过这两点的各自切线的斜率,如图2. 所以0 评注本题的本质是考查函数的凹凸性和导数几何意义的应用.导数的几何意义是切线的斜率,反映了函数的变化率,反映函数图象上升、下降的快慢速度,即函数图象的“陡峭”程度.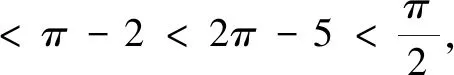
二、符号函数

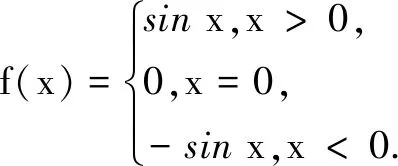
三、狄利克雷函数
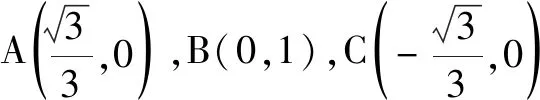
四、凹凸函数