全尾砂膏体流变学研究现状与展望（上）：概念、特性与模型

2020-08-05吴爱祥程海勇王贻明李翠平阮竹恩

工程科学学报 2020年7期

吴爱祥，李红，程海勇，王贻明，李翠平，阮竹恩

1) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083 2) 昆明理工大学国土资源工程学院，昆明 650093

金属矿产资源是国民经济和社会发展的重要支柱[1]，我国金属矿分布广泛，储量大、种类多.但是，矿产资源的持续开发导致了大量矿山固体废弃物的产生，传统采矿方法遗留的采空区和尾矿库已成为金属矿山的两大污染源和危险源.据统计，我国尾砂地表堆存量已达146亿吨[2]，地下采空区总体积达12.8亿立方米[3]，绿色安全的采矿方法成为矿产资源开发的必然选择.膏体充填技术具有采场充填不泌水、接顶好、充填质量高等特点，为地下采空区的治理和尾矿处置提供了安全、绿色、高效的解决方案，可实现“一废治两害”，从源头管控采空区和尾矿库，正逐渐成为世界各地地下金属矿开采的标准做法[4−6].随着深部资源开采战略的逐步推进，在“三高一扰动”（高地应力、高地温、高岩溶水压力及爆破、机械开挖动力扰动）特殊复杂的力学环境下，膏体充填采矿法或将成为深部资源安全、绿色开采的唯一方案.

膏体充填是将选厂排放的低浓度全尾砂料浆进行深度脱水，并与活性材料、改性材料和水搅拌均匀，制备成高浓度、流态化的膏体料浆，通过自流或泵压输送至井下采空区，实现预定充填功能的过程.膏体作为一种高固含的固液混合材料，表现出典型的非牛顿流体特性，传统的两相流理论在膏体特征描述及定量分析中表现出明显的局限性[7−9].膏体充填中浓密、搅拌、输送、充填各工艺环节均存在不同形式的流动与变形行为，膏体流变学是研究膏体的流变行为、构建数学描述及指导工程应用的有效手段.

近年来，膏体流变学得到了国内外广泛关注与深入研究，在基础科学问题上，尤其在膏体流变学概念、膏体流变特性及其影响因素、流变模型以及流变测量等方面做了大量工作，并取得了重要成果.鉴于此，本文在归纳总结国内外研究成果的基础上，概述了膏体流变学研究的必要性、特殊性及复杂性，并对多种流变模型的适用性进行了分析；归纳了膏体流变特性的关键影响因素；系统性地叙述了膏体流变测量方法及其适用性，并对测量关键问题进行了系统梳理.针对膏体流变学研究中的重点、难点及热点进行了跟踪总结，为推动膏体充填、绿色采矿以及深部开采理论与技术发展提供了战略思路.

1 膏体流变学研究概述

1.1 膏体的基本概念

膏体是多尺度散体材料与水复合而成的高浓度、饱和态、无泌水的非牛顿流体，具有不脱水、不分层、不离析的特性.受限于选矿工艺技术，全尾砂颗粒体系分布具有跨多尺度特点，从微米到毫米级.细颗粒受静电相互作用易形成稳定的悬浮体系，尤其是20 μm以下细颗粒，而粗颗粒之间机械摩擦与碰撞作用更为显著.由于膏体体系的复杂性，膏体的量化定义仍具有较大争议，国内外多认为膏体的塌落度应在 15～25 cm 之间[10−11]，屈服应力应在 100 Pa 以上[12]，20 μm 以下细颗粒占比在15%以上较为理想[13−14]；另有学者用分层度小于 2 cm[15−16]、饱和率为 101.5%～105.3% 与泌水率为1.5%～5%[17]等指标加以补充.由于膏体物料来源与组成的复杂性，在评价膏体性能时应综合考虑多因素影响.

1.2 膏体流变学研究的必要性

膏体流变学是膏体充填技术的理论基础，膏体充填的四个工艺环节均需基于料浆的流动与变形来开展.

（1）浓密阶段，需将低浓度尾砂浆（质量分数通常低于20%）经膏体浓密机深度脱水，获得稳定的高浓度底流砂浆（质量分数通常高于60%）.压缩区料浆的流变特性直接关系到耙架转速与扭矩值的设定，流变参数的分布与变化直接反映了浓密机的功效[18−20].

（2）搅拌阶段，需将高浓度底流砂浆与其他惰性材料、活性材料及改性材料等搅拌制备成均匀流态化膏体，关键在于保证膏体的均质性.理想的颗粒分散效果及活化搅拌质量与料浆所受剪切作用历程息息相关，搅拌方式及搅拌参数的确定需要考虑物料在搅拌过程中的流变行为规律，流变学特征是评估搅拌效果的关键指标[21−23].

（3）输送阶段，需将制备好的膏体料浆稳定连续地输送至地下采空区，关键在于低阻、稳定以及连续输送.膏体的满管流动调节、管道输送阻力计算、输送方式选择，以及防堵、防爆，均与料浆流变行为存在高度关联[24−25].

（4）充填阶段，需将膏体料浆充入采空区直至接顶并凝结固化，膏体在采场应具有良好的自流平效果、质量均匀、无明显的分层离析现象.膏体在采场内的流动、固结以及充填体的蠕变行为，亦与料浆流变特性演化规律息息相关[26−28].

因此，全尾砂膏体充填的整个工艺流程的需求响应均以料浆的流变行为演化为基础.

1.3 膏体流变学研究的特殊性

膏体流变学研究的特殊性主要体现在三方面：组分复杂多样、高固含及工程需求特殊.

（1）组分复杂多样.

膏体各组分的物化性质具有明显差异，体现在固体颗粒尺度、外形及表面性质等复杂多样.膏体料浆中颗粒粒径在微米至毫米级之间跨尺度分布；且受选矿工艺影响，尾砂颗粒并非规则的球形或椭球形，而呈现较大的几何外形差异；此外，不同矿山及矿山不同时期的尾砂，其化学成分差异亦十分显著，导致颗粒表面性质复杂，大量细颗粒的存在进一步加剧了化学成分差异对料浆流变特性的影响.

膏体各组分之间存在长时间的复杂相互作用，包括水化反应等.胶凝材料进行水化反应生成水化产物，或二者与尾砂组分间的化学作用，增加了膏体料浆组成体系的复杂性；此外，为改善颗粒沉降特性、料浆流动性以及充填体力学特性等而添加的改性材料，如絮凝剂、泵送剂、早强剂等，引起化学反应及微细观三维结构的改变，亦会对膏体料浆的流变特性产生影响.

（2）高固含.

膏体中固体颗粒占比高，表现出高黏性及塑性（存在显著的屈服应力）行为，流动形态为典型的非牛顿流体，具有明显的柱塞流动特点，固体颗粒分散在水介质中的两相流假设显然不适用.高固含膏体料浆中存在不可忽视的三维絮网，颗粒与水以及颗粒与颗粒之间的相互作用难以通过两相流模型中的阻力及升力等公式进行有效分析[8−9].颗粒间的摩擦碰撞效应及细颗粒间的静电作用形成的非牛顿悬浮基质流变行为，原有两相流理论很难进行解释.高固含膏体管输流动模型的建立，不能忽视颗粒的剪切诱导迁移及输送时粗颗粒径向运动规律等因素[7, 29−30].

（3）工程需求特殊.

膏体需具备不脱水、不分层、不离析的“三不”特性[17, 31].其中，不脱水指膏体中自由水含量低、内部孔隙多闭合，水分很难自由流动，在采场内泌水率极低，无明显脱水现象；不分层指垂直方向上无明显粗细颗粒分层现象，充填体固化后垂直方向上强度分布均匀；不离析指膏体料浆流入采场后，水平方向上粗骨料分布均匀，在流入口附近无粗骨料堆积现象，充填体固化后水平方向上强度分布均匀.

“三不”特性使多组分、高固含的膏体料浆进一步区别于工程中常见的固液两相流，凸显了膏体流变学研究的必要性与特殊性.此外，一些极端的工程应用环境，如热带地区与严寒地区（温度）、干旱地区与湿润地区（水分蒸发）、深部开采（三高一扰动）等，也对膏体流变学研究提出了特殊的工程需求.

1.4 膏体流变学研究的复杂性

膏体流变学研究的复杂性具体到理论研究与实验研究层面，表现为：

（1）理论研究方面.

膏体具有黏、弹、塑以及时变等特性.在不同剪切作用与剪切时间下，膏体流变行为复杂多变.研究发现，在低剪切速率下，某些膏体表现出剪切稀化特征；而在高剪切速率下，表现出剪切增稠特征[24−25, 32].膏体流变特性的复杂性，导致构建数学描述十分困难.通过建立流变本构方程来准确地描述膏体流变特性，已成为膏体充填技术发展的首要问题，也是膏体流变学的核心问题.

膏体料浆的流变行为是其微细观结构演化的宏观表现，膏体流变学基础理论的突破，离不开对微细观结构演化规律及机理的研究.由于膏体组分复杂，且具有高固含及“三不”特点，在进行理论分析时，涉及固体颗粒表征、分散介质假设、多级粒径颗粒迁移等问题，增加了膏体流变学基础理论研究的难度.

（2）实验研究方面.

由于膏体成分复杂，难以保证膏体流变测试的可重复性、测试样品成分分布的均匀性等，单次或有限数量的研究难以获得普适性结论，给膏体流变学的深度研究带来极大挑战.膏体流变特性对多种外部因素扰动敏感度高，因此，膏体流变测试对仪器及测试标准提出了很高的要求.此外，基于上述原因，在研究宏观流变行为及微细观结构演化时，单一孤立的测试与研究难以获得有说服力的结果.

2 膏体流变特性

大量实验发现，不同材料配制的膏体均表现出典型的非牛顿流体特性，但在黏性、塑性、弹性、触变性、剪切稀化及剪切增稠等特征上各有差异.

2.1 膏体的黏弹塑性

膏体的黏弹塑性特征可通过理想的应力测试曲线进行阐述，如图1所示.在控制剪切速率（CSR）模式下，剪切应力缓慢增加，膏体在初始阶段未发生流动，表现出弹性性质，应力应变呈线性关系，满足胡克定律（AB段）；剪切应力增加到某一值时，应力应变呈非线性变化，表现出黏弹性特征（BC段）；剪切应力持续增加至超过某一特定值时（C点，通常将C点作为屈服点，认为膏体于此点发生固−流转变行为），膏体发生流动，主要表现出黏性性质（CD段）.

图1 典型的膏体剪切应力−时间曲线[33]Fig.1 A typical shear stress−time curve of paste

在整个剪切过程中，通常认为在初始阶段膏体中的大量颗粒形成了具有一定刚度的网状结构，具备一定抵抗变形的能力；随着应力增加，网状结构中部分节点达到其弹性极限，开始发生断裂，膏体内部体系处于黏弹性过渡；直至网状结构完全失效，此时应力达到最大值；随后，膏体发生不可恢复且稳定的塑性流动，表现出黏塑性特征，故在稳态流动时表现为黏塑性体.

膏体充填料浆屈服前表现出黏弹性固体的特性，屈服后表现为黏塑性体的特性，膏体充填料浆在全生命周期内表现出复杂的黏塑性体特征.

2.2 膏体的剪切稀化与剪切增稠

不同的膏体料浆在不同剪切环境中往往表现出不同程度的剪切稀化和剪切增稠行为.文献[25, 34−36]发现，膏体在剪切作用下表现出剪切稀化现象，同时剪切稀化的时变特性与剪切速率存在明显的相关性.文献[24, 37]进一步研究发现，同一膏体可表现出剪切稀化或剪切增稠行为，与所受的剪切作用相关.剪切速率较低时，膏体表现出剪切稀化行为；随着剪切速率继续增加，膏体表观黏度趋于稳定，基本符合宾汉体特性；当剪切速率超过某一阈值，膏体表现出剪切增稠行为.

文献[37]认为膏体的不同流变行为与其细观结构的演变规律有关.当膏体发生剪切稀化时，颗粒间连接松散、无序；随着剪切速率增加，颗粒间的随机碰撞逐渐在流动过程中变得有序，屈服应力与黏度逐渐降低并趋于稳定；当剪切速率超过某一阈值时，强剪切促使膏体内部颗粒碰撞、粘连、聚集频度增加，作用力增强，表现出剪切增稠现象，如图2所示.

2.3 膏体的触变性

触变性是流体在剪切、振荡等机械力作用下发生的一种可逆流变行为.膏体的触变性表现为：在给定的温度等外界条件下，当受到剪切作用时，屈服应力及黏度随时间减小；当剪切作用撤去后，屈服应力及黏度随时间逐渐增大.通常认为触变行为反映了膏体细观结构的破坏与重建过程，即一定的剪切作用导致结构破坏速率大于重建速率，剪切应力及黏度降低，当剪切作用撤去，结构的重建速率大于破坏速率，剪切应力及黏度逐渐恢复[38−40].由于恢复需要一定的时间，故存在滞后性，在试验中表现为应力滞后环，即触变环.

一些分析认为[23, 41]，触变环面积可以作为判断材料触变性强弱的依据.但膏体试验研究表明，触变环分析法存在明显的局限性，触变环仅能表征剪切速率对触变性的影响，而不能有效反映时间因子的作用.如图3所示，剪切速率的峰值不同，触变环的形态尤其是下行曲线差异显著，若采用下行曲线对流变参数进行回归，触变后的塑性黏度往往大于触变前塑性黏度，这与实际情况不符.因此，触变环仅能作为材料触变性的定性判别依据，而无法定量描述触变性的大小，亦不能据此获得真实触变参数.

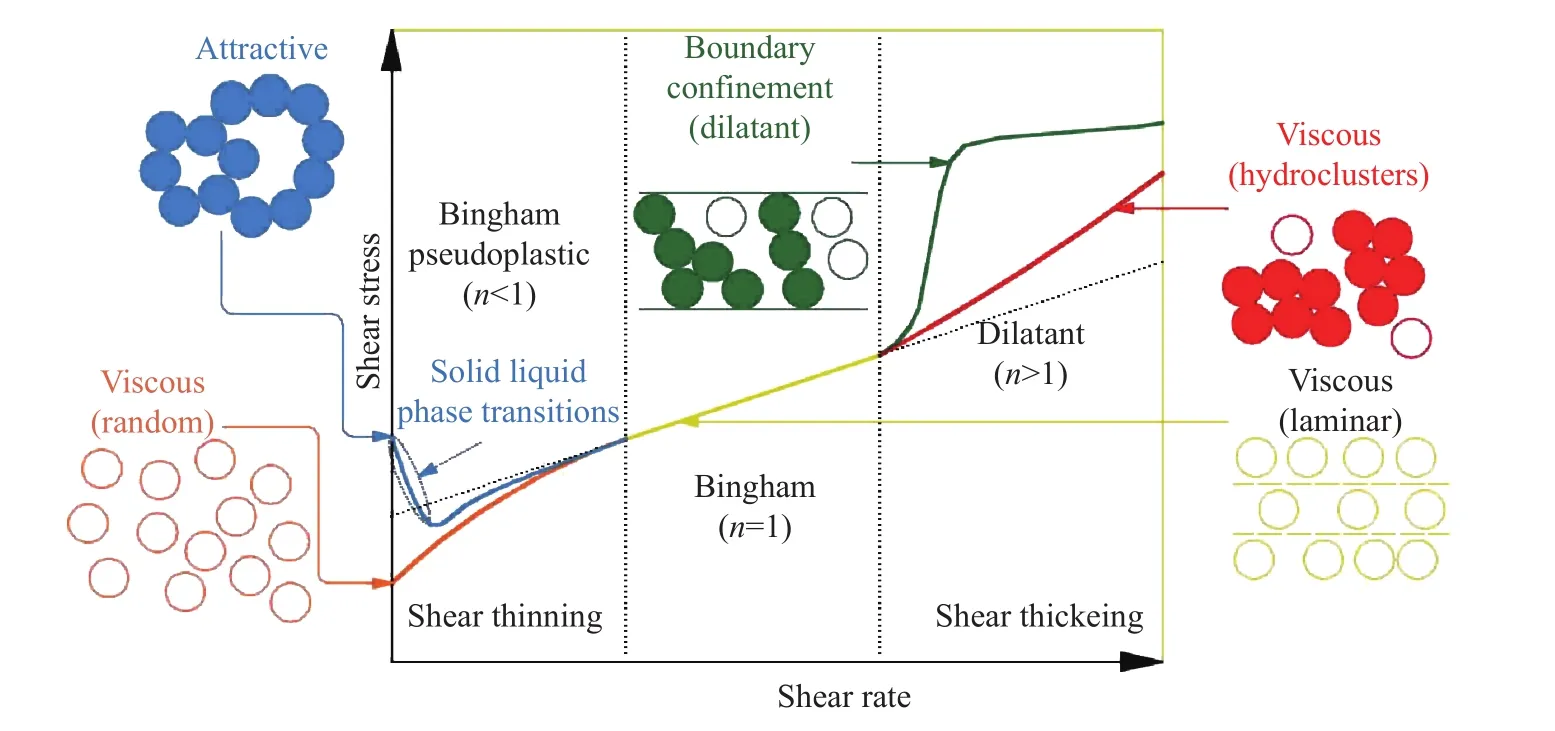
图2 不同剪切作用下膏体细观演变示意图[37]Fig.2 Changes in the microstructure of paste under different shear intensities

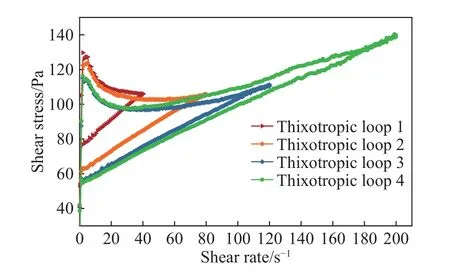
图3 触变环实验[24]Fig.3 Thixotropic loops from experiments

膏体的触变行为反映了内部结构对剪切作用及剪切时间的响应，因此膏体触变性的准确评价也需同时考虑以上两个因素.文献[24]提出了一种膏体触变性的表征方法，因发现剪切速率恒定时，膏体的应力松弛特征曲线具有规律性，如图4（a）所示，故提出可通过回归分析得到触变前后的屈服应力和塑性黏度.对应力松弛前后不同剪切速率对应的剪切应力进行拟合，如图4（b）所示，得到剪切应力随剪切速率的变化特征，进一步拟合得到触变后的屈服应力和塑性黏度.

3 膏体流变模型

3.1 非牛顿流体流变模型

（1）幂律模型：最常用的非牛顿流体本构方程之一，也称 Ostvald-de Waele公式.当n<1 时，表征剪切稀化（或伪塑性、假塑性）流体，n>1时，表征剪切增稠（或胀塑性）流体.幂律模型不适用于膏体等具有屈服应力的流体，但作为一个重要的流变模型，在屈服性非牛顿流体的数学分析中具有重要借鉴意义.

（2）Bingham模型：表征具有屈服响应的黏塑性流体的经典模型之一，描述了具有屈服应力的流体在其黏度与剪切速率无关（黏度为常数）时的流变特性.Bingham模型对膏体料浆具有较好的适用性，应用广泛[35, 46−48]，但由于模型过于简化，不能描述膏体的某些特异流动行为.

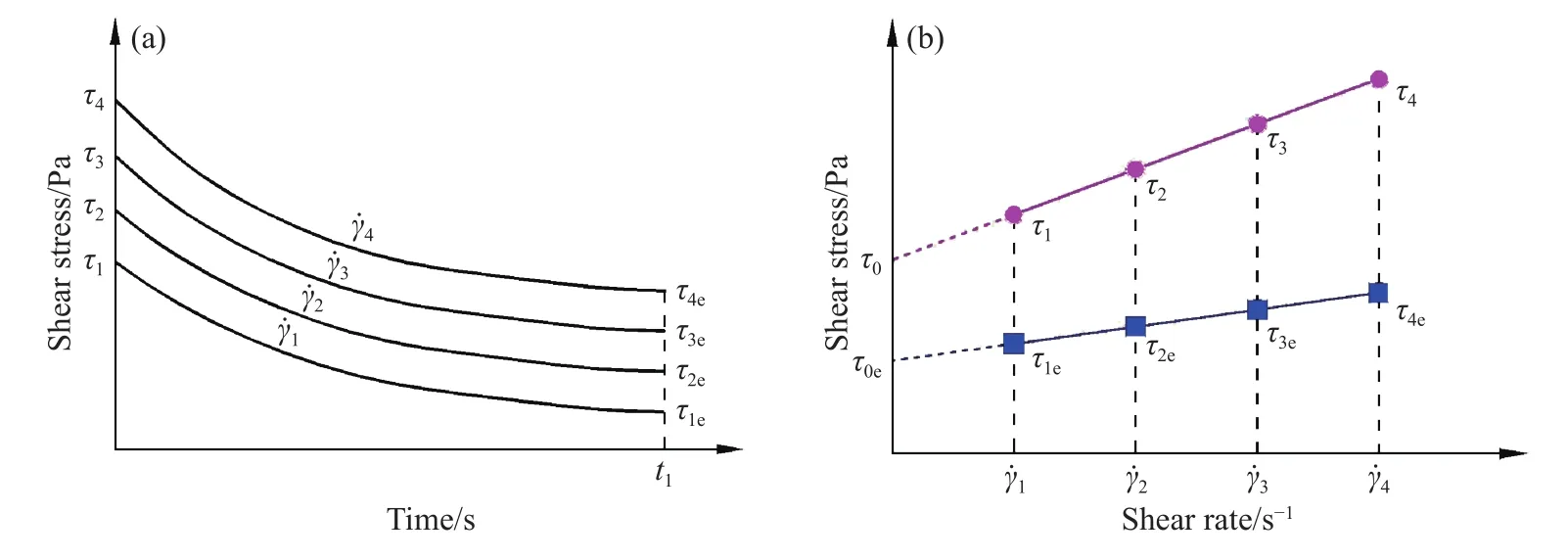
图4 触变性表征方法[24].（a）应力松弛特征曲线；（b）屈服应力回归Fig.4 A method for thixotropy characterization: (a) stress relaxation curves; (b) yield stress regression

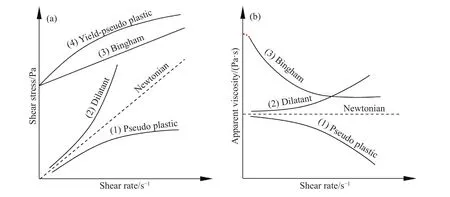
图5 常见的非牛顿体流变关系曲线.（a）剪切应力曲线；（b）表观黏度曲线Fig.5 Rheological curves of common non-Newtonian fluids: (a) shear stress curves; (b) apparent viscosity curves

表1 非牛顿流体常用流变模型Table 1 A list of non-Newtonian rheological models

（3）H-B模型：H-B模型是描述黏塑性材料屈服响应的三参数模型，可描述流体流动后剪切应力与剪切速率间的非线性关系.相比Bingham模型，能够更准确地描述膏体的流变特性[49−50]，但其水力学计算过程较为复杂，工程实操困难.

（4）Casson模型：属于半经验性模型，剪切应力与剪切速率表现为根号后的线性相关，在研究血液、生物液体等生物流变学时具有良好的适用性，在膏体中应用较少.

（5）Buckingham-Reiner公式：Bingham 流体在管道中的流动状态可划分为柱塞流动区与剪切流动区，如图6所示，Bingham流体管内流速与阻力及流体特性的关系可通过该管输流动模型进行描述.

3.2 流变模型适用性分析

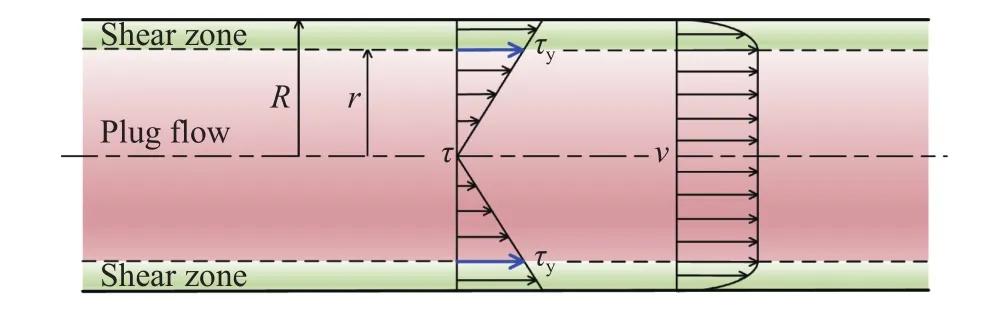
图6 Bingham 流体管道流动分区图Fig.6 Flow regimes of Bingham fluid in pipes

流变模型的适用性取决于多个因素，如拟合效果、模型简洁性、应用场景等.国内外对全尾砂膏体流变行为的研究多基于传统的黏塑性非牛顿流变模型，最为常用的Bingham模型及H-B模型具有分段函数特点，且在（）时单调递增，因此在连续性及单调性方面不足以准确描述膏体的流变特性.

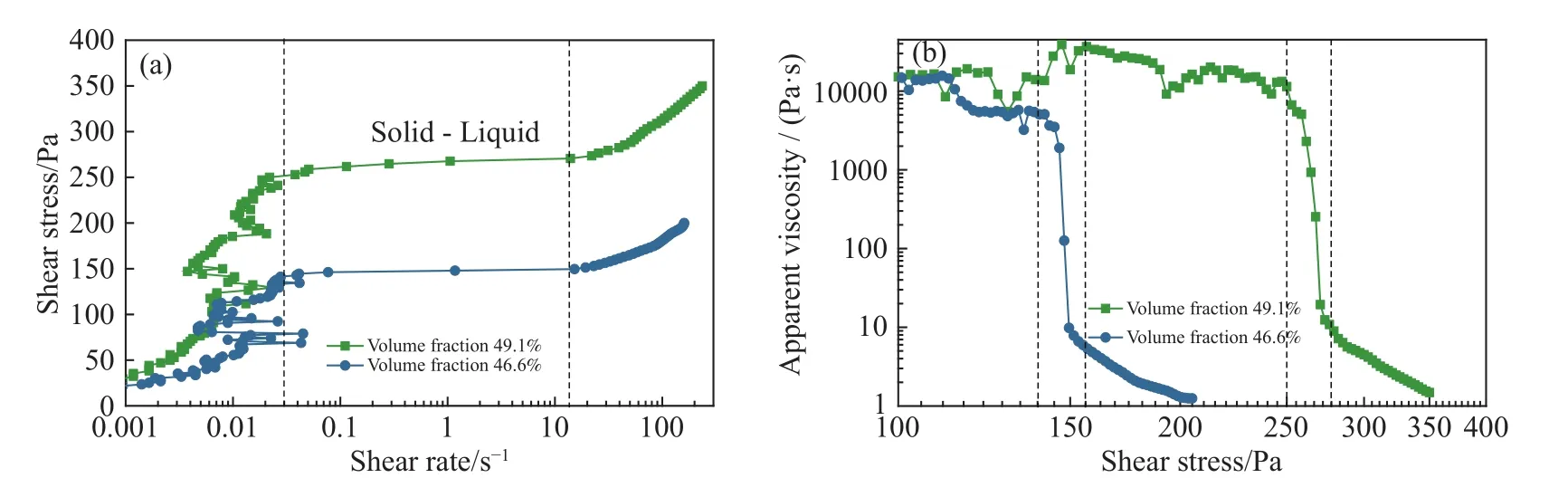
图7 膏体固态‒流态转变过程.（a）剪切应力曲线；（b）表观黏度曲线[25]Fig.7 Solid to liquid transitions of paste: (a) shear stress curves; (b) apparent viscosity curves

实验表明，膏体存在固-流转换非连续流变行为，图7分析了两种不同体积浓度膏体的流固转换现象.在较小的剪切应力值变化范围内，剪切速率突变跨越3个数量级.当剪切应力趋向于屈服应力时，剪切速率发生突变，固流转换的剪切速率并不为零.材料固流转换前的表观黏度与模型中的趋于无穷大相矛盾.

此外，一些膏体料浆在剪切速率初始增长阶段，应力过冲现象不显著，表现出典型的剪切稀化现象，而在较高剪切速率下，流体内部结构从一种有序状态变为无序状态，流动阻力增加，表现出剪切增稠.大量研究表明，在一定的剪切速率范围内（通常为 10～1000 s−1），上述模型可用于描述屈服性非牛顿流体，而在更大的剪切速率范围内，单个模型通常不足以描述流变行为.因此，Nguyen与Boger[51]建议，应当充分考虑应用场景，经验公式应与实验数据范围一致.

4 膏体流变特性影响因素

膏体的流变特性受到多种因素的影响[38]，主要包括其内部组成成分及物化性质，如固体含量、尾砂密度、固体颗粒配比和水化作用等，以及外部作用，如温度和剪切历史等.

（1）固体含量（体积与质量分数）.

固体含量是膏体流变特性最为重要的影响因素之一，通常与膏体屈服应力及黏度呈正相关关系.膏体屈服应力与其质量分数之间普遍存在（幂）指数增长关系，如回归方程式（6）[52−53]及式（7）[54]，参数取决于具体材料特性.

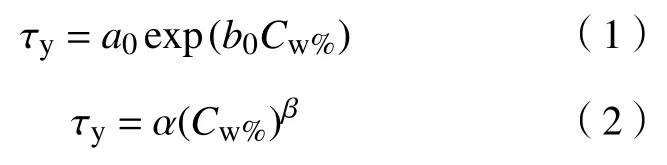
（2）尾砂密度.

由于矿物成分不同，尾砂密度存在一定的差异，对膏体流变特性将产生显著影响.膏体料浆质量分数一定时，密度大的尾砂，制成的料浆固体体积分数较低，表现为较“稀”，如含硫尾砂[55].料浆体积分数与质量分数之间的换算关系见方程式（8），图8所示为5种不同密度的尾砂制备成的料浆（胶凝材料相同）[10].

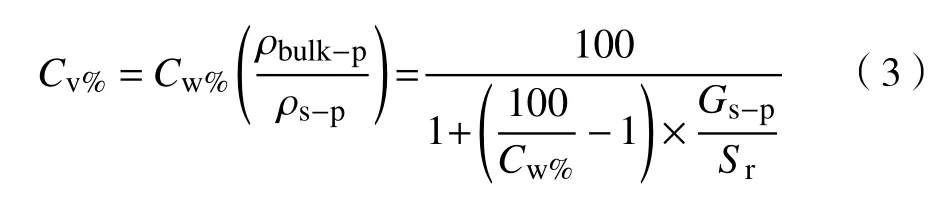
图8 料浆体积分数与质量分数关系图Fig.8 Relationship between volume fraction and mass fraction of the slurry

（3）固体颗粒级配.

颗粒级配是反映固体颗粒特性的一项综合指标，单一参数难以进行有效表征[56−57].细颗粒含量对膏体料浆的流变特性影响显著[58−59]，通常认为20 μm以下细颗粒质量分数应在15%以上，以保证膏体的流动性[13−14, 60−61].相同条件下，较细尾砂制备的料浆具有更高的屈服应力和黏度[62]，因为细颗粒的比表面积较大，颗粒间相互作用的面积增加，而粗颗粒主要通过相互碰撞和摩擦影响料浆黏度[63].改变粗细颗粒的配比，可使料浆表现出不同的流型[64].短时间内（通常 2 h 内），在动态剪切条件下，胶凝材料对膏体流变特性的影响主要表现为其粒径分布.如图9所示，水泥中20 μm以下细颗粒含量基本达60%以上，75 μm以下颗粒含量基本达100%.因此，增加水泥配比可使料浆屈服应力增大，其具体影响程度取决于全尾砂及水泥粒径分布情况[65].

（4）水化作用及温度.

膏体输送距离通常达数百至几千米，输送过程中水泥水化作用对膏体流变特性的影响不可忽视.在静置条件下，料浆屈服应力随水化作用的进行逐渐增大，但该过程受温度影响显著.实验结果表明[66−67]，料浆的屈服应力及其变化趋势在室温和低温条件下表现出显著差异，且温度不仅对料浆流变参数（屈服应力和塑性黏度）有较大影响[68−69]，对料浆的时变特性也存在一定的影响[24].

（5）剪切历史.

剪切历史指膏体在制备、输送过程中受到的剪切作用，包括剪切时间及剪切强度.具有三维絮网结构的膏体料浆，通常表现出明显的触变性，其流变特性对剪切作用非常敏感.不同的预处理状态、试验操作方法等因素都可能导致流变测试结果的差异[38, 70].不同类型的全尾砂制备的膏体，其受剪切历史的影响程度不同[71−72].在工程设计中，应充分考虑剪切历史对膏体流变特性的影响.控制剪切历史可以为优化特定应用的流变特性提供宝贵的机会[73−74].