多工况下风电齿轮箱联接螺栓疲劳寿命分析*

2020-08-05刘嘉慧林腾蛟吕和生钟建芳

机械研究与应用 2020年3期

刘嘉慧，林腾蛟，吕和生，钟建芳

(1.重庆大学机械传动国家重点实验室，重庆 400044； 2.重庆齿轮箱有限责任公司，重庆 402263)

0 引言

风电齿轮箱是风力发电机组的重要部件，所受载荷主要为风载，其载荷历程与风速、风压密切相关，受载情况复杂多变[1]。风电齿轮箱箱体一般采用高强度螺栓联接，联接螺栓疲劳失效易导致箱体渗油、漏油，引起箱体与内齿圈连接失效、传动系统断齿故障等，螺栓疲劳可靠性直接影响齿轮箱的可靠性[2]。开展风电齿轮箱高强度螺栓多工况疲劳寿命分析，对于改进齿轮箱设计、提升齿轮箱整体使用寿命具有重要意义。

为研究联接螺栓疲劳强度，已有较多经验公式和设计公式提出，如Petersen算法、VDI2230算法和Schmidt-Neuper算法等。龙凯等针对风力机塔筒法兰螺栓，基于Schmidt-Neuper理论校核螺栓疲劳强度，研究螺栓预紧力、螺栓数量与法兰厚度对疲劳损伤的影响[3]。李永奎等结合Petersen方法与VDI2230规范，建立风力机塔筒法兰与地基连接模型，计算各弹性体等效刚度，获得螺栓疲劳应力谱，分析螺栓疲劳损伤[4]。为准确计算螺栓应力和载荷分布，可以通过有限元方法实现螺栓连接部位有限元建模及应力分析。杜静等提出一种基于接触分析的高强度螺栓疲劳寿命计算方法，建立风力机塔筒和主轴的螺栓连接部件有限元模型，计算螺纹段应力及螺栓等效应力分布，并与Schmidt-Neuper算法和VDI2230算法所得理论结果进行对比验证[5-6]。Kang分别建立螺栓实体模型和梁单元简化模型，求解螺栓应力，对比得出两种模型的计算结果与理论值差异均较小，且简化模型效率较高[7]。由于风电齿轮箱结构较复杂，笔者采用有限元仿真方法，分析得到较准确的螺栓应力。

风电齿轮箱运行工况复杂，且不同工况下联接螺栓疲劳寿命不同，Liu等分析了轴向拉伸循环载荷下的螺栓疲劳性能，并基于Miner线性累积损伤理论得到不同载荷幅值和载荷比下的螺栓疲劳寿命[8]。Pennec等主要研究弯曲力矩对螺栓轴向应力及疲劳寿命的影响规律，通过计算不同螺栓位置与法兰厚度下的螺栓疲劳寿命，得出弯矩会引起螺栓轴向交变应力增大并降低疲劳寿命[9]。曹罚君针对风电齿轮箱箱体扭力臂联接螺栓疲劳强度展开研究，提出了一种径向力、轴向力及弯矩、扭矩联合作用下的螺栓应力合成及疲劳强度分析方法[10]。以上研究内容对象多为单个螺栓，少有针对风电齿轮箱整圈螺栓组分析不同疲劳工况和螺栓位置对螺栓应力及疲劳寿命的影响规律。

以风电齿轮箱联接螺栓为研究对象，采用有限元方法建立含螺栓的风电齿轮箱箱体模型，分析疲劳扭矩和弯矩工况下螺栓应力分布；根据螺栓应力结果和疲劳载荷谱，编制螺栓疲劳应力谱；基于雨流计数法和螺栓材料S-N曲线，计算单一循环应力下疲劳损伤值；进而根据线性疲劳累积损伤理论得到联接螺栓总损伤值，研究不同位置螺栓各疲劳工况下的疲劳寿命差异。

1 风电齿轮箱联接螺栓静强度分析

1.1 风电齿轮箱螺栓连接部件模型

本文研究对象为某2.5 MW风电齿轮箱，风力机轮毂中心载荷由主轴输入，经两级行星传动和一级平行轴齿轮传动，由高速轴输出。轮毂中心处载荷由各方向水平力、弯矩及扭矩共同组成，其中水平力对螺栓疲劳强度影响较小，本文主要考虑轮毂中心扭矩和弯矩影响，分析螺栓应力及疲劳损伤。

建立2.5 MW风电齿轮箱有限元网格模型如图1(a)所示，模型主要包含箱体、齿圈、主轴、一级行星架及各位置联接螺栓等，共计单元数1 207 635，节点数1 471 999。对齿轮箱各圈联接螺栓进行编号，如图1(b)所示。

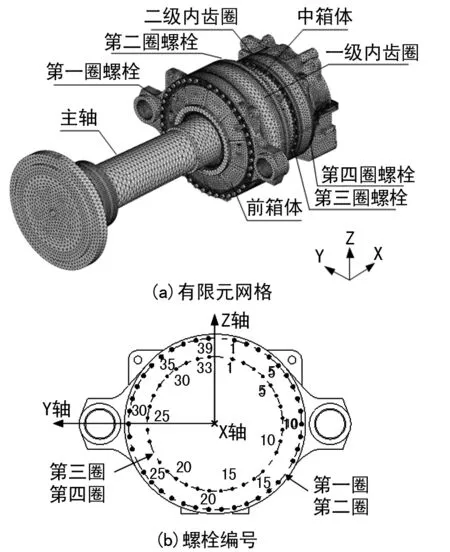
图1 风电齿轮箱有限元网格

主轴、一级行星架、箱体及齿圈采用Solid187单元划分自由网格；垫圈采用Solid185单元划分映射网格；轴承内外圈采用Solid186划分映射网格；轴承滚子用受压LINK180单元代替，近似为刚性处理。

风电齿轮箱箱体材料为QT400-18AL，弹性模量161GPa，泊松比0.274；内齿圈材料为42CrMnMo，弹性模量207 GPa，泊松比0.254；螺栓强度等级10.9级，屈服强度940 MPa，弹性模量210 GPa，泊松比0.3，螺栓参数如表1所列。

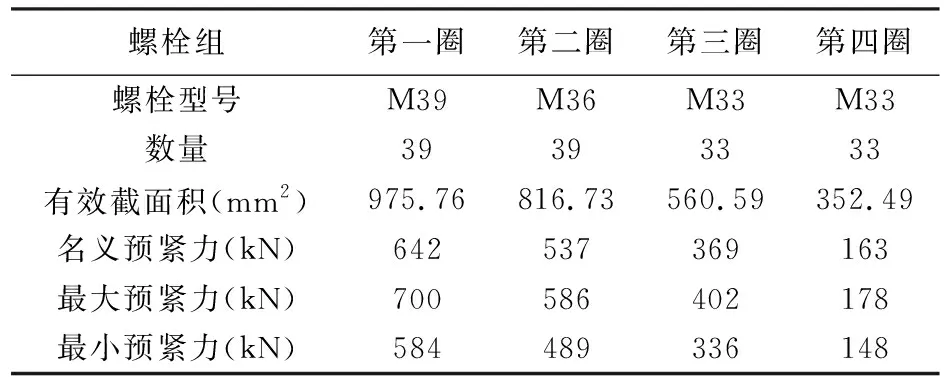
表1 螺栓参数

采用BEAM188梁单元建立螺栓模型，第一圈与第二圈为双头螺柱，螺栓梁单元模型由螺纹段与螺杆段组成；第三圈与第四圈为六角头螺栓，螺栓梁单元模型由螺母段、螺纹段与螺杆段组成；螺纹旋合区域通过刚性耦合方式连接梁单元节点与实体单元节点，模拟螺纹连接；螺栓梁单元模型如图2(a)所示。螺栓梁单元模型静强度分析可得到中心节点应力，为得到螺栓表面应力，在节点横截面一周设置16个评估点，如图2(b)所示。

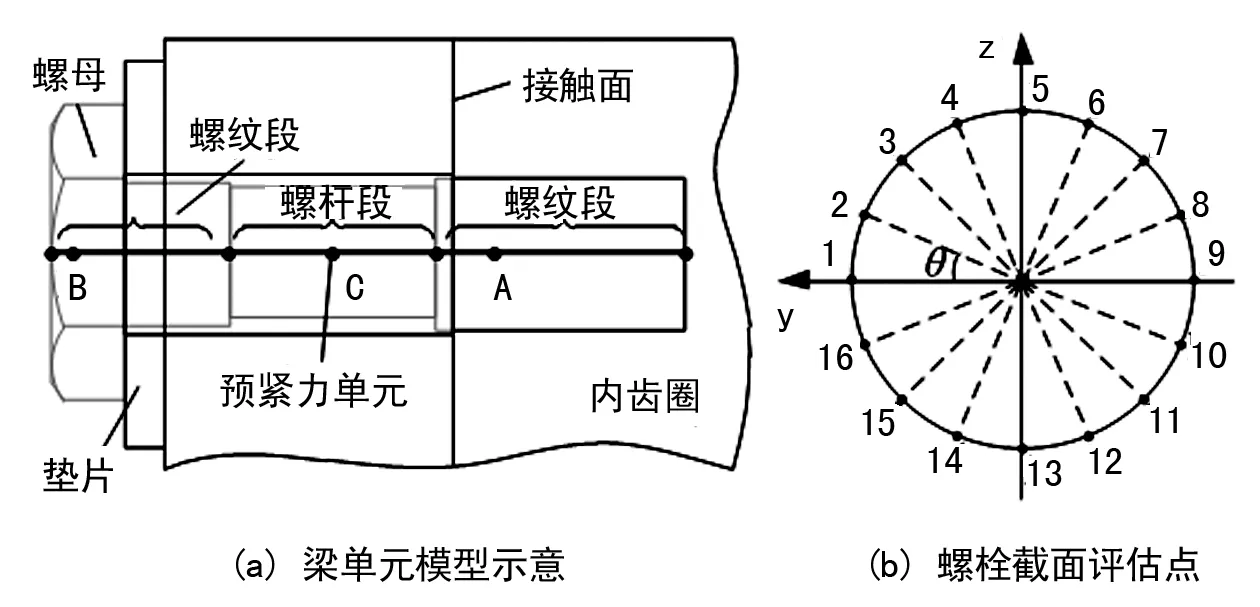
图2 螺栓模型

根据VDI2230标准计算螺栓名义预紧力FP，最大预紧力FPmax和最小预紧力FPmin如下：

FP=kReAs

(1)

FPmax=FP(1+α)

(2)

FPmax=FP(1+α)

(3)

(4)

式中：k为名义预紧力水平，取0.7；Re为螺栓屈服强度；AS为螺栓有效截面积；α为预紧力分散系数，采用液压预紧螺栓的α为0.09～0.23，考虑到文中螺栓均为长螺栓，取α为0.09。

1.2 边界条件

2.5MW风电齿轮箱支撑方式为三点支撑，在前箱体两端和主轴支撑位置添加固定约束；在各箱体及齿圈接触面间建立标准接触对，同时在销钉连接处截面建立绑定接触对，模拟圆柱销抗剪切作用；借助PRETS179单元对各螺栓施加预紧力，并针对不同工况分别在轮毂和齿圈位置施加疲劳载荷。

风电齿轮箱疲劳工况分为疲劳扭矩MX工况和疲劳弯矩MY及MZ工况。对于疲劳扭矩工况，在内齿圈中心位置建立MASS21单元，采用柔性耦合方式建立该处节点与内齿圈啮合位置节点的约束方程，并在MASS21单元上施加与轮毂中心扭矩对应的内齿圈等效中心扭矩；对于疲劳弯矩工况，在轮毂中心处建立MASS21单元，采用刚性耦合的方式建立轮毂与主轴的约束方程，并在轮毂中心节点施加疲劳弯矩，风电齿轮箱约束及载荷施加如图3所示。

图3 边界条件

内齿圈等效中心扭矩按式(5)和式(6)计算：

(5)

(6)

式中：Tpc为轮毂中心扭矩；Trg1和Trg2分别为一级内齿圈和二级内齿圈等效中心扭矩；Nrg1和Nrg2为一级内齿圈和二级内齿圈齿数；Nsun1和Nsun2为一级太阳轮和二级太阳轮齿数。

各工况轮毂中心疲劳载荷最大值和最小值如表2所列，为得到载荷与螺栓应力间的对应关系，将疲劳载荷从最小值到最大值均分为十个载荷子步加载，以得到不同载荷值对应的螺栓应力。

表2 各工况轮毂中心疲劳载荷 /(kN·m)

1.3 螺栓静应力分析

通过静力有限元分析得到各圈螺栓等效应力分布，对比各工况下螺栓等效应力可知，疲劳扭矩工况下各圈螺栓等效应力较大，给出最大疲劳扭矩工况下的螺栓等效应力如图4所示。

风电齿轮箱联接螺栓中第一圈螺栓为前箱体和一级内齿圈间的联接螺栓，靠近箱体固定端和一级行星齿轮啮合位置，螺栓等效应力较大，最大等效应力达619 MPa，单螺栓应力分布如图4(b)所示，应力较大位置位于螺纹段啮合处。

图4 扭矩工况下螺栓等效应力分布

由于风电齿轮箱联接螺栓为非受剪螺栓，其等效应力与轴向应力相差甚微，故不考虑剪切应力影响，提取螺栓梁单元节点处轴向应力及弯曲应力，按式(7)计算节点总应力σtot1。

(7)

式中：σX为螺栓节点轴向应力分量；σZ和σY为螺栓节点弯曲应力分量。

根据螺栓各节点应力计算结果，取最大节点总应力作为螺栓的总应力，各圈螺栓中第一圈及第二圈螺栓总应力较大，这里给出了各疲劳工况下第一圈螺栓应力曲线，如图5所示。

由图可知，仅预紧力工况下，第一圈螺栓主要受拉，应力在600 MPa左右，且分布较均匀。

不同扭矩工况下螺栓应力变化较大，且随扭矩增大螺栓应力增大。10号、20号、30号及39号螺栓位于行星轮与内齿圈啮合处，螺栓应力较大，同时由于10号和30号螺栓附近为箱体固定端，该处螺栓应力最大。

弯矩工况下，MY和MZ载荷造成第一圈螺栓的倾覆效应。正方向弯矩MY作用下，前箱体下侧部分受拉，上侧部分受压；负方向弯矩MY作用下，前箱体下侧部分受压而上侧部分受拉；箱体受拉时，弯矩引起的螺栓应力为拉应力，螺栓应力随弯矩增大而增大；箱体受压时，弯矩引起的螺栓应力与预紧力作用下的螺栓应力方向相反，螺栓应力随弯矩增大而减小。

MZ工况与MY工况类似，正方向弯矩MZ作用下，前箱体左侧受拉而右侧受压，27～34号螺栓应力较大；负方向弯矩MZ作用下，前箱体右侧受拉而左侧受压，7～12号螺栓应力较大。

2 螺栓疲劳寿命分析

2.1 螺栓疲劳应力谱

根据GL规范[11]，考虑正常发电、故障、启动、正常停机、暂停等疲劳设计载荷工况，借助Bladed软件计算得出符合GL规范的132个轮毂中心疲劳载荷谱，其中疲劳弯矩工况的两个疲劳载荷谱如图6所示。

图6 螺栓疲劳载荷谱

单个载荷谱长度为600 s，采样频率为20 Hz，根据轮毂中心疲劳载荷谱，结合静应力分析结果，对梁单元节点处三向应力进行转化得到螺栓疲劳应力谱。

由静力有限元计算结果可知，螺栓中心节点轴向应力在600 MPa左右，节点弯曲应力在-10～10 MPa之间且多为-1～1 MPa，螺栓主要受拉压，弯曲应力对结构应力影响较小，螺栓横截面一周的评估点结构应力σtot2计算式(7)可表示为：

σtot2=σX+σY×cosθ+σZ×sinθ

(7)

式中：θ为螺栓节点横截面一周16个评估点的位置角度。

按照表2中载荷范围施加载荷，计算各螺栓评估点结构应力值，绘制载荷-螺栓应力曲线，如图7所示为第1圈中10号螺栓第1个评估点的载荷-螺栓应力曲线。

图7 螺栓载荷-应力曲线

结合螺栓疲劳载荷谱，分段插值得到各时间点的螺栓应力，并绘制螺栓疲劳应力谱，给出图6中载荷谱对应的螺栓疲劳应力谱如图8所示。

图8 螺栓疲劳应力谱

2.2 雨流计数法

采用雨流计数法处理螺栓疲劳应力谱，该方法建立在对封闭的应力应变迟滞回线进行逐个计数的基础上，能充分反映随机加载的完整过程。借助nCode软件，运用雨流计数法可得到螺栓疲劳应力谱中各子循环应力幅值和均值对应的循环次数。

将图8中的螺栓应力谱进行雨流计数得到图9所示疲劳应力谱结果，图中长方体长、宽、高分别表示不同子循环对应的应力幅值、平均应力和循环次数。应力幅值与平均应力近似于正态分布，疲劳应力谱中循环次数较大的子循环集中分布在应力幅值较小处。

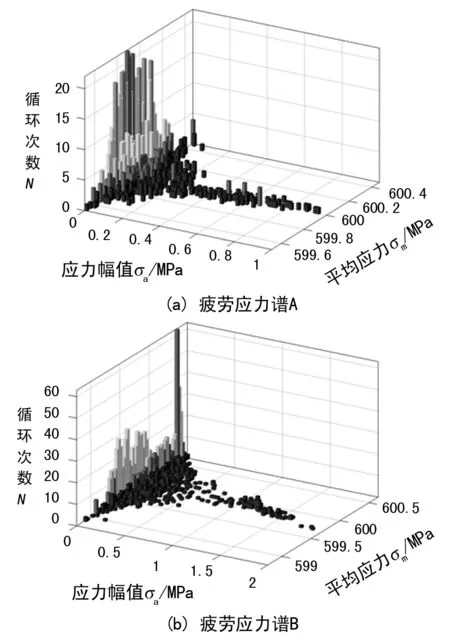
图9 雨流计数结果

2.3 螺栓S-N曲线

根据GL规范，在双对数坐标系下螺栓S-N曲线可近似为两段相连的直线。曲线斜率在拐点D点处发生变化，第一段直线斜率为-1/3，第二段直线斜率为-1/5，且拐点应力循环次数ND为5×106，拐点处应力幅值σD计算如式(8)所示。

σA为应力循环次数为2×106时的应力幅值，对于先滚压后热处理的螺栓，综合考虑螺栓安全系数和尺寸效应，σA计算如式(9)所示：

(8)

(9)

式中：γM为螺栓疲劳安全系数，取1.15；kS为名义直径d大于30 mm时的螺栓缩减系数。

以M39螺栓为例给出S-N曲线如图10所示，计算得到拐点应力幅值σD=42.6 MPa。

图10 螺栓S-N曲线

文中螺栓应力谱平均应力大于零，需考虑平均应力对螺栓疲劳寿命的影响，采用平均应力修正模型。为保证计算结果与实际较吻合，选用Goodman直线模型进行循环应力修正[12]：

(10)

式中：σa为循环应力幅值；σ-1为应力比R=-1时的疲劳极限；σm为平均应力；σb为材料极限强度。

2.4 线性疲劳累积损伤理论

在循环载荷作用下，疲劳损伤可以线性累加，各应力相互独立、互不相关，当损伤累积起来到一定数值，试件就会发生疲劳破坏。

采用等损伤线性疲劳累积损伤理论中的Palmgren-Miner理论预测变应力幅值下的疲劳损伤，应力谱中当前应力水平Si造成的损伤为Di、第j个螺栓应力谱造成的损伤Dj及螺栓评估点的总损伤值DP可按下式计算。

(11)

(12)

(13)

式中：ni为对应当前应力水平Si的实际应力循环次数；Ni为S-N曲线中对应当前应力水平Si的循环次数；Cj为第j个螺栓应力谱对应的20年循环次数；DCR为临界疲劳损伤，通常取1。

当总损伤DP大于临界疲劳损伤时，认为试件发生疲劳破坏。

结合图9、10中计算结果，按式(12)计算得到疲劳损伤如图11所示。按式(13)计算直方图中每个应力循环对应损伤值的总和，可得到单个螺栓疲劳应力谱对应的螺栓疲劳损伤值。

对比图9与图11可以看出，循环次数一定时，应力幅值较大，其子循环对应的疲劳损伤越大。

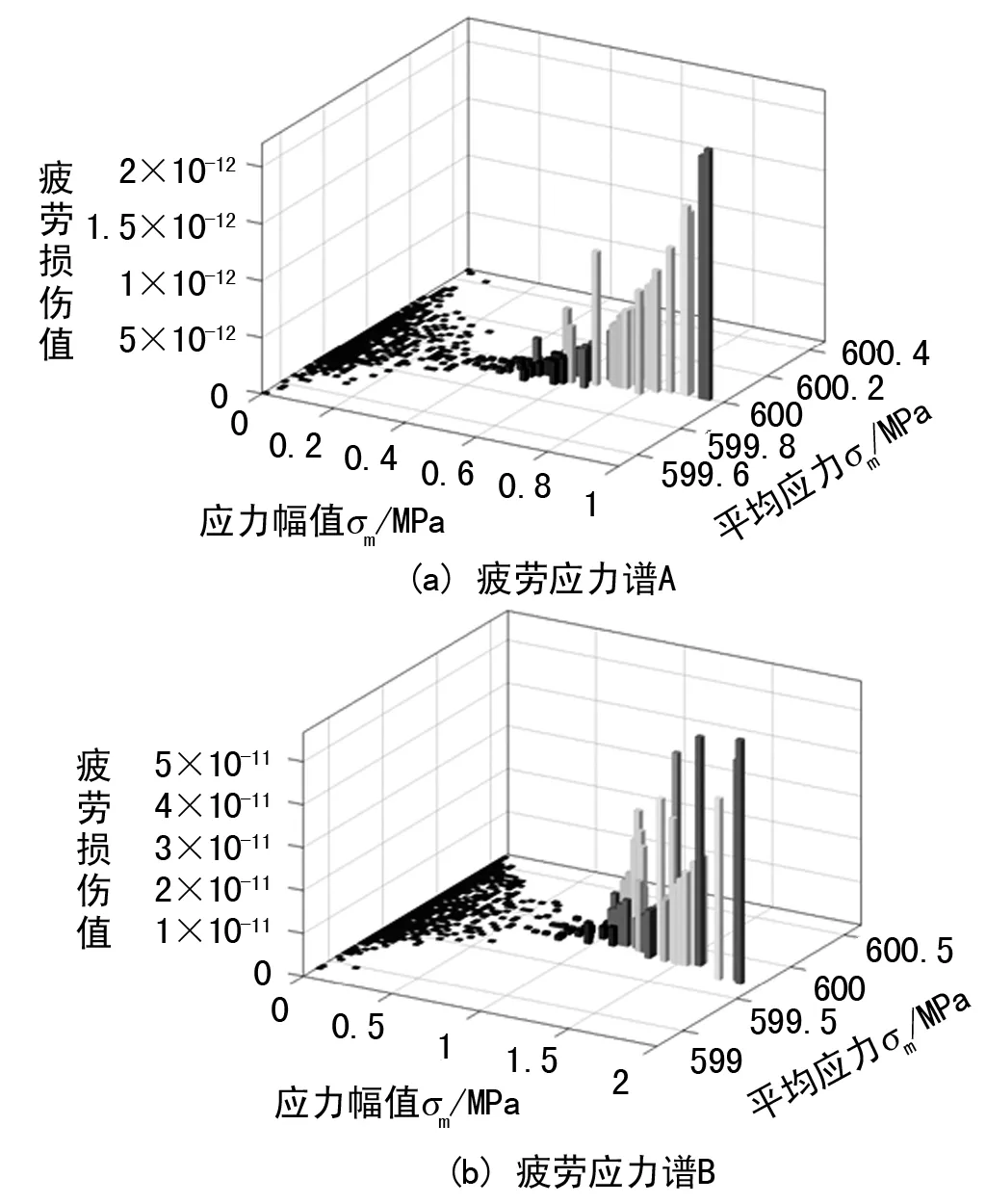
图11 疲劳损伤直方图

2.5 螺栓疲劳分析结果

将螺栓应力谱、螺栓S-N曲线输入nCode软件，设置计算类型、应力修正模型、材料表面参数等参数，计算得到各螺栓应力谱对应的疲劳损伤值，按式(14)计算各螺栓评估点的损伤值DP。

以单个螺栓各评估点中的最大损伤值作为该螺栓的疲劳损伤值，各疲劳工况下螺栓最大疲劳损伤值及对应的螺栓编号如表3所列。

表3 螺栓最大疲劳损伤值及螺栓编号

由表可知，第1圈和第2圈螺栓由于应力及应力幅值较大，疲劳损伤值也较大，第3圈螺栓疲劳损伤值次之，第四圈螺栓远离载荷施加位置，疲劳损伤值最小。最大疲劳损伤值出现在疲劳弯矩MY工况第1圈的20号螺栓上，其损伤值为0.853，疲劳寿命23.4年，可满足风电齿轮箱20年的使用寿命要求。

第一圈螺栓靠近主轴及箱体支撑位置，受载情况较复杂，各疲劳工况下疲劳损伤值均较大，疲劳寿命较低。针对该圈螺栓，给出各工况下不同位置螺栓的疲劳损伤分布如图12所示。

图12 第一圈螺栓疲劳损伤值

由图可知，不同疲劳工况中最危险螺栓的位置也有差异。疲劳扭矩MX工况下，由于靠近箱体固定端处螺栓应力变化较大，其疲劳损伤值较大，如第1圈中9～13与27～31号螺栓；疲劳弯矩MY工况下，前箱体上下两侧螺栓受到弯矩MY影响，应力变化明显，疲劳损伤值较大，如第1圈中1～7、14～27与33～39号螺栓；疲劳弯矩MZ工况下，前箱体左右两侧螺栓受弯矩MZ影响，疲劳损伤值较大，如第1圈中7～17与27～33号螺栓，且由于相应载荷谱中多受正方向弯矩，即左侧螺栓受拉，导致左侧螺栓相比右侧螺栓疲劳损伤值较大；弯矩造成风电齿轮箱前箱体螺栓疲劳寿命差异较大，产生倾覆效应，其影响不可忽略。