代数螺线在涡旋压缩机上应用分析

李冬元

广东美的暖通设备有限公司 广东顺德 528311

1 引言

涡旋压缩机是一种容积式流体机械，是被公认为技术先进的第三代压缩机。涡旋压缩机因其结构简单、体积小、重量轻、噪音低、效率高、受力平稳等优点被广泛应用在空调系统、动力工程及交通运输等领域。

涡旋压缩机型线设计是一项核心技术，其直接影响到压缩机性能及可靠性。目前，行业内多数厂家涡旋型线都是采用设计技术及加工工艺较成熟的圆渐开线形式的涡旋型线。根据目前的发展趋势可知，随着涡旋压缩机应用领域的拓展，高压缩比、大排量和高能效的涡旋压缩机研究成为涡旋机械领域的重要方向。对于圆渐开线型的涡旋，为满足高压缩比、大排量的要求，不得不靠增加涡旋齿的圈数、齿高来实现，增加了加工成本和可靠性风险。因此新型线的设计是未来涡旋压缩机研究的重点，日本日立公司香曾我部[1]1994年提出以代数螺线为基准线，采用包络法形成的变壁厚型线在小型化、高能效方面具有一定优势。2000年刘杨娟[2]对日立型线进行了详细解读及分析，并采用法向等距线方法生成涡旋型线。2003年邵兵[3]等人利用微分几何共轭曲线及法向等距线理论，证明了代数螺线作为涡旋压缩机型线的可行性。近年，相关理论研究及产品应用较少，本文通过几何推导可以更加容易地理解涡旋型线及壁厚等关键参数的含义，并通过实际产品对比得出代数螺线具有一定优势。

2 代数螺线涡旋型线的理论分析

2.1 代数螺线几何理论

在极坐标系中，代数螺旋方程为：

在直角坐标系中，代数螺线方程为：

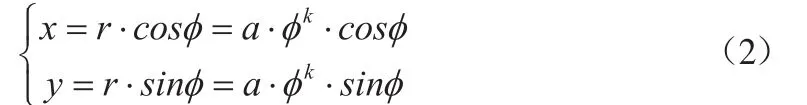
式中：

a——代数螺线系数；

k——代数螺线指数；

r——代数螺线运动半径。

图1为不同k值的代数螺线，由图可以看出代数螺线的特性，当k=1时，螺线的节距相等；当k＜1时，节距随着转角的增大逐渐减少；当k＞1时，节距随着转角的增大逐渐增大。

一对形状相同、等厚度、相位相差180°的圆渐开线型线能很好地啮合，并形成封闭压缩腔。根据啮合特性可以验证代数螺线之间不能直接啮合，当一个涡卷采用代数螺线为基准线时，可以通过包络原理[1]或法向等距线原理[2]求出对应的涡旋型线，代数螺线与其包络线、包络线与包络线之间必能啮合。因此，涡旋内外壁型线有多种选择。

2.2 代数螺线的涡旋型线

日本日立公司[1]的代数螺线包络线是以代数螺线上的点为圆心，分别在代数螺线内侧及外侧以公转半径ε作公转运动，分别在基准代数螺线内、外侧形成包络线。如图2所示。

几何关系并结合代数螺线公式（2）可知，代数螺线内外包络线方程如下：

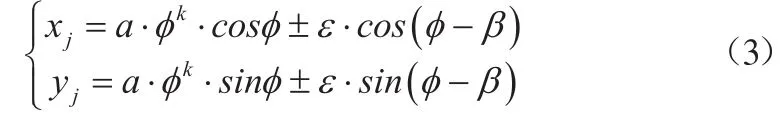
其中，未知变量β可根据几何关系式推导出如下公式：

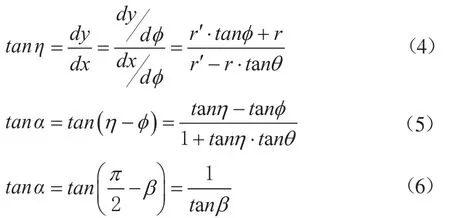
结合公式（4）、（5）、（6）可得：

公式（7）代入公式（3）可得单变量代数螺线包络线方程（8）：

此处，符号“+”为外侧包络线，符号“－”为内侧包络线。

图3为涡旋型线结构示意图，下面通过图3说明涡旋型线的构成法，图3中(a)、(b)显示了基本代数螺线以公转半径ε1和ε2进行圆运动绘制的包络线轨迹图。图3中(c)、(d)显示了动涡旋型线和静涡旋型线的构成。图3(a)实线B是基本代数螺线，虚线Bo1是曲线以公转半径ε1进行圆运动的外侧包络线，双点划线Bi1是曲线以公转半径ε2进行圆运动的内侧包络线。图3(b)实线B＇是基准线B以原点O为中心进行180°回转，双点划线Bo2是以ε2进行圆运动的外侧包络线，虚线Bi2是以ε1进行圆运动的内侧包络线。图3(c)动涡旋型线外侧曲线为Bi1，内侧曲线为Bo2。图3(d)静涡旋型线外侧曲线为Bo1，内侧曲线为Bi2，公式表示如下：

动涡旋型线方程：

外侧型线：

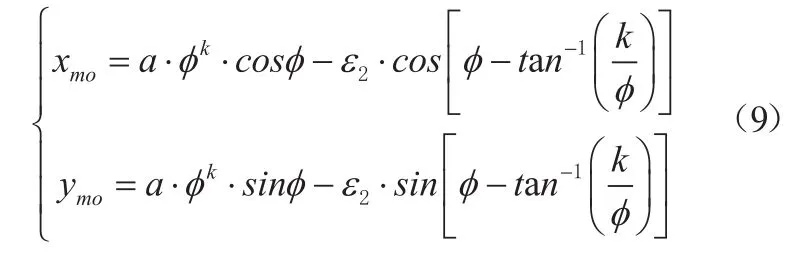
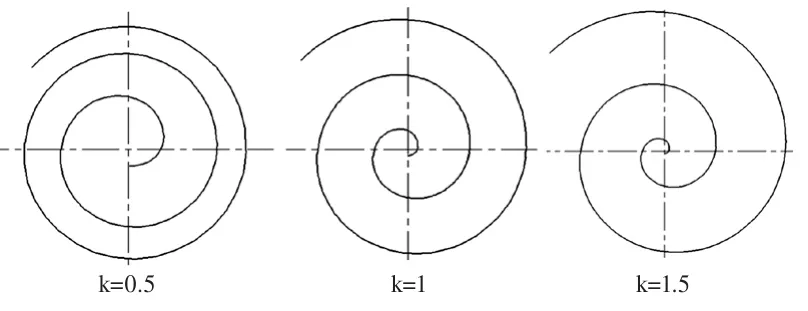
图1 不同k值的代数螺线

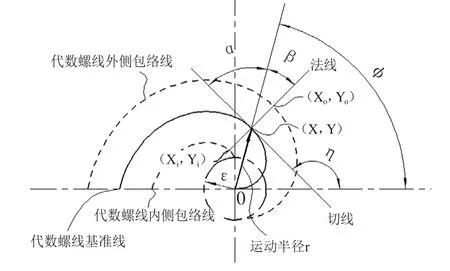
图2 代数螺线及包络线示意图

图3 涡旋型线结构示意图

图4为不同k值的代数螺线涡卷示意图，由图可以看出[4]，代数螺线涡旋压缩机的涡卷，代数螺旋指数k不同，涡卷的壁厚和节距都有变化。

图4 不同k值的代数螺线涡卷示意图

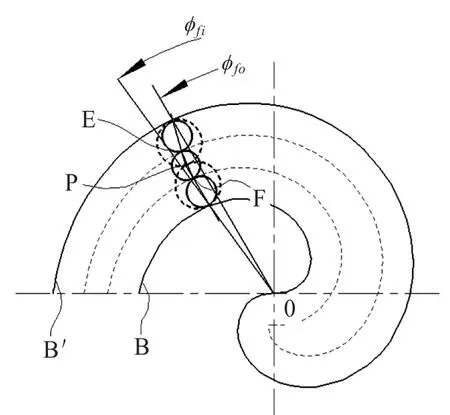
图5 壁厚t说明示意图

当k=1时，壁厚和节距都不变，形式上与圆渐开线涡旋相似；当k＜1时，涡卷壁厚和节距向外圈方向逐渐减小；当k＞1时，涡卷壁厚和节距向外圈方向逐渐增大。

涡旋压缩机在运行过程中，当涡旋型线脱离啮合点位置时，涡卷中心部承受着较大的温度及压差，此时涡旋中心部会出现强度不足的风险。但当k＜1时的代数螺线作为型线时，适当设计中心涡卷部厚度，能够获得较好的强度，可靠性将会得到提升。

此处，结合图4静涡旋型线来定义涡旋的壁厚，取公转半径ε1和ε2相等为ε。涡旋壁厚用涡旋的外侧曲线和内侧曲线间内接圆的两个接点，即接点E（Xfo，Yfo）和F之间的距离t来定义，P点为内接圆的中心（，Yc），内接圆半径用r来表示。

由几何关系可知：

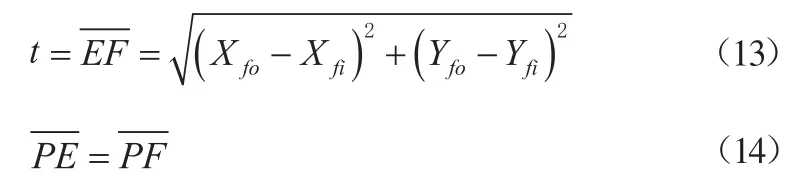
由E点（公式11）、F点（公式12）方程，以及代数螺线及包络线原理可得内接圆中心坐标方程：

其中：

通过上述公式，结合数值计算可以得出不同偏转角度下的E、F点坐标，内接圆半径r，以及壁厚t等数值。

2.3 代数螺线型线工作腔容积

代数螺线包络线与代数螺线包络线作为涡旋型线的一对涡盘啮合形成月牙形压缩腔，如图6所示，双点划线表示动涡旋内壁型线，实线表示静涡旋外壁型线。OmA、轴的正向夹角分别为啮合点A、B在基准线上对应点与Xm轴的正向夹角分别为轴的正向夹角分别为，且啮合点A、B在基准线上对应点与Xt轴的正向夹角分别为

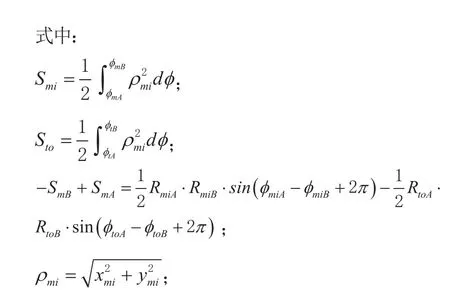
于是，第i个压缩腔的横截面积为：

第i个压缩腔的容积为：

如图7所示为指数k不同时，代数螺线的容积变化特性。图中曲线表示从吸气终了形成封闭容积后，经过压缩直至排出整个过程的容积变化。随着回转角逐渐增大，压缩腔内气体逐渐被压缩而减少容积，当回转角到达排气时，涡旋压缩机开始排气，容积不再变化。当k=1时，容积变化基本上为线性关系；当k＜1时，容积变化比k=1时要缓一些，且k值越小变化越平稳；当k＞1时，容积变化比k=1时要快，且k值越大变化越快。

3 代数螺线型线与圆渐开线型线对比

3.1 基本参数

表1和图8对排气量72 cm3/rev进行代数螺线与圆渐开线基本参数对比分析。

由表1和图8可知，在涡旋盘直径设计相同时，代数螺线设计上可以更灵活，壁厚中心部不包括修正段处的最大壁厚可达5.15 mm，涡卷结束端可达3.87 mm。同比等壁厚4 mm圆的渐开线形式强度上有很大的提升。

3.2 吸气腔面积对比

表2对代数螺线与圆渐开线型线在相同盘径情况下的吸气腔的投影面积情况进行对比，可知代数螺线涡旋吸气闭合腔A和腔B的投影面积明显大于圆渐开线型线。在相同72 cm3/rev吸气容积时，代数螺旋齿高为28.5 mm，圆渐开线为32 mm，同比齿高下降11%左右。因此，代数螺线同比圆渐开线具有更短的密封线长度，性能应有一定的提升。

3.3 气体力及力矩对比

图6 压缩腔面积示意图

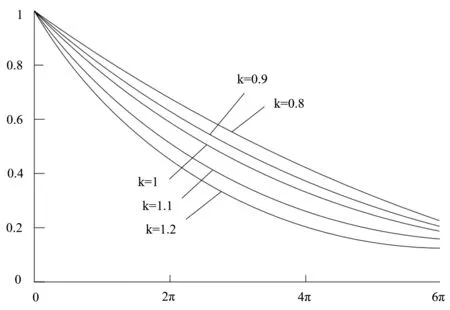
图7 压缩腔容积变化示意图

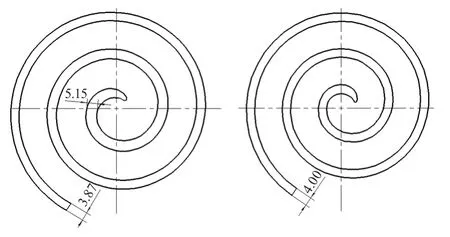
图8 代数螺线与圆渐开线涡旋壁厚对比示意图

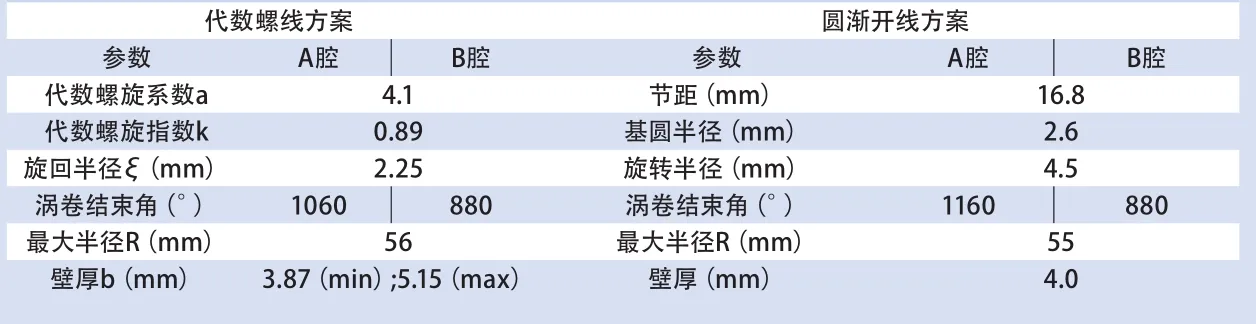
表1 代数螺线与圆渐开线参数对比

表2 代数螺线与圆渐开线投影面积对比

涡旋压缩机工作过程中主要受力形式为动静涡旋盘之间存在的气体力[5]，分为轴向力、切向力、径向力以及它们之间形成的力矩等。如何平衡气体力是涡旋压缩机行业的核心问题，设计不充分将会引起低压比工况泄漏大，高压比工况磨损过大的情况。通过代数螺线与圆渐开线方案对比可知，盘径相同、工况相同下，轴向气体力相差不大，工程应用上差别可以忽略。径向气体力相对轴向力和切向力小很多，对比可忽略。由于代数螺线齿高降低了11%左右，经过计算同比切向上所承受的气体力大约也降低了10%左右，齿高的降低会带来重心的降低，代数螺线由切向力带来的倾覆力矩也会降低。

下面通过ARI工况，对比代数螺线与圆渐开线型线切向气体力及倾覆力矩变化情况，如图9所示。

通过图9可知，代数螺线同比圆渐开线型线具有更小的倾覆力矩，这样在平衡力设计时可以减少背压力设计，在满足密封的前提下可以减少高压比等工况下的密封力，从而可以在一定程度上提升能效。

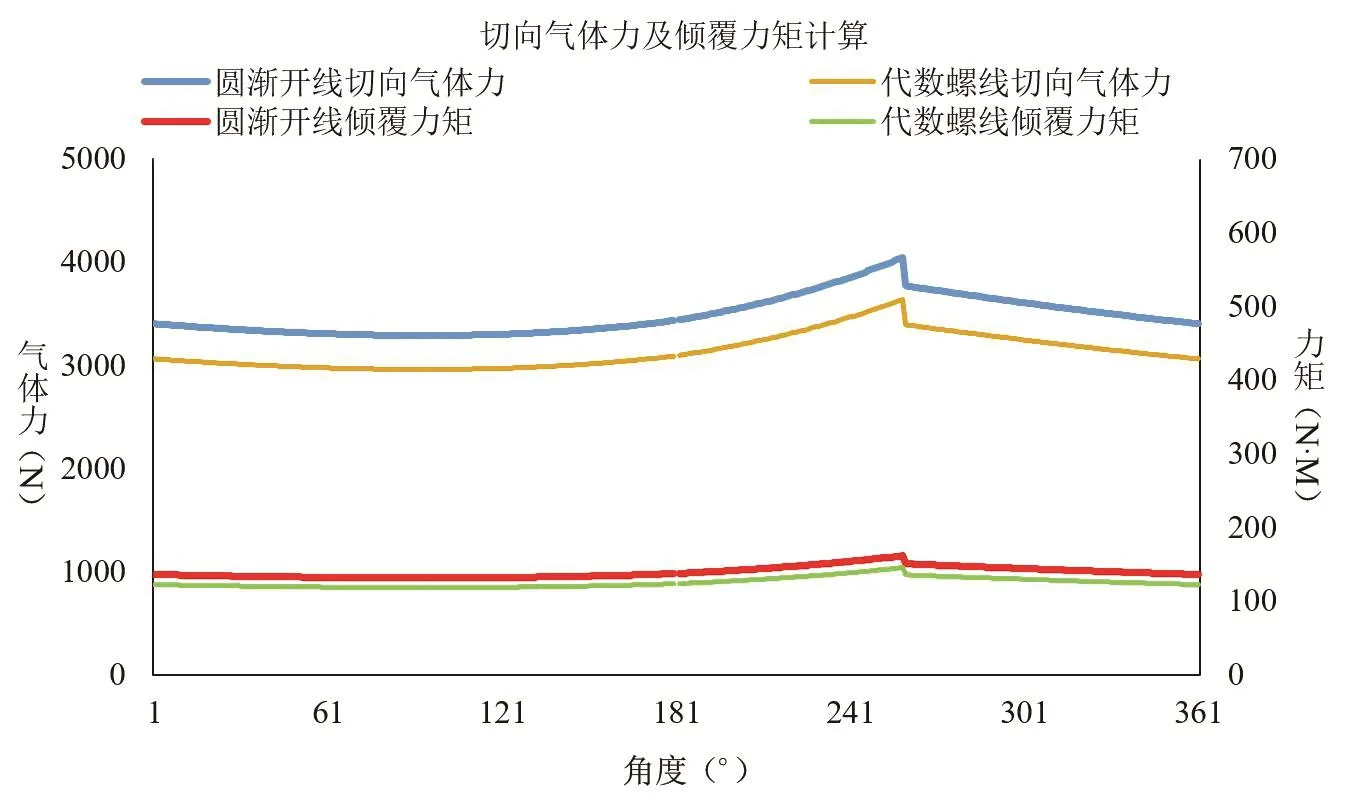
图9 代数螺线与圆渐开线切向气体力及力矩对比

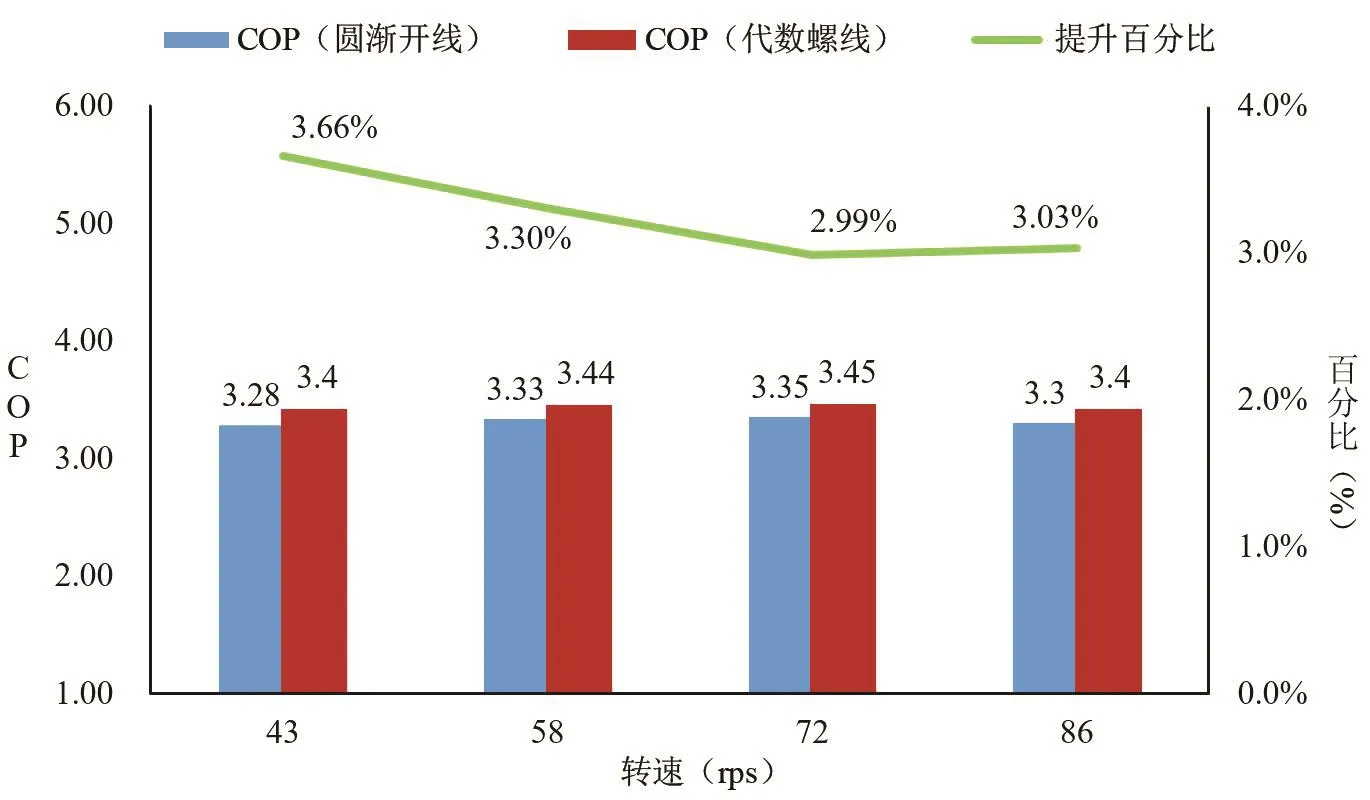
图10 代数螺线与圆渐开线COP对比

3.4 性能测试对比

上述理论分析了代数螺线同比圆渐开线型线的优势。图10为ARI工况下不同频率的实测性能对比。通过图10测试数据可知，在标况ARI工况不同频率的情况下，代数螺线型线相对圆渐开线型线在性能上有3%左右的提升，频率越低提升效果越好，说明代数螺线泄漏线长度的减少会带来低频泄漏量的减少。综合数据可以明显看出，代数螺线在性能提升方面有一定的效果。

4 结论

综上所述，代数螺线型线同比圆渐开线型线相比具有一些明显优势：

（1）代数螺线是一种可变壁厚的结构，可将涡旋壁厚设计成由吸气端到排气端逐渐增大的结构，通过壁厚改变提高涡卷强度，从而提升可靠性。

（2）在吸气容积一定的条件下，同比圆渐开线型线，代数螺线涡旋尺寸可以更小型化，泄漏线长度更小，可减少涡旋气体力及倾覆力矩，可提升性能。也说明在涡旋外径及齿高相同的条件下，代数型线可以有更大的吸气量和更高的压比设计。