海洋物性监测小型浮标稳性设计
2020-08-05梁冠辉薛宇欢孙宝楠陶常飞官晟周兴华
梁冠辉薛宇欢孙宝楠陶常飞官 晟周兴华
(自然资源部 第一海洋研究所,山东 青岛266061)
科技部重大科学仪器专项“海洋物性参数监测仪”旨在摆脱我国海洋传感器核心部件依赖进口、关键技术被“卡脖子”的现状[1-5],响应国家“建设海洋强国,关键技术要我们自己来研发”的要求,研制具有自主知识产权、质量稳定可靠、核心部件国产化的海洋气象传感器、海洋物性参数监测仪数据采集系统和数据服务平台等,并且以海洋气象水文浮标[3-7]为载体于2 000 m以深海域开展一年以上的应用示范,实现温度、压力、湿度、风场、雨量和太阳辐射等海洋气象水文多参量的高精度测量。
深远海海况复杂多变,浮标长期运行过程中会出现横摇幅度过大的情况,甚至倾覆[6-10],而且浮标运输、布放和维护成本相对近海都高出很多,因此,设计稳定性良好的浮标是开展长期连续海洋应用示范和获取高质量气象水文数据的关键。浮标稳性研究的主要方法有:理论计算、数值模拟和港池试验等,本文中的浮标尚处在设计阶段,故采用理论计算的方法设计其稳性,以达到优化浮标设计方案的目的。很多学者也采用理论计算方法开展海洋中的船舶、平台和浮标的稳性研究,如Venkatesan等[11]使用理论计算方法得到用于印度洋海啸监测的圆柱浮标的稳性,并且使用等比例缩小的浮标模型在水池中进行了试验,验证了该柱状浮标设计合理,稳性理论计算准确;汪洋等[12]计算了半潜船装载特定货物前初稳性高的最高限值,得到了初稳性高度可行域,并由此提出提高船舶航行稳性的方法;邓露等[13]研究半潜型浮式风力机平台的初稳性高度限值和完整稳性的影响因素,并将计算结果作为半潜型浮式风力机平台的设计参考。本文以流体静力学为基础,参照船舶静力学原理[14]及波浪理论[15],计算浮标的初稳性和大倾角稳性[16-17],将计算所得的稳性参数作为浮标设计过程中调整其重心、浮心和吃水等参数的依据,并初步判断浮标设计方案的优劣。
1 环境参数与浮标设计参数
1.1 浮标极限生存环境
浮标的极限生存环境是指该浮标在工作时所能承受的海洋气象水文环境极值[18]。准确地评估浮标极限生存环境参数是设计长期稳定可靠的浮标平台的先决条件。目前,海洋浮标出现问题超过半数,主要是因为设计前对浮标极限生存环境条件估计不足,导致浮标性能无法满足实际海况的工作要求。本文参考海洋行业标准《小型海洋资料浮标》[19]和《海洋资料浮标原理与工程》[20]中对于浮标极限生存环境参数的要求,结合浮标工作海域的实际海况,提出海洋物性监测仪浮标的极限生存环境参数,如表1所示。

表1 浮标极限生存环境参数Table1 Extreme living environmental parameters of the buoy
1.2 浮标设计参数
综合分析需搭载的所有国产气象水文传感器对浮标连续供电能力和安装空间的需求,考虑到深远海浮标长途运输和布放时所用科考船的条件,设计浮标如图1所示。浮标采用直径为3 m的圆盘式结构,主要由上架、浮体、舱体和下架组成。其中,上架主要搭载各种传感器及太阳能电池板,材质为铸铝,这样既能保证浮标上架的强度,又具有密度低的优点,有利于降低浮标整体重心,提高浮标的稳性;浮体采用PE材料,表面喷涂聚脲,以保证浮体具有足够的强度和防腐性能;舱体包括仪器舱和电池舱,由316不锈钢制成;下架支撑整个浮体,安装有配重、牺牲阳极和锚系连接装置等,材质与舱体相同。浮标主要参数见表2。
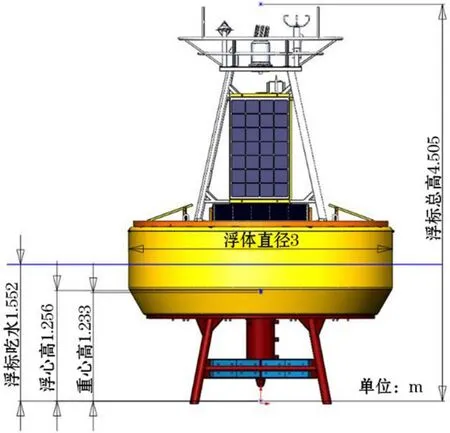
图1 小型浮标设计Fig.1 Design of the small buoy

表2 浮标主要参数Table 2 Main parameters of the buoy
2 浮标稳性计算
浮标在水平外力作用下偏离平衡位置会发生倾斜,当外力消失后,能自行恢复到最初平衡状态的能力称作浮标的稳性。包括初稳性和大倾角稳定:初稳性指浮标倾斜角度小于10°的稳性;大倾角稳性是指倾角大于10°的稳性[21]。
2.1 初稳性
浮标在水平方向上倾斜φ角度后,浮心B沿某一曲线移动至新的浮心B1,新的倾斜水线为WφLφ,M点为浮标的初稳心,为浮标的稳心半径r,即稳心与浮心的垂向距离[22-23](图2)。当倾斜角度φ≤10°时,曲线近似为圆弧,M点近似为曲线的圆心为曲线的半径,因此在小倾角条件下,稳心半径r的计算公式为
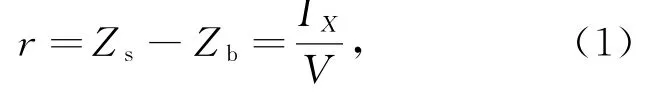
式中,Zs稳心垂向坐标;Zb为浮心垂向坐标;IX为浮体水线处横截面积对其形心X轴的面
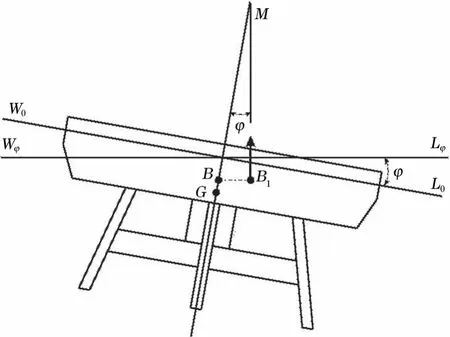
图2 浮标初稳性示意图Fig.2 Schematic diagram of the initial stability of the buoy
浮标要具有稳定的平衡状态,除了稳心需高于重心,还需有合理的稳心高度,在初稳性计算中初稳心高度是衡量浮标初稳性好坏的重要指标[24-25],初稳心高度(Hs) 计算公式为

式中,Zg为重心垂向坐标。Zb与Zg可利用浮标设计图(图1)统计得到,将文中浮标参数代入式(1)和式(2)计算,可得浮标的稳心半径,值为1.033 m,进而求得初稳心高度为1.056 m。《国内航行海船法定检验技术规则(2011)》[26]中海洋浮式结构初稳性对初稳心高度的要求是不小于0.15 m,文中设计浮标的初稳心高度远大于规范要求值,说明该浮标设计满足此项初稳性要求。
浮标的初稳心高度还决定了浮标在小倾角自由摇摆时的运动特性。浮标横摇固有周期与初稳心高度有直接关系,且其随着初稳心高度的增加而减小,即初稳心高度越大,浮标的横摇周期越短。若初稳心高度过大,在海洋中遇到风浪时,浮标会产生急剧的摇摆,以致降低浮标的安全性和数据采集的精准性。因此需通过计算浮标的横摇固有周期来判断浮标初稳心高度设计的合理性,浮标横摇固有周期Tφ计算公式为

式中,J为浮标相对于X轴的转动惯量;ΔJ为浮标体附连水质量相对于X轴的转动惯量,一般认为ΔJ≈0.2J;ρ为海水密度。

利用式(3),可进一步求得浮标在横摇角与波浪斜率较小的情况下的最大横摇角φmax,其计算公式为式中,H为浮标所在海域波浪的最大波高;L为浮标所在海域波浪的波长;T为浮标所在海域波浪周期。由式(4)可以看出,当浮标的固有周期Tφ与所在海域的波浪周期T相近时,式中分母T2-T2φ趋近于0,此时浮标最大横摇角将陡然增大,浮标将会与波浪发生谐振,导致浮标的安全性降低。
将文中设计浮标的直径、质量和转动惯量等参数分别代入式(3)和式(4),可求得浮标横摇的固有周期为5.2 s,在波浪中的自由最大横摇角为15.3°,浮标布放海域的波浪周期为12 s。可见,设计浮标的固有周期避开了布放海域的波浪周期,工作时浮标与波浪不会发生谐振,该浮标具备足够的安全性。
2.2 大倾角稳性
大倾角稳性用来判断到浮标在布放海区所能承受的极限海浪,或者计算浮标丧失稳性而倾覆时的极限横倾角度。大倾角稳性主要是计算浮标在静力作用下的静稳性和动力作用下的动稳性,以浮标的稳性力臂来反映浮标的稳性。故欲求得浮标的大倾角稳性,需先求得浮标的静稳性力臂曲线和动稳性力臂曲线[27]。
2.2.1 静稳性曲线
本文采用变排水量法计算浮标的静稳性力臂,首先得到浮标静稳性力臂随浮标横倾角的变化曲线,再对静稳性力臂曲线进行积分得到浮标动稳性力臂曲线。在计算过程中,因为浮标上架形状不规则且入水体积远小于浮标体与下架,所以为了提高计算效率,本文忽略了浮标上架的出水与入水体积,仅考虑浮标体与下架的出水与入水体积。
横倾后,浮标受力如图3所示,浮标排水体积计算公式:
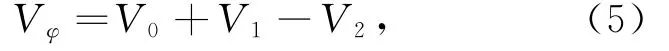
式中,Vφ为浮标横倾时的排水体积;V0为浮标正浮时的排水体积;V1为横倾时浮标入水楔形体积;V2为横倾时浮标出水楔形体积。
根据合力矩原理,结合图3得Vφ对于NN′的体积静矩Mφ:

式中:l1为浮标入水楔形V1浮力作用线与倾斜水线WφLφ的交点A到旋转点O的距离;l2为浮标出水楔形V2重力作用线与倾斜水线WφLφ的交点B到旋转点O的距离;l0为浮标平衡状态时排水体积V0浮力作用线与倾斜水线WφLφ的交点F到旋转点O的距离,计算公式为l0=(d0-dKB0)sinφ+c·cosφ,其中dKB0为浮标底面中心点与正浮浮心的距离。由于浮标倾斜时入水和出水楔形不规则,不同倾角的V1,l1,V2和l2通过三维制图软件统计所得。
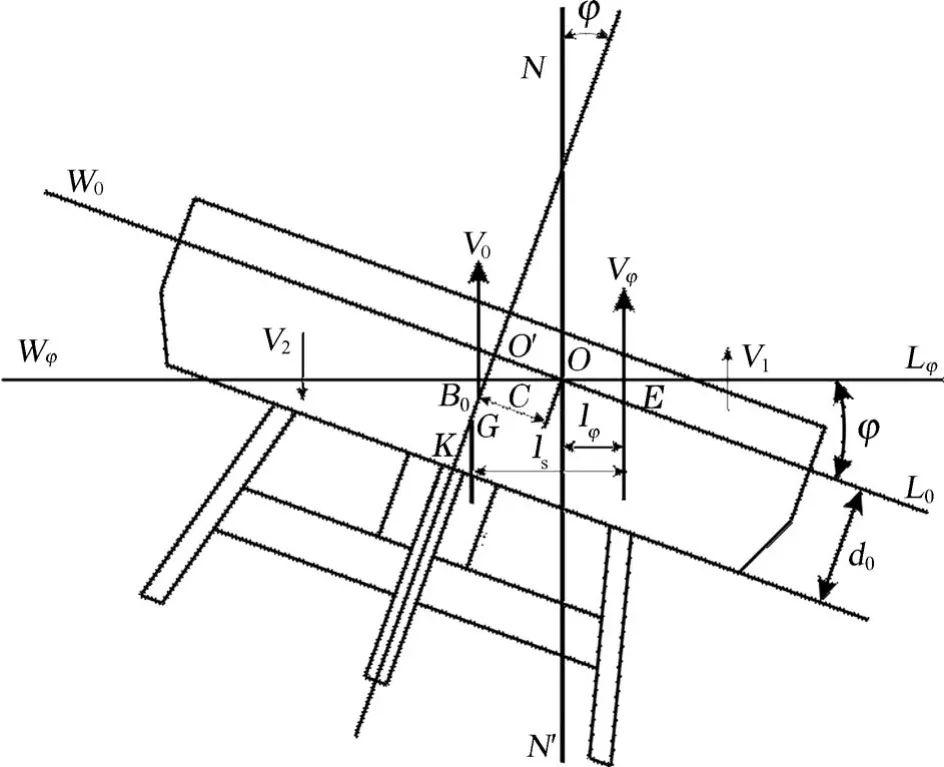
图3 浮标静稳性示意图Fig.3 Schematic diagram of the static stability of the buoy
由式(5)和式(6)可得,浮标浮于倾斜水线WφLφ时,浮力作用线至轴线NN′的距离为
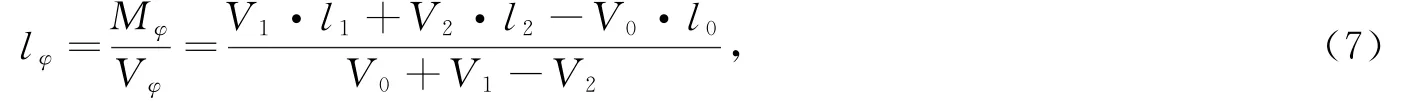
则浮标的静稳性力臂ls的计算公式为
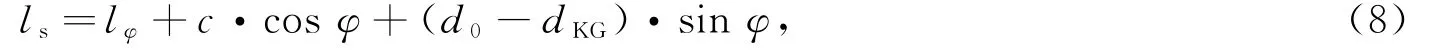
式中,d0为浮标平衡状态时的吃水深度;dKG为浮标平衡状态时重心G到浮标横截面底部中心K的距离;c为偏离值,指的是浮标倾斜后的旋转点距离平衡状态水线中心的距离。旋转点取在入水一侧,c视浮标吃水线至浮体上沿的距离与吃水比而定,比值越小,偏移越大,以便在大倾角水线下入水楔形与出水楔形的大小大致相同。根据设计的浮标的吃水、型宽等参数以及参考其他人的工作经验,本文中取c值为0.1 m。
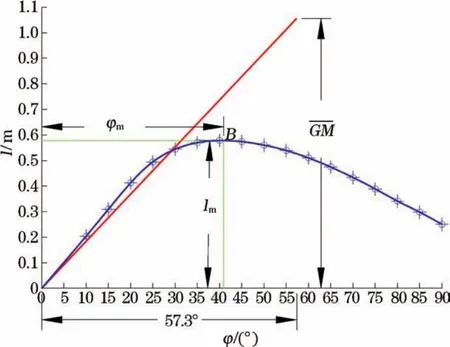
图4 浮标静稳性曲线Fig.4 Static stability curve of the buoy
一般情况下,海洋浮体结构的大倾角稳性计算中横倾角最大取值范围为70°~80°[28],文中计算时浮标的横倾角取值范围为10°~90°,取值间隔为5°。通过文中所述计算流程,计算得到静稳性力臂曲线(图4)。
由最大复原力臂lm可以求得浮标所能承受的最大静态横倾力矩,若外来的恒定横倾力矩超过浮标所能承受的最大静态横倾力矩,浮标将倾覆。静稳性曲线最高点B对应的横倾角为极限静倾角φm,在浮标横倾角达到极限静倾角之前,浮标处于稳定平衡状态;当浮标横倾角超过极限静倾角后,浮标处于不稳定平衡状态。静稳性曲线下降段复原力臂等于0 m时对应的浮标横倾角称为浮标稳性消失角。图4中,该浮标的极限静倾角约为41°,最大复原力臂约为0.58 m,稳性消失角超过90°。《国内航行海船法定检验技术规则(2011)》[26]中对于海洋浮体结构的大倾角稳性的要求为横倾角等于30°处的复原力臂应不小于0.2 m,最大复原力臂对应的横倾角应不小于25°,稳性消失角应不小于55°。将本文中的结果与标准要求比较分析,结果表明:本文设计的浮标完全满足技术规则的要求,具备足够的静稳性。
3.2.2 动稳性曲线
静稳性曲线的计算是假定浮标受到外力矩的缓慢作用产生横倾,并且倾斜过程中浮标的角速度一般认为近似等于零。但是,浮标在海洋中实际运行时,经常会受到阵风的突然吹袭和海浪的猛烈冲击等情况产生的外力矩作用。这种外力矩的突然作用会使浮标产生极快速的倾斜,这时浮标的角速度较大,不能忽略为零。在这种运动过程中,当复原力矩等于外力矩时,外力矩虽然已经不能使浮标继续倾斜,但是由于浮标具有一定的角速度,在惯性的作用下会继续倾斜。只有复原力矩做的功抵消外力矩做的功时,浮标的角速度才能变为零而停止倾斜,因此,该运动状态需进行动稳性计算来判断其稳性[29]。
浮标的动稳性以复原力矩所做的功来表示[30]。当浮标横倾至φd时,复原力矩MR的变化规律由静稳性曲线表示,其做功计算公式为
式中,V为浮标排水量;ld为浮标动稳性力臂;ls为静稳性力臂。由式(9)可得出动稳性力臂ld计算公式为因此,动稳性曲线是静稳性曲线的积分曲线,本文中计算所得动稳性曲线如图5中红线所示。与静稳性曲线分析过程相同,动稳性曲线分析过程中也需求得最大动稳性横摇角φ0,其计算公式为

式中,C1,C2,C3和C4为系数,根据浮标的体积和质量参数查表[26]所得:C1=1.21,C2=0.68,C3=0.02,C4=0.885,可求得最大动稳性横摇角φ0=23.2°。
以纵轴为对称轴将动稳性曲线沿横坐标轴向负方向延长,如图5中蓝线所示。A点为动稳定曲线延长线终点,其横坐标绝对值为最大动稳性横摇角φ0。B点纵坐标与A点相同,横轴与A点相距1 rad(57.3°)。C点为动稳性曲线过A点的切线与横轴过B点的垂线的交点。线段BC长度即为最小倾覆力臂lq,本文中浮标的最小倾覆力臂为0.277 6 m。
动稳性曲线的重要应用是计算浮标的稳性衡准数K[26],其计算公式为

式中,lq为最小倾覆力臂;lf为风压倾斜力臂,计算公式为其中,p为计算风压,根据浮标布放海域和风力作用力臂查表[26]所得;Af为浮标受风面积,即浮标吃水线以上部分的侧投影面积,Z为浮标受风面积中至吃水线的距离,即风力作用力臂,V为浮标排水量,Af,Z和V可通过浮标设计图统计所得。
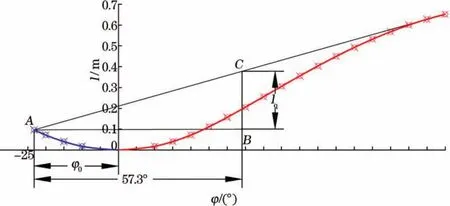
图5 浮标动稳性曲线Fig.5 Dynamic stability curve of the buoy
经过计算,文中浮标的风压倾斜力臂为0.220 9 m。将已得的lq和lf代入式(11)求得本文浮标的稳性衡准数K=1.26,满足《国内航行海船法定检验技术规则》[26]中浮体稳性衡准数≥1的要求,该结果表明,本文设计的浮标具备足够的动稳性。
4 结 论
以浮标工作的深远海环境参数和浮标的浮性参数为基础,开展了浮标初稳性和大倾角稳性计算,计算结果为:浮标的初稳心高度为1.056 m,稳心半径为1.033 m,自由横摇固有周期为5.2 s,自由最大横摇角为15.3°,最大复原力臂为0.58 m,极限横倾角为41°,稳性消失角>90°,最小倾覆力臂为0.27 m,稳性衡准数为1.26,结果均优于《国内航行海船法定检验技术规则》对稳性的要求。这些结果表明:本文设计的浮标具备足够的复原力矩,有足够的抵抗倾斜力矩的能力,避开了布放海区的主要波浪周期,保证浮标遇到风浪不会剧烈地摇摆,在大风、大浪的极限海况下,浮标受风浪作用倾斜后具备足够的复原力矩,以防止其倾覆。
影响浮标稳性的几个重要参数有:浮标重心、浮标型宽、浮标排水、浮标受风面积和风力作用点等。在合理的范围内降低重心和增加排水有利于浮标初稳心高度、复原力臂和稳性消失角的提高。浮标型宽影响浮标的水线面积惯性矩、复原力臂和极限静倾角,增大浮标型宽可以提高其水线面积惯性矩和复原力臂,增加浮标初稳性,但是会降低其极限静倾角,降低浮标的静稳性。因此,设计浮标时应在设计要求的范围内,合理设置与组合浮标相关参数以达到最优的方案,确保浮标具备足够的初稳性、静稳性和动稳性。在后续的工作中需要使用研制的浮标在港池或者近海开展验证试验,通过实测浮标横摇和纵荡数据来验证浮标稳性理论计算是否正确。
