基于灰度预测的变长度经验模态分解方法研究
2020-08-05张晓波刘保华于凯本刘苗杨志国于盛齐宗
张晓波刘保华于凯本刘 苗杨志国于盛齐宗 乐
(1.自然资源部 国家深海基地管理中心,山东 青岛266237;2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室,山东 青岛266061;3.中国海洋大学 环境科学与工程学院,山东 青岛266100;4.青岛海洋科学与技术试点国家实验室 公共关系部,山东 青岛266061)
对于一般的非线性非平稳信号,信号特征多表现为时变和频带混叠,导致有效信号往往存在于某一个或几个频带中,因此从原始信号中分离和提取有效信号是信号处理的重要研究内容之一。经验模态分解(Empirical Mode Decomposition,EMD)是由美籍华人Huang等[1]于1998年提出的一种信号谱分解方法。该方法的核心思想是任何复杂的信号都可以被分解成有限个固有模态函数(Intrinsic Mode Function,IMF)和1个剩余分量之和。因为该方法是在基于信号本身特征的基础实现的分解,它与基于傅里叶变换的方法相比,具有更强的自适应性和局部时频分析能力,因此在分析非线性和非平稳信号中具有很高的实用价值。
虽然经验模态分解被认为适合分解非线性和非平稳信号,但由于其提出时间较短,缺乏理论支撑,需要解决的问题很多,例如在应用经验模态分解时信号边界很容易产生信号分解失真问题,即端点效应。其产生原因是在基于EMD方法进行信号分解时,由于端点处为非极值点,在计算信号包络时会出现端点处不能完全包络以及由三次样条插值引起的过冲和欠冲等问题,这会使得分解后的IMF函数误差过大,从而对信号分解结果的准确度产生严重的影响。
目前国内外学者已提出了多种压制端点效应的方法,如特征波法[1],波形匹配法[2],镜像圆周对称延拓法[3-4],极值点镜像延拓法[5],基于时间序列预测模型(Auto Regression Moving Average,ARMA)的延拓方法[6],基于神经网络的时间序列预测方法[7-8]以及基于灰度预测模型的延拓方法[9]等。但这些方法在应用中均存在一定程度的不足。例如,特征波法的问题在于非平稳非线性信号的两端具有的波形特征不一定相同,所以选择合适的特征波比较困难;波形匹配法在实际应用中计算效率相对低下;镜像圆周对称延拓法则将端点直接做为极值点进行处理,反复迭代计算过程中会引起端点值的失真;极值点镜像延拓法通常把距离端点最近的极值点作为镜面点对信号进行延拓,当端点不是极值点时还需对信号进行截断处理,如果数据较短,则端点效应的压制会失效;基于时间序列预测模型的延拓方法和基于神经网络的延拓方法两种方法预测效果较好,但存在计算效率低下和对大数据量和信号周期化的依赖等问题;基于灰度预测模型的延拓方法根据已知的极值点位置和数据利用灰度预测模型预测未知的极值点位置和数据,与前述其他方法相比,该方法在计算效率和抑制效果等方面均有显著改善,但由于灰度预测方法本身的限制,其效果仍有待提升。
本文围绕经验模态分解中的端点效应问题,对常规基于灰度预测模型的端点延拓方法[9]加以改进,实现了基于灰度模型的变长度经验模态分解方法,并利用仿真数据进行结果对比。
1 EMD基本原理及端点效应
1.1 EMD基本原理
EMD算法基于任何信号都是由有限个固有模态函数组成,每一个固有模态函数都可以通过以下方法得到:
假设原始信号为x(t),找出信号的全部极值点,将所有局部极大值点和所有局部极小值点分别进行拟合得到envmax(t)和envmin(t),这样使所有的信号数据包含在2条包络线之间。2条包络线的平均值记为m1(t),其表达式为

将原信号x(t)减去m1(t)得到一个新信号h1(t),即h1(t)=x(t)-m1(t),此过程称为筛分。若h1(t)满足IMF条件[5],则h1(t)为第1个固有模态函数;若h1(t)不满足IMF条件,则将所得的h1(t)序列作为待处理数据,重复进行上述的筛分工作,直到所得序列满足IMF条件为止。这样便得到信号x(t)的第1个固有模态函数,记为c1。将c1从x(t)中分离出来,可以得到去除掉高频成分后的剩余部分r1=x(t)-c1,然后把r1作为原始数据重复以上过程,可以得到x(t)的第2个固有模态函数c2。以此类推,如果最终得到剩余分量(rn)比预定的误差要小,或当rn变成1个单调函数不能再继续筛分时,则停止上述分解过程。最终原始信号可以表示为

式中,ci为IMF分量。
1.2 端点效应
在EMD分解过程中,对极小值和极大值包络的求取通常采用插值的方法。当信号端点处不为极值点时,包络计算将产生明显误差,由此分解得到的第i个IMF分量比第i-1个IMF分量在端点处会由于误差累计产生更大的误差。与此同时,误差还会由数据两端向内传播,从而导致整个分解过程失去意义。

这里对信号端点作举例说明。设原始信号为式中,t∈[0,0.3],采样频率为10 000 Hz,对该信号进行经验模态分解时需要求取其极大值包络、极小值包络以及包络的均值(图1)。
由图1可见,如果端点处不是极值点,那么求取的包络在端点处就会出现“欠冲”或“过冲”现象,从而导致计算过程中在端点处出现误差。
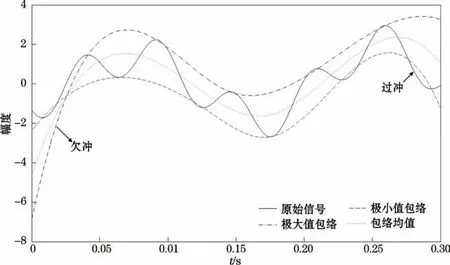
图1 经验模态分解的端点效应Fig.1 Edge effect of empirical mode decomposition
2 基于灰度模型的经验模态分解方法
根据前文所述,为了压制EMD的端点效应,需对端点处的极值点进行有效预测[6]。因此这里利用一阶单变量灰度预测模型算法对端点处极值点实现预测,并基于广泛使用的三次样条插值方法进行包络计算。
2.1 一阶单变量灰度预测模型
定义X(0)为预测模型的数据集合
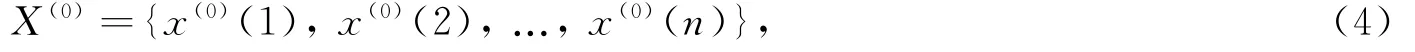
X(1)为X(0)的一次累加生成数序列
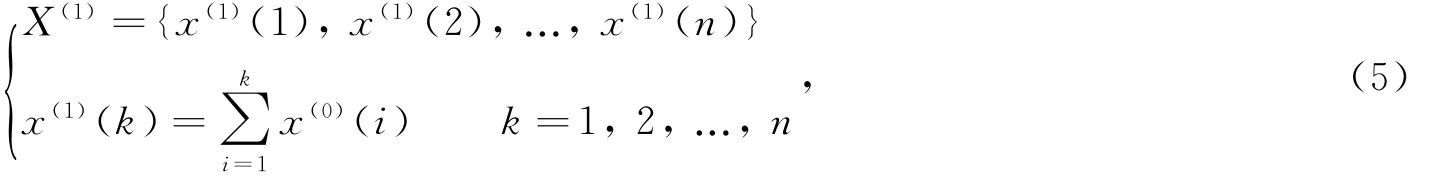
Z(1)为X(1)的紧邻均值生成序列

假定建模序列同号,则其累加生成数序列为单调序列。如果将这个单调序列用指数曲线进行拟合,则该序列可以写成的微分方程为

该式的解为

式中,a,b是待定系数。其中a,b是待定系数。

式(7)通常被称为上式的白化方程或影子方程。设为未知向量则的最小二乘估计满足

根据以上论述,式(9)所示的灰色微分方程的时间响应序列为
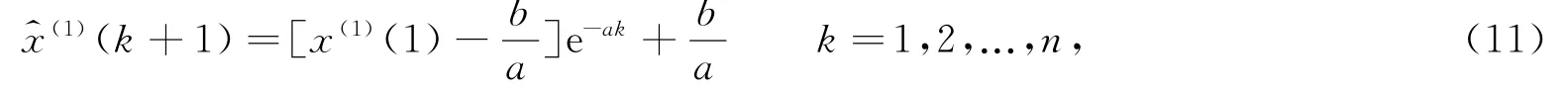
还原值为
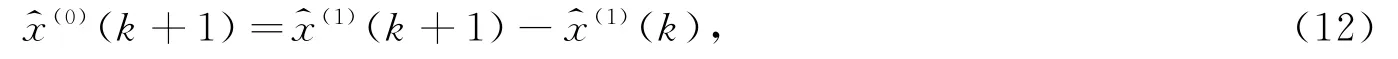
此即预测方程。
2.2 残差模型
对于上文中得到的预测模型,其精确程度可通过残差值进行检验。根据x(0)(i)与建立绝对残差序列
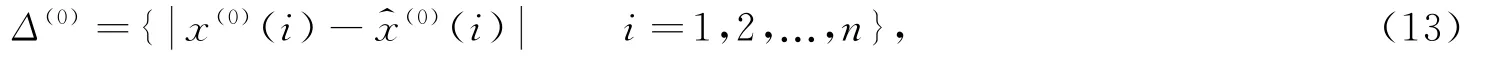
及相对残差序列
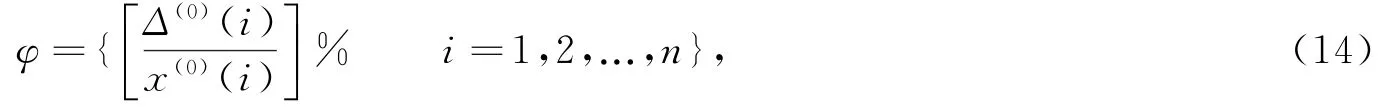
进而得到平均相对残差

给定α,当,且φn<α成立时,称所求出的预测模型为残差合格模型。
此外,利用残差值还可对预测模型值进行修正,令残差值序列为
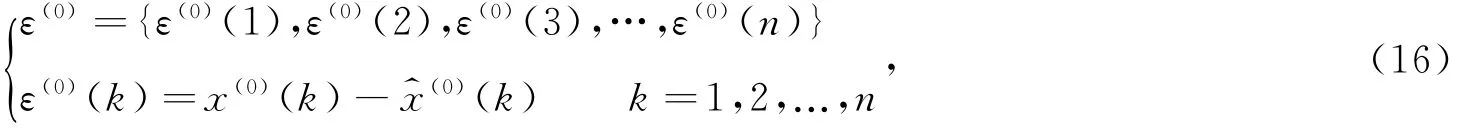

式中,δε为校正权重系数,为残差模型的未知向量利用可得修正后的预测模型值。
则修正模型写作
2.3 灰度预测流程
对于符号相同的数据,利用灰度预测方法往往能够得到较好的预测结果,因此,为使原始数据满足这个条件,可对原始数据x(0)(t)(t=1,2,3,…,n)做如下变换:

式中,xmax和xmin是x(0)(t)的最大值和最小值。对进行灰度预测得到预测数据然后利用反变换式
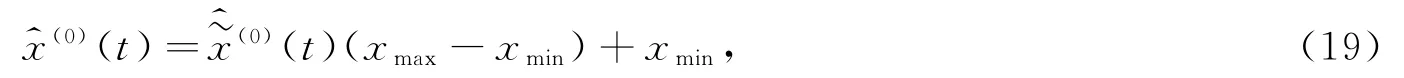
得到原始数据x(0)(t)的预测值。
灰度预测模型的算法流程如下:预测的次数为m,预测的序列为
3)根据式(10)构建矩阵B和Y,并计算,求得[a1,b1]T;
4)对于t=1,2,3,…,n,将[a1,b1]T代入式(11)求得
6)计算原始序列x(0)(t)与的相对残差序列φ,并计算平均相对残差。给定α,当,且φn<α成立时,称模型为残差合格模型;当φ>α或φn>α时,计算残差模型输入数据ε(0)(t),并计算残差模型和修正模型,利用修正模型求得,然后重复步骤5)和6),直至得到残差合格模型。
7)对于t=n+1,…,n+m,利用修正模型求得进而求得最后可得到原始数据x(0)(t)的全部预测值。
2.4 基于灰度预测的端点延拓
基于灰度预测的端点延拓方法主要用于极值点序列的延拓,利用已知的n个极值点位置和数据,预测m个未知的极值点位置和数据。以极大值的延拓为例,在EMD每次迭代的过程中,当得到极大值点序列之后,分别利用两端的4个已知极大值构建灰度预测模型,然后向两端分别延拓2个极大值点,从而得到新的极大值点序列,极小值点延拓同理可得。
端点延拓的具体步骤如下:假设用于预测的n个极值点的位置序列为lk(k=1,2,…,n),极值序列为vk(k=1,2,…,n);预测出的m个极值点位置序列为lk(k=n+1,n+2,…,n+m),极值序列为vk(k=n+1,n+2,…,n+m)。对于i=1,2,3,…,m,第i个预测的极值点位置li+n可以用{li,li+1,…,li+n-1}进行预测,第i个预测的极值vi+n可以用{vi,vi+1,…,vi+n-1}进行预测。
3 基于灰度预测的经验模态分解的改进
3.1 常规基于灰度预测的经验模态分解方法存在的问题
常规灰度预测模型在端点延拓方面相对于镜像延拓,对称延拓,基于AR模型延拓和基于神经网络延拓方法有更好的效果,但灰度预测方法在应用中仍存在一些问题:
1)存在矩阵B为0的情况:在灰度预测的过程中,需要求解矩阵B,然而由于对数据进行了标准化处理,使得矩阵B中的第1列数据存在全为0的情况,所以导致计算出现问题。
2)极值点位置预测不准确的情况:极值点位置序列存在预测过程中仍大于0的情况,没有对端点处的值做有效预测。例如,存在对极值点位置的预测始终大于0的情况,这样对端点处的包络求取仍存在问题。
3)未考虑端点极值情况导致结果不准确:对复杂多变的信号,特别是在端点处有剧烈变化的信号,若不考虑端点极值情况,预测的结果将导致端点处欠包络。与之相较,极值点镜像延拓法,极值点对称延拓法则能有效解决该问题。
4)信号端点处的污染往往无法避免,并会影响下一阶固有模态函数的精度。
3.2 变长度经验模态分解方法
针对以上问题,本研究提出基于类对称延拓和灰度模型结合的方法进行数据的经验模态分解处理,在EMD分解过程中,对信号做端点延拓实际上都是依靠原有数据的特征做出的预测,对于非线性非稳定信号,如果端点处的变化毫无规律又变化剧烈,通过各种预测方法得到的结果可能都是徒劳。由于预测不可能完全准确,可能多次迭代之后端点处的值出现发散,并将向内污染整个序列。鉴于此,研究通过在端点处向外对称延拓一部分原始信号,使其变成新的信号,在每得到一个IMF分量之后,在两端切掉一定长度的序列,这段序列为预测不准确的序列,切除之后,这种预测不准确序列不会被代入下一个IMF的求解,从而最大程度的保证中间信号不被污染。
基于灰度预测的变长度经验模态分解流程:
1)设原始数据的长度为N,原始数据序列为xi,其中i=0,1,2,…,N-1。设各端延拓的长度为Length,本实验中令Length=N/10,IMF的最大阶数为M,则每次切掉的长度为step=Length/M。
2)建立新的序列,其中i=0,1,2,…,N+2Length-1,对新序列进行赋值;对于k=0,1,2,…,N-1,令x⌒k+Length=xk。
3)根据端点处数据的大小判断延拓的方式,以左端点为例:

式中,当x0的幅值较大时,以该点为对称点做对称延拓;当其幅值介于原始信号最小值ximin与原始信号最大值ximax之间时,以该点为中心点做类中心对称延拓,δ∈[0,1]为权系数。右端点处延拓方式同理可得。
4)然后对新序列进行经验模态分解,其端点延拓方式选择基于灰度模型的延拓。
5)当得到k阶IMF分量之后,将中下标为i=Length,Length+1,…,Length+N-1的N个点的值,赋值给,其中i=0,1,…,N-1。
6)将步骤5)中得到的k阶段IMF分量从步骤4)所述的新序列中减掉,得到剩余分量,其中i=0,1,2,…,N+2Length-1。然后,在剩余分量的两端分别减去step个点的值后得到,且令Length=Length-step,则序列长度为i=0,1,2,…,N+2Length-1,以为新序列再次执行第4),5)和6)步骤,直到满足EMD分解结束的条件。
4 模型仿真实验
模型仿真实验的内容包括基于本研究的方法和灰度预测的EMD方法分别对正弦叠加信号的分解以及非线性非平稳信号分解效果的比较。
4.1 正弦叠加信号的分解
实验中用于分析的信号为
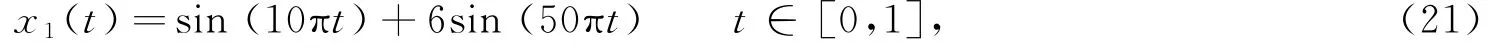
式中,信号的采样频率为500 Hz,合成后的信号如图2所示。在理想条件下,此信号应该被分解成2个正弦IMF分量x11=sin(10πt)和x12=6sin(50πt)以及一个剩余分量x13=0,各分量信号如图3所示。
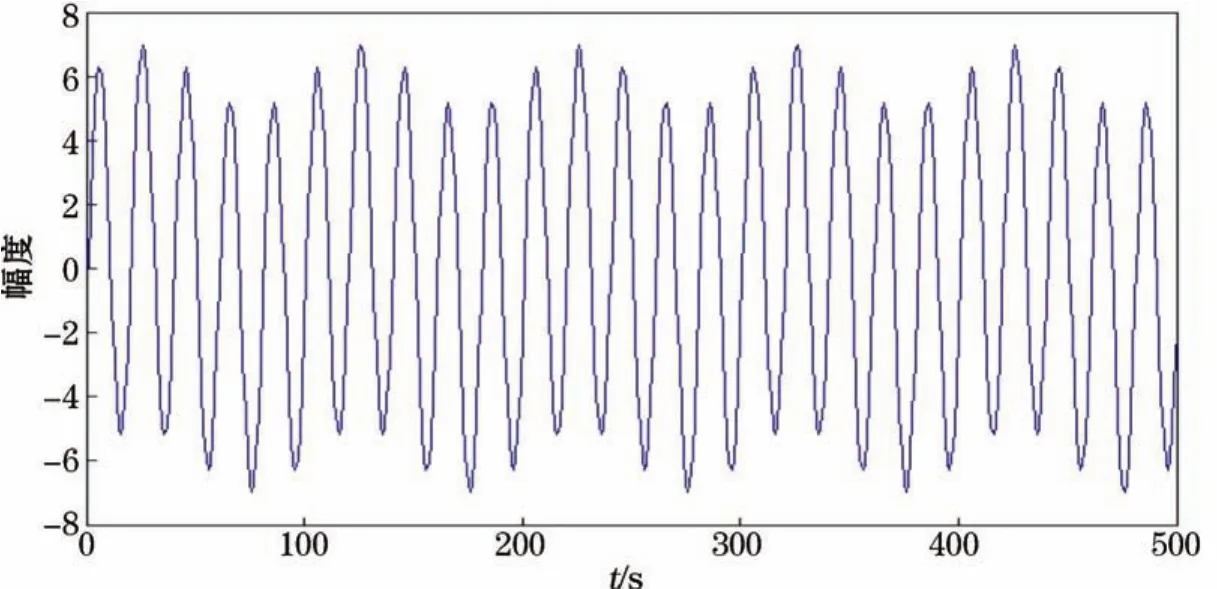
图2 合成信号x 1(t),t∈[0,1]Fig.2 Synthesized signals x 1(t),t∈[0,1]
分别用常规经验模态分解方法、基于灰度模型的方法以及本研究提出的改进方法进行信号分解,可以得到如图4~6所示的结果。利用式(22)对分解得到的IMF分量与理论结果进行误差计算:

式中,IMFi(t)代表在t采样点处第i阶固有模态函数的值。
经计算得到,基于灰度预测的经验模态分解所得结果的误差为(±3.337 8),本研究提出的方法的误差为(±0.025 4)。由此可见,本研究提出的改进方法的效果要优于改进之前的结果。
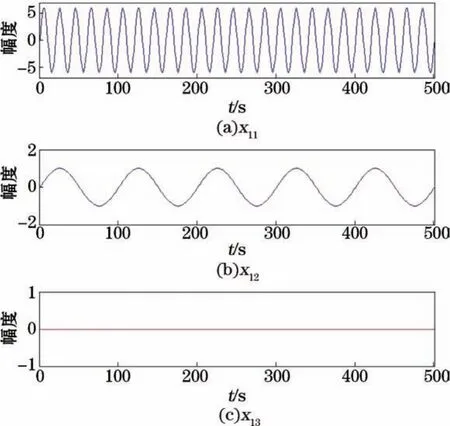
图3 信号子成分x 11,x 12以及x 13Fig.3 Signal subspace x 11,x 12 and x 13

图4 常规经验模态分解的结果Fig.4 Results of conventional empirical mode decomposition
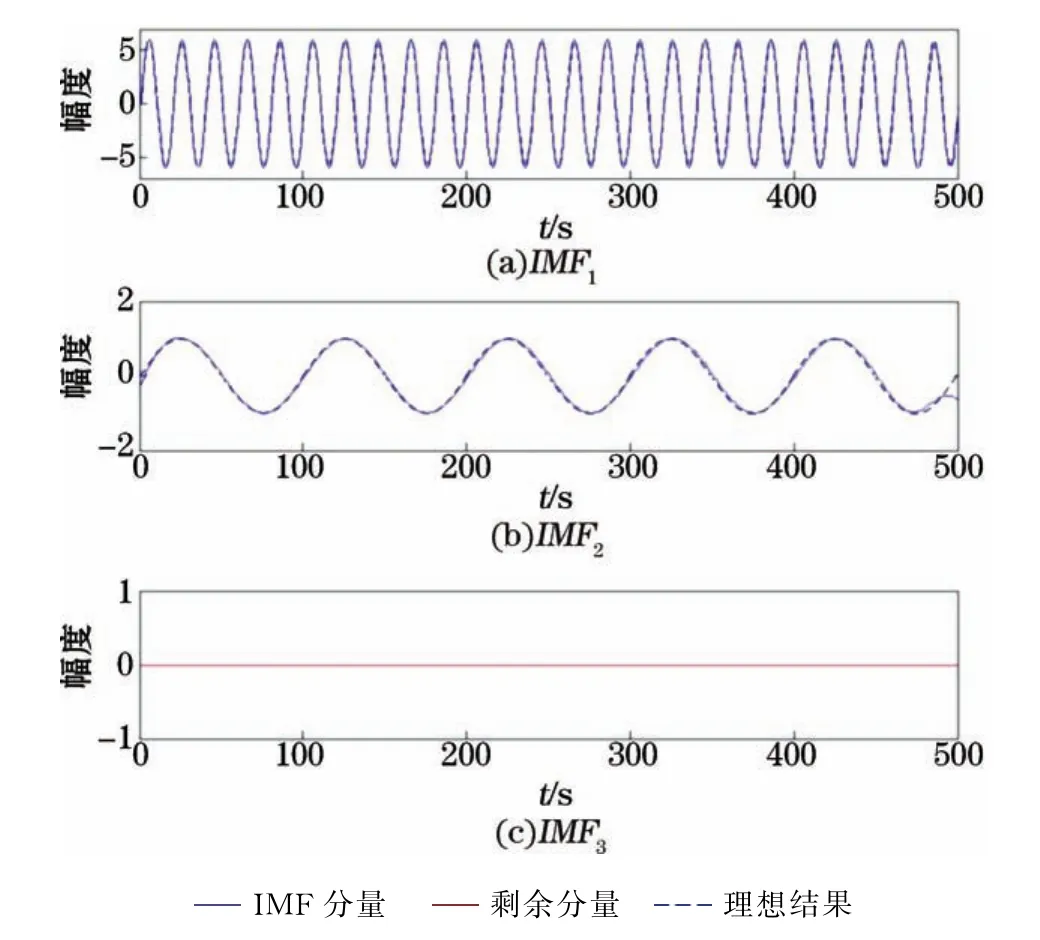
图5 基于灰度模型的经验模态分解的结果Fig.5 Results of empirical mode decomposition based on grayscale model
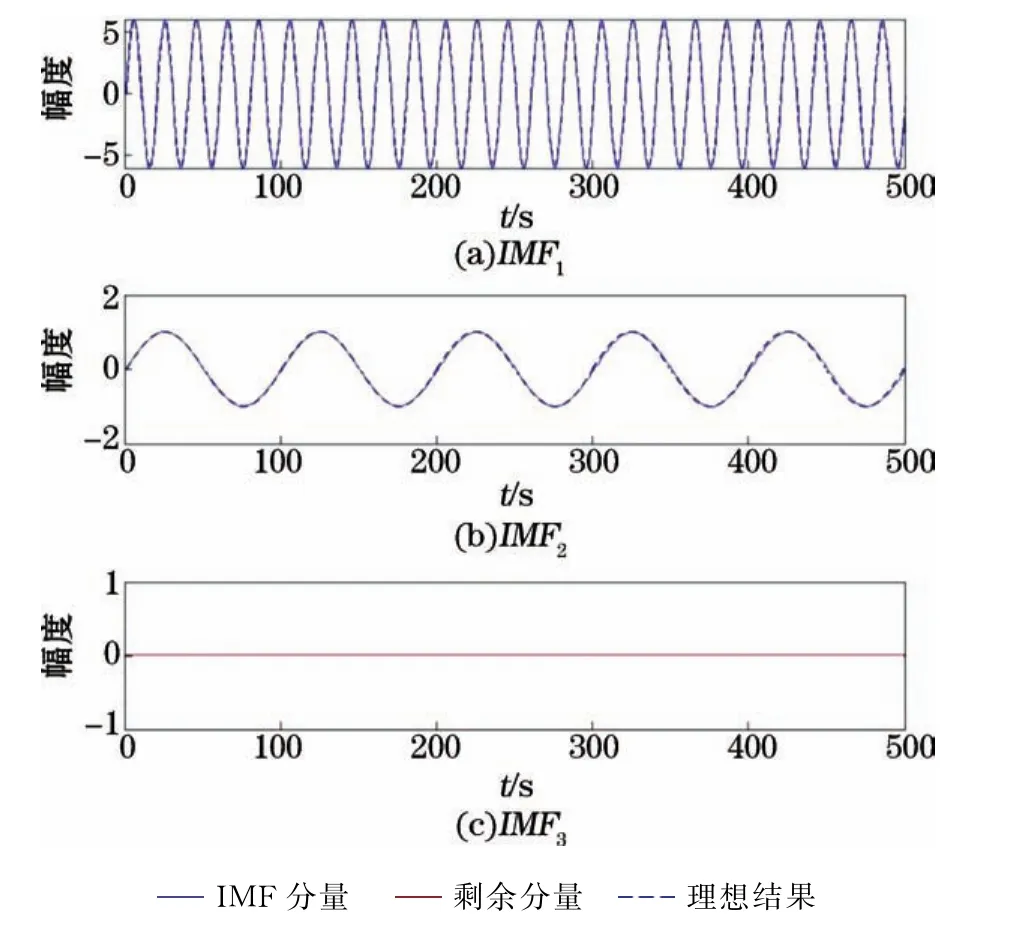
图6 基于本文提出的改进方法分解的结果Fig.6 Results of decomposition based on the improved method proposed in this study
4.2 非线性非平稳信号的分解
本实验中用于分析的信号为

信号的采样频率为1 Hz,其波形如图7所示。在理想条件下,此信号可以被分解成2个正弦IMF分量x21(t)=15sin[(t/80)1.5π]和x22(t)=3sin[(t/100)0.8π]及1个线性剩余分量x23(t)=t/500+5,各分量波形如图8所示。
这里分别用常规经验模态分解方法、基于灰度模型的方法以及本文提出的方法进行信号分解,得到如图9~11所示的结果。对比3种方法的处理结果可以看出:在波形吻合度方面,利用本文提出的方法所得到的固有模态函数与原信号吻合程度最高,而且对信号两端的相位信息处理更准确,基于灰度模型方法所得结果的吻合程度次之,常规经验模态分解方法得到的固有模态函数的个数与原信号不一致,其吻合程度最差;在计算误差方面,利用式(23)分别计算基于灰度模型的方法以及本文所提出方法的结果误差,其中基于灰度预测的经验模态分解所得结果的误差为(±527.8),本研究所提出方法的误差为(±311.619 5),因此本文所提出方法的结果误差更小。综上,本研究提出方法的分解效果要优于未改进之前方法的结果。

图7 原始信号x 2(t),t∈[0,3 000]Fig.7 Original signal x 2(t),t∈[0,3 000]

图8 原始信号的分量x 21(t),x 22(t),x 23(t),t∈[0,3 000]Fig.8 Orignal signal subspace x 21(t),x 22(t),x 23(t),t∈[0,3 000]
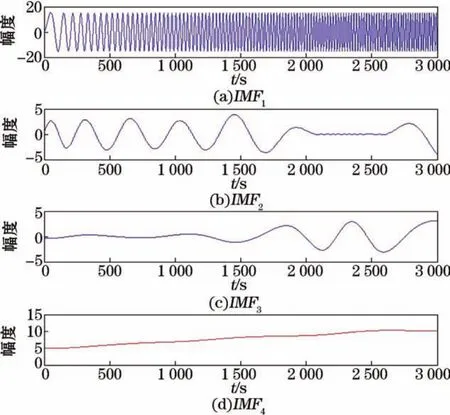
图9 常规经验模态分解的结果Fig.9 Results of conventional empirical mode decomposition
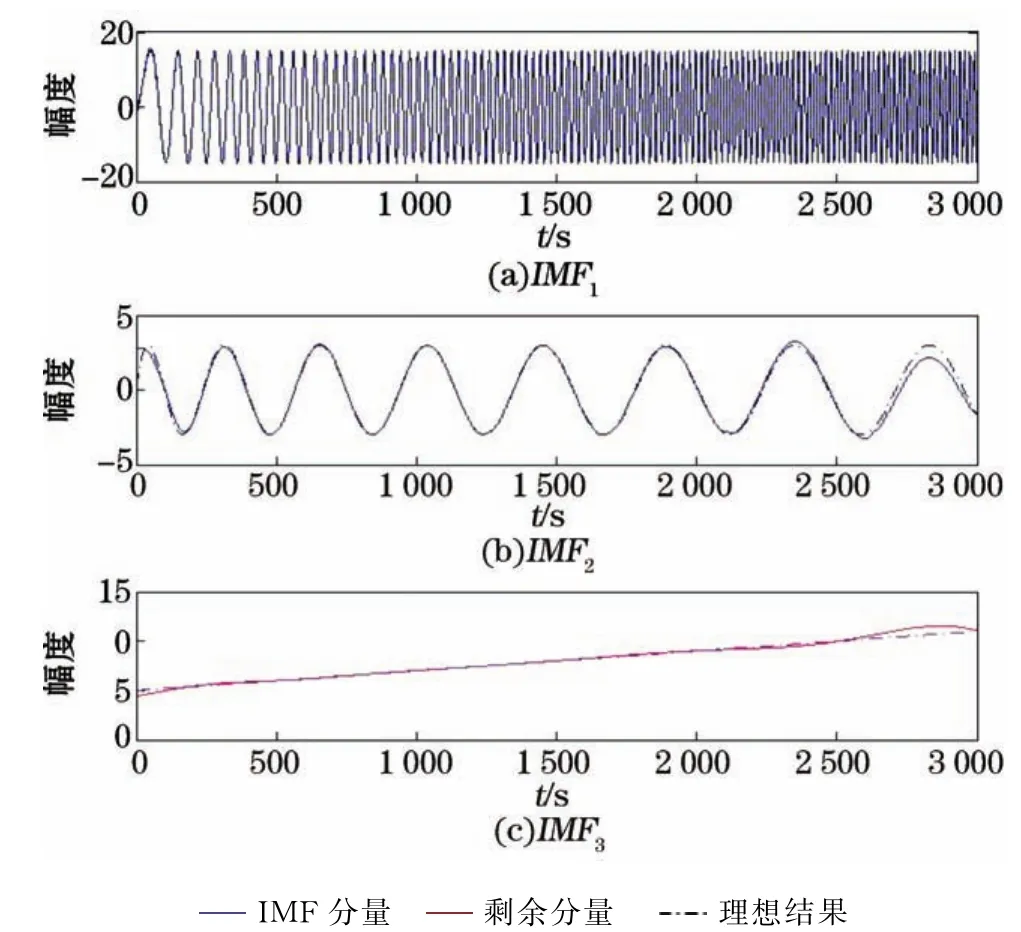
图10 基于灰度模型经验模态分解的结果Fig.10 Results of empirical mode decomposition based on gray model

图11 基于灰度模型的变长度经验模态分解的结果Fig.11 Results of length-varying empirical mode decomposition based on gray model
5 结 论
针对经验模态分解方法中的端点效应问题展开研究,对常规基于灰度预测模型的端点延拓方法存在的问题加以改进,并提出了基于灰度模型的变长度经验模态分解方法,然后利用仿真数据进行对比。模型实验结果表明:
1)对于正弦叠加信号,常规基于灰度预测的经验模态分解所得结果的误差为(±3.337 8),本文提出的方法的误差为(±0.025 4),应用改进方法之后的分解精度得到显著提升;
2)对于非线性非平稳信号,常规经验模态分解方法基于灰度预测的经验模态分解所得结果的误差为(±527.8),用本文提出的方法的误差为(±311.619 5),应用改进方法之后的分解精度仍然得到提升,同时,本文提出的方法对信号端点处相位信息的处理更准确。
