数学课堂如何加强深度学习

广东省开平市金山中学 郑娟馥

在课程开始前，教师需要研究课程目标，明晰设计课程的指导思想和对学生的深层要求。我于2019 年3 月份以《反比例函数复习》一课参加佛山、东莞、江门三市数学学科初三复习教学联合教研活动，由于是复习课，学生对反比例函数知识有了一定的储备，如反比例函数的概念、图像和性质等，然而学生在解决函数图像的综合应用中还存在一定的困难，从而将课程的重点定为反比例函数的图像性质与数形结合思想，教学难点定为反比例函数图像问题的综合运用和深入探究。通过问题的层层递进，深度挖掘反比例函数图像的应用，培养学生数形结合的数学思想，提高学生对知识的综合应用能力。

一、事先评估学生能力

教师上好一节课，不仅要备教材，更重要的是要备学生。在上每一节复习课前，我会充分了解学生对此章节掌握的深度，然后根据学生的情况调整教学方法，筛选习题的难度与数量，让不同层次的学生达到自己应有的水平。以《反比例函数复习》一课为例，由于学生对知识有了一定的储备，所以课前我要求同学们以小组为单位，制作思维导图。通过这个活动，让同学们在课前加深对先前所学知识的复习与巩固，为后面的深度学习打下良好的基础。

二、营造积极的学习氛围

在课堂上，教师应该为学生营造一个安全的舒适的环境，在课堂教学中，我采用小组合作教学的形式，4 人为一小组，小组长轮流。在课堂教学中，我会有意识地设计学生感兴趣、能激发学生讨论的议题，充分发挥学生学习的主动性，培养学生合作互助的素养，深入探讨，培养学生的质疑与批判。在课堂上，我充分相信学生，多一些机会让学生锻炼，如让学生制作思维导图，然后由各小组的学生代表上台进行解说，这样既锻炼了学生表达、知识归纳、分析的能力，更培养了学生的自信心。

三、激活先前的知识

由于学生的水平不同，对知识掌握范围与程度也有所不同，在上课开始时，我经常会挑选一些先前有关知识点的小题让学生进行练习，勾起学生对先前知识的记忆，同时有针对性地设计与新知识有关联的习题，自然地引入新课的学习。在《反比例函数复习》的教学中，基于学生对反比例函数的图像和性质以及k的几何意义有了一定的理解，我通过一道例题勾起学生对旧知识的回忆。

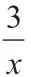
通过练习，学生进一步理解S△OAB=|k|。通过这道习题，让学生加深图中阴影矩形的面积与反比例函数常数k的关系，从而为后面的练习打下基础。

随后，通过变式训练，进一步加深学生对k的几何意义理解，从而形成技能。

（1）如图2，AB∥y轴，则S△O1AB=_。

（2）如图3，AB∥x轴，则S△O1AB=_。

（3）如图4，AB∥x轴，则S△O1AB=_。

（4）如图5，AB∥y轴，则S△O1AB=_。

以上由学生对四个变式进行思考、遇到困难再由小组讨论、研究，师生共同归纳方法，通过问题引领，发散学生的思维，促进学生思维深度交锋，培养学生的分类讨论、数形结合思想并逐步走向“深度学习”。

四、知识内化于心

学生通过小组的合作学习，同伴间的相互交流，开拓视野，也进一步拓宽知识结构，同时学生结合自身的知识结构，重构或者完善自身的知识网络，将新知识内化于心。如在复习反比例函数时，学生通过不同变式图形的认识，通过自己思考以及与同学的交流，真正明白阴影部分面积与反比例函数中常数k的联系，并能灵活地进行应用。

五、知识深度加工

新时代我们需要培养具有创新精神的优秀接班人，在课堂教学中，教师要注重培养质疑与批判精神，深入钻研。如在进行反比例函数复习时，通过问题串的形式，不断将问题逐步加深，培养学生深入探讨钻研，进行深度学习，将对知识的一般理解应用上升到灵活熟练应用的程度，从而实现深度学习的目的。

以《反比例函数复习》一课为例，如图6，将矩形OABC沿坐标轴平移，平移后的矩形有两边在坐标轴上，一个顶点分别在第二、第三、第四象限。

这道例题通过问题串的形式层层递进，拓展学生思维。通过“问题串”逐步引领，深度挖掘反比例函数图像的应用，重构关联知识，培养学生数形结合的数学思想，提高学生对知识的综合应用能力。

六、反馈与评价

深度学习的效果如何要借助教学的反馈与评价来实现，不能认为让学生做难题就是进行深度学习，而是要让在一层层深入研究的过程中教师的教学水平得到提升，学生的学习能力得到锻炼与提升，培养学生不怕困难的坚韧毅力，培养学生打破砂锅问到底的精神，而这些能力也正是新时代强调的学生的核心素养，这为学生今后挑战高难度的学习打下良好的基础，所以在学校推行深度学习的过程中，我校数学组形成了一系列的教学课堂评价体系，也探索出在小组合作教学这一高效的组织形式下，如何更有效地培养学生的数学素养。