周期性往复运动中的几种单停止运动规律

姜 华

（上海旭恒精工机械制造有限公司，上海 201814）

0 引言

往复运动是一种常见的运动形式，具有周期性强、机构占用空间少、运动精度高等优点，从而广泛应用在各种印刷、包装机械中[1]。因往复运动自身的原因，它同时还具速度不均匀、稳定性差、冲击性强等缺点，导致机构在高速时经常会出现定位不准、运行抖动等问题。刘晓敏等采用不完全齿轮和齿条研制了一种等速无冲击直线往复运动机构，该机构可以实现等速直线往复运动且行程不受限制[2]。陈宇等提出了一种利用非圆齿轮机构与正弦机构串联组合的机构，可以严格实现从动件等速往复运动规律[3]。唐文艳等基于可拓学的可拓策略生成方法设计了刨床刨刀往复运动机构[4]。然而以上机构结构比较复杂，凸轮机构具有结构简单、工作可靠、便于控制等特点[5-6]，可以快速实现往复运动。不同运动规律的凸轮曲线其动态性能差异较大[7-8]，在满足工作要求的条件下，设计出合适的运动规律对于改善运动性能至关重要[9]。虽然凸轮曲线的设计理论已较为成熟，但许多包装机械单位不能根据自己的实际情况科学地加以应用[10]。根据实际工程中单停止往复运动的要求，文中分别利用多项式和谐波函数分析设计了3种运动规律，均可满足工程应用，其中 4-5-6-7-8多项式单停运动规律的综合性能较好。

1 单停止往复运动

所谓单停止往复运动，是指在往复运动的2个端点中，运动在其中一个端点没有停留，仅作为折返点，而另一个端点是停留点，停留时间可根据工况需求来设定。一般情况下在停留点停留时间段的起、停时刻，运动所承受的负载会有较大的变化，而在折返点负载的变化会较小或没有变化。如周期（间歇）性往复定位机构，定位动作是在停留时间段内完成的，定位和定位释放均会产生负载变化，而另一端只是返回过程，没有增加或减少额外的负载。为减少在停留点起、停时刻的运动冲击，提高运动稳定性，要求或希望在起、停时刻的速度（V）、加速度（A）、跃度（J）均要为零；而在折返点是把起、停时刻合并为一个时刻，可以称为转向时刻，只需要满足速度（V）为零，而加速度（A）和跃度（J）可以不需要为零。这就是单停止往复运动和一般双停止往复运动的最大区别。

2 单停止往复运动规律的函数及曲线

根据单停止往复运动的特性，本文选择3种运动规律的函数及曲线来进行解析。

2.1 采用双停运动规律来合成单停运动规律

双停运动规律有很多，常用的有正弦（摆线）加速度运动规律、修正正弦加速度运动规律、梯形加速度运动规律、修正梯形加速度运动规律、多项式（3-4-5，4-5-6-7）运动规律等，各自的特性也不相同。这里选择在运动的起点和终点的跃度（J）均为零的 4-5-6-7多项式运动规律来合成一个单停运动规律，求解出SVAJ的函数表达式并做出图形。

根据双停运动要求设定边界条件。B为升程运行时间（此处按半周期180分度计算）；时间T=0时：S=0；V=0；A=0；J=0；T=B时：S=1；V=0；A=0；J=0。

可求解出升程运动的 4-5-6-7多项式运动规律的SVAJ函数表达式为

回程运动规律如下：

根据升、回程运动规律的函数表达式，做出如下SVAJ函数曲线图（图1）。从图1中可以看出在中间折返点，加速度出现了一次不必要的回零，从而造成了跃度曲线的一次额外波动（图1中A和B这2个波峰）。但所有曲线都是连续的，说明这是一种可以接受的运动规律。

2.2 采用二个不同周期的谐波函数合成单停运动规律的函数

根据单停止往复运动在折返点加速度可以不为零的特点，其加速度函数可以利用周期性谐波函数来合成，如图2所示，利用一个半周期谐波函数和一个全周期谐波函数相叠加，得到一个新的双谐波函数，合成前的2个谐波函数的振幅是相同的，合成后新的双谐波函数就可以满足起点加速度为零而折返点加速度不为零的要求。

因此，先设定所求升程加速度的函数为：

式中：B为升程运行时间（此处按半周期 180分度计算）；T为时间，T=[0～B]。

对上述加速度函数积分得速度的函数式为

图1 4-5-6-7多项式函数运动规律曲线图

图2 双谐波函数合成示意图

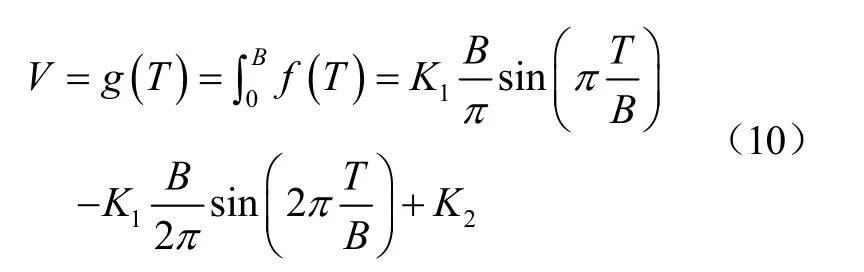
同理得位移函数为

根据单停运动要求设定边界条件，T=0时，S=0，V=0，A=0；T=B时，S=1，V=0。

可解得双谐波单停运动中升程运动规律的函数表达式为

采用上述相同的方法，得回程运动规律的函数表达式为

根据双谐波单停运动升、回程运动规律的函数表达式，绘出SVAJ函数曲线图（图3）。从图中可以看出，在曲线的中间折返点处，加速度没有回零，减小了跃度曲线的一次波动，所有的曲线都是连续的，也是一种可以接受的运动规律。相对于2.1的加速度曲线，最大加速度值会略高一些（图4）。

图3 双谐波函数运动规律曲线图

图4 加速度曲线对比图

2.3 利用边界条件计算出的多项式单停运动规律

单停往复运动可以描述成：起动→折返→停止，以整个运动过程做为研究对象，设立边界条件（B为升、回程总运动时间，此处按全周期360分度计算）：时间T=0时，S=0，V=0，A=0，J=0；时，S=1；T=B时，S=0，V=0，A=0，J=0。

建立S、V、A、J函数表达式为

式中：T为时间，T=[0～B]。

根据边界条件，利用Matlab等解算软件，可得多项式单停往复运动规律的函数表达式为

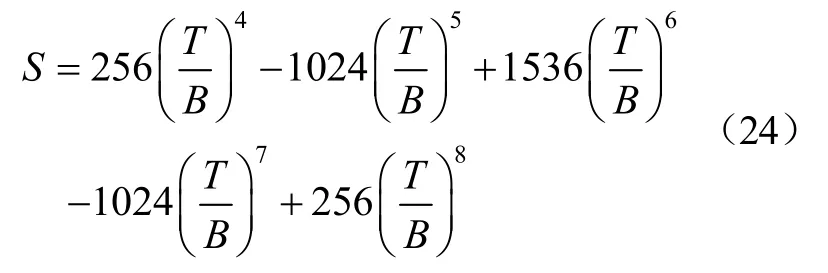
按上述位移函数中各项的指数，此组函数可称为4-5-6-7-8多项式单停运动规律，绘出SVAJ函数曲线图（图5）。从图中可以看出，同2.2双谐波函数一样，在曲线的中间折返点处，加速度没有回零，同2.1函数曲线相比，跃度曲线减小了一次波动；所有的曲线都是连续的；最大加速度和2.1函数曲线的最大加速度接近（图4）；最大速度比2.1和2.2函数曲线的最大速度都略低一些（图6）；是一种较好的单停往复运动规律。

3 三种运动规律的特性值计算及分析

无纲量运动参数中的最大速度、最大加速度、最大跃度和最大惯性距（同一时刻速度和加速度的乘积），称为运动规律的特性值，分别用Vm、Am、Jm、Qm表示。通过这些特性值，可以了解运动规律所适合的运动（工况）条件，没有任何一种运动规律所有的特性值都是最低的，所以在不同的工况条件下需要选择不同的运动规律，如高速运动的机构选择加速度较小的运动规律，负载较重时选择速度较小的运动规律等，这些在许多文献内均有详细说明。

通过SVAJ曲线可以看出，各特性值均是所在曲线的一个极值点，只需得到曲线上该极值点的横坐标，代入相关函数式即可。极值点处的一阶导数为零，所以很容易得到该极值点的横坐标。以计算4-5-6-7-8多项式单停运动规律的最大跃度为例如下：

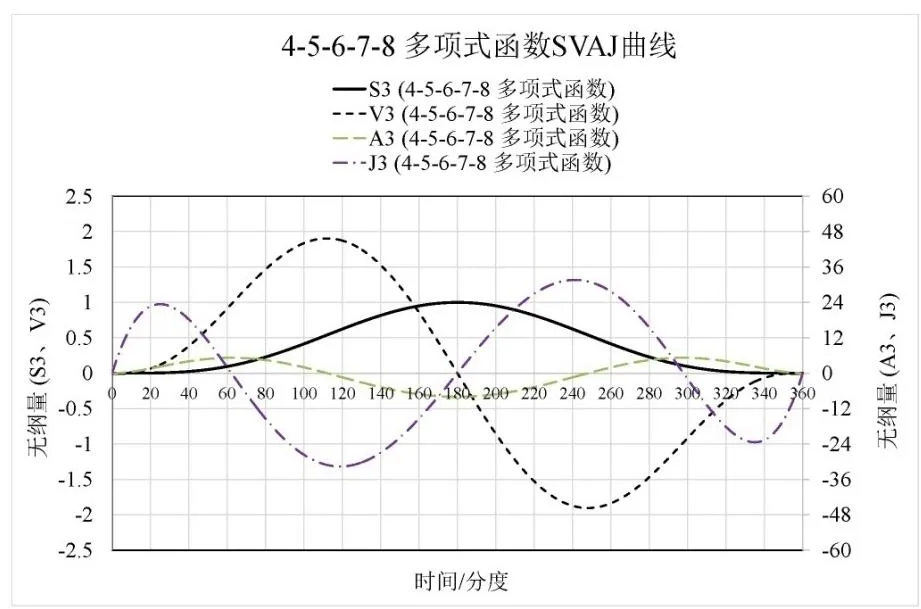
图5 4-5-6-7-8 多项式运动规律曲线图

当j=0时可求出跃度曲线的极值点横坐标值。

分别代入无纲量跃度计算式后得4个值，其中绝对值最大的是 4-5-6-7-8多项式单停运动规律的最大跃度特性值：

Jm=±31.6207

根据同样方法，计算出上述3种运动规律的特性值见表1。

图6～图8是把3种运动规律的特性进行横向比较，从中不难看出4-5-6-7-8多项式运动规律的特征值的绝对值最小，则机构实际运行过程中所承受的直接冲击和柔性冲击在此3种运动规律中也是最小的可以使往复运动更加平稳。设计出的4-5-6-7-8多项式运动规律曲线应用在自己的实际工程中，且效果很好，各项参数优异，是文中的核心和创新，而凸轮曲线运动规律的设计问题是个无休止问题，可能还存在比4-5-6-7-8多项式参数更好的曲线A，后面还会设计出比A好的B，但是设计的复杂性极具增加，或许没有必要。

表1 特性值对照表

图6 速度曲线对比图

图7 跃度曲线对比图

图8 惯性距曲线对比图

4 结论

解析了3种单停止往复运动规律，利用单停往复运动在折返点加速度可以不为零的特点，可以减少跃度曲线的波动，降低运动规律的特性值，从而设计出4-5-6-7-8多项式单停运动规律。这种运动规律具有较好的动态性能，在满足工程应用的同时可以减小冲击，保证机构平稳运行。此外，单停曲线的最大加（减）速度经常是出现在折返点处，折返点一般情况下也是运动的最远点，所以这种特性对于弹簧复位的机构充分利用弹簧的性能是有利的，可以较大幅度提升机构的效率。

样条曲线的世界丰富多彩，这里仅撷取几片浪花加以赏析，在实际运用时需同运动条件加以匹配，充分考虑载荷、时间、空间、成本等因素，不要单纯套路一些固定公式，适合的，才是最合理的、最美妙的机械运动。