基于模糊FMECA的克令吊可靠性分析

叶 凯，蔡 冲，陆兆鹏

（武汉船用机械有限责任公司，武汉 430084）

0 引言

典型的机电系统通常包含机械系统、液压系统、电气系统和软件系统，具有“机”和“电”的双重属性。机械系统通常由运动零部件和静态零部件组成。动态零部件通常以损耗失效为主要故障模式，而静态零部件的故障模式则取决于其维护情况、工作特点以及使用环境等因素，进行可靠性预测具有很大难度。另一方面，机械系统中的大部分零件往往为某类设备专门设计，相较于电子元器件标准化程度低，数据难以积累，造成同类零件也无法形成统一的可靠性数据。

目前，FMECA已成为国内外可靠性工程领域中解决非电子产品的成熟而有效的设计分析方法，并得到广泛的重视和应用。

1 基于模糊FMECA的机电系统可靠性分析

1.1 FMECA介绍

FMECA（Failure Mode Effect and Criticality Analysis，故障模式影响及其危害度分析）是一种归纳分析方法。它通过分析系统中每一种零部件可能出现的所有故障模式及对系统造成的相关影响，按照每种故障模式的发生概率、严重程度、检测难易以及维修难易等多个维度进行综合分析，为系统可靠性评价和设计改进提供基本信息，通过消除潜在故障或降低其损失，达到提高系统安全性和可靠性的目的。

FMECA是按照一定的格式和步骤，分析每一个部件（功能）可能有的失效模式，以及对系统的影响，后果的严重程度。由于FMECA涉及的问题广泛，需要由十分熟悉产品情况的设计人员经过充分的调查研究以后做出分析，并由其他专业人员予以协助。

1.2 基于模糊FMECA的机电系统可靠性分析

典型的FMECA是一种常用的系统可靠性分析方法，使用时要求界限划分明确，便于进行定量分析。但对于复杂的机电系统而言，往往需要借助相关技术人员丰富的工程经验，将模糊指标定量化，从而完成FMECA。

针对上述问题，目前已有很多学者和工程研究人员将模糊理论与FMECA分析方法相结合，对系统可靠性进行研究和综合评估。

模糊FMECA的基本流程图如图1所示。

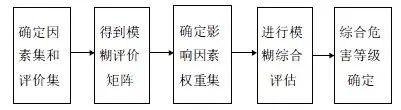
图1 模糊FMECA的基本流程图

1）确定因素集

故障模式k评价分析的因素集可以表示为

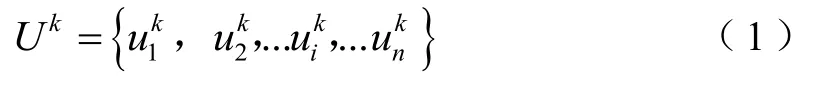
式中：ui为故障模式k的第i个影响因素。

2）确定评价集

评价集是由对评价对象可能做出的评价结果所组成的集合。

式中：m为评价分级数；vj表示第j个评价等级。

3）建立模糊评价矩阵

成立一个由h人组成的专家评价组，每位专家对各影响因素给定唯一评价等级vj。若h位组员中评定隶属于vj的有人，则的评价集为

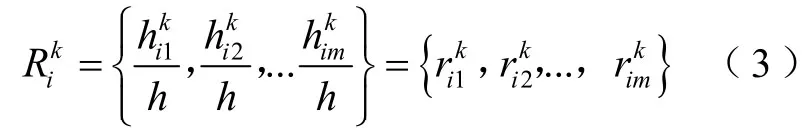
故障模式k模糊因素水平评价矩阵为

4）建立影响因素权重集

5）一级模糊综合评估

将故障模式k的因素权重集改写为向量形式。则：

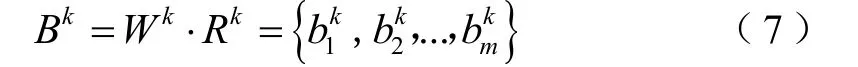
Bk为故障模式k的模糊综合评价向量。

6）确定综合危害等级

通过加权平均法对Bk进行处理，得到评价结果：

由此得到各故障模式的综合危害度等级的集合：

2 基于模糊FMECA的克令吊可靠性分析

2.1 克令吊FMEA分析

克令吊是一种配套在普通货船、集装箱船、散货船和其他运输船上的甲板起重设备。按照动力来源，主要分为电动液压克令吊和纯电动克令吊。其中，电动液压克令吊技术更加成熟，配套更为广泛。

以某型电动液压克令吊为分析对象。该型克令吊由机械系统、电气系统和液压系统组成，能够实现货物升降、变幅和吊机360°回转的功能。

参照《Q/HJB100-004.8-2015甲板机械故障模式影响及危害性分析（FMECA）通则》对该型令吊进行故障模式及影响分析（FMEA）。基本步骤如图2所示。

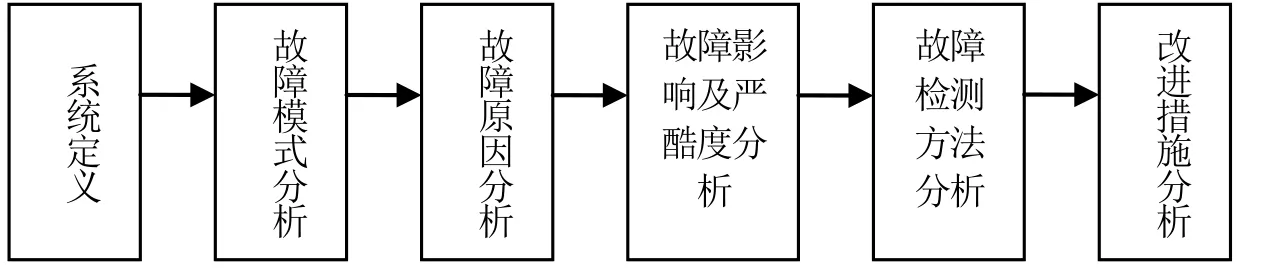
图2 FMEA一般流程图

根据该型克令吊近10年的售后保单情况，梳理筛选故障类型，得到吊机机械系统、电气系统和液压系统FMEA表。如表1所示。

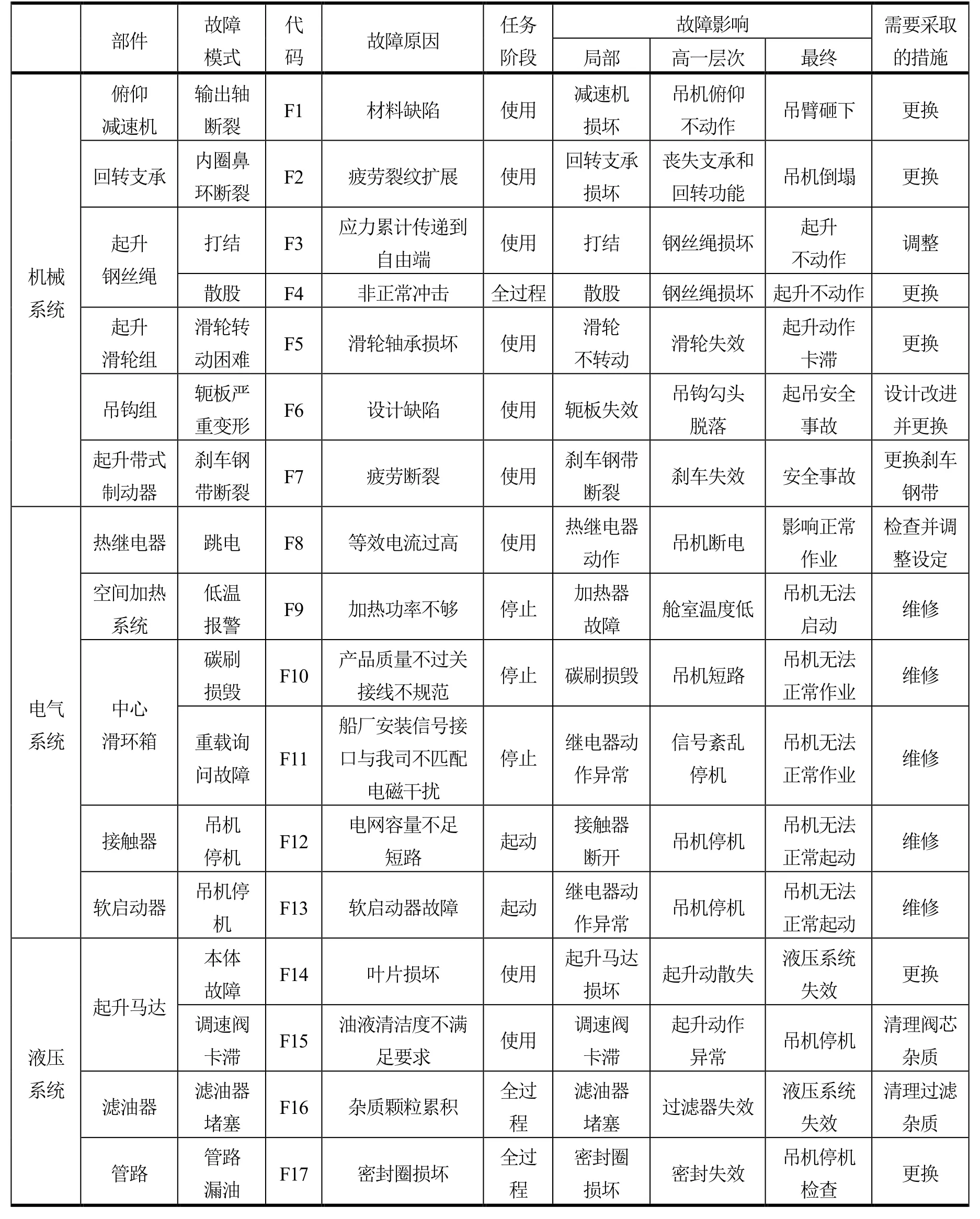
表1 克令吊FMEA表

2.2 基于模糊FMECA的克令吊可靠性分析

常见的电动液压克令吊主要包括机械系统、电气系统和液压系统，是一类典型的机电系统，难以通过简单的定量分析和定性判断，完成其可靠性评价，从而对设备使用和维护保养做出针对性指导。因此，需要借助模糊FMECA方法进行分析。

过程如下：

1）建立因素集

根据因素水平等级表，建立因素集为

U={故障概率等级，严重度等级，检测难易程度等级，维修难易程度等级}

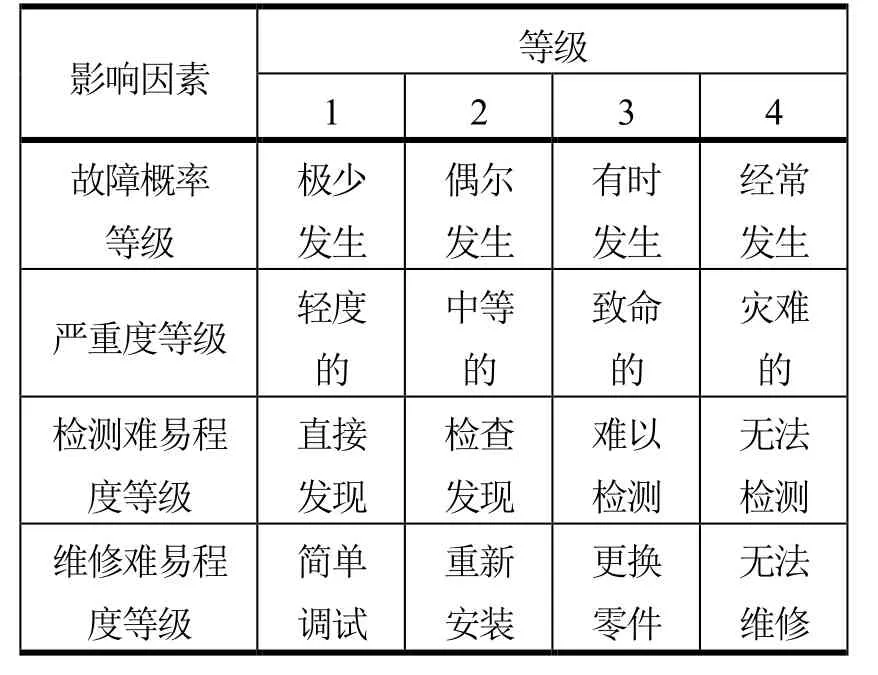
表2 因素水平等级表

2）建立评价集

如上可知，评价集为

V={1,2,3,4}

3）建立故障模式的模糊评价矩阵

同样地，其他故障模式的模糊评价矩阵分别为

4）确定权重集

用aij表示影响因素对于的相对重要数值，构造判断矩阵。

将判断矩阵A的各行向量进行几何平均，然后归一化，得到排序权重向量。计算步骤如下。

（1）计算判断矩阵A各行元素乘积的n次方根

（2）对向量M归一化

（3）计算判断矩阵A的最大特征值

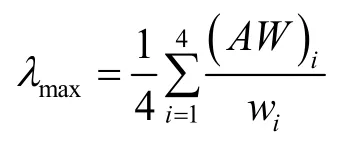
式中：(AW)i为AW的第i个分量。

计算出判断矩阵的最大特征根λmax及其所对应的特征向量之后，在进行一致性检验，计算一致性比率Rc为

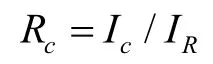
式中：Ic为一致性指标，Ic=（λmax-n）（/n-1）；IR为判断矩阵的平均随机一致性指标，通过查找文献得知，当n=3时，IR=0.58；当n=4时，IR=0.90；当n=5时，IR=1.12；当Rc＜0.1时，认为判断矩阵的一致性是可以接受的。

故障F1的判断矩阵为

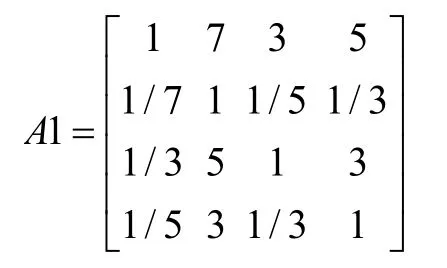
其权重向量为

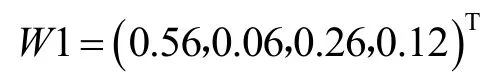
判断矩阵A的最大特征值：

λmax=4.129

一致性指标：Ic=0.043，Rc=0.048

因此故障模式F1因素集对应的权重向量为

同理，其余故障模式因素集对应判断矩阵和权重向量如下：

表3 因素重要程度判断值表

5）一级模糊综合评估

根据式（8），确定极地甲板吊机各故障模式的模糊综合评价向量如下：

B1=(0.56, 0.176, 0.26, 0.26)

B2=(0.56, 0.12, 0.16, 0.26)

B3=(0.342, 0.246, 0.15, 0.27)

B4=(0.476, 0.228, 0.366, 0.06)

B5=(0.184, 0.286, 0.167, 0.07)

B6=(0.33, 0.068, 0.348, 0.05)

B7=(0.56, 0.232, 0.46, 0.26)

B8=(0.333, 0.375, 0.27, 0.27)

B9=(0.57, 0.172, 0.57, 0.12)

B10=(0.348, 0.276, 0.42, 0.12)

B11=(0.126, 0.158, 0.294, 0.228)

B12=(0.48, 0.227, 0.404, 0.136)

B13=(0.461, 0.164, 0.2671, 0.328)

B14=(0.441, 0.146, 0.09, 0.16)

B15=(0.337, 0.379, 0.47, 0.415)

B16=(0.318, 0.415, 0.47, 0.432)

B17=(0.318, 0.356, 0.299, 0.434)

6）综合危害等级的确定

通过式（9），得到极地甲板吊机各故障模式的综合危害度等级集合为

数值大小即是各故障模式危险度综合评价结果。

7）多级模糊综合评价

由于本分析过程中故障模式的选取并未按照系统组成逐级划分，因此无须进行多级模糊评价。

3 结论

模糊FMECA能够有效解决机电系统中机械部分故障往往难以精确描述但不能忽略的实际情况。尽管组成克令吊的机械系统、电气系统和液压系统，在该类产品上具有较为成熟的应用，但利用模糊FMECA进行可靠性分析的过程中，因素集的选取、专家意见的收集情况，对最终的分析评价结果有很大影响。因此，后续分析中，细化因素集的划分，扩大专家意见收集范围，有助于得到更为准确、合理的故障模式危险度综合评价结果。

另一方面，通过对大量实际使用数据的跟踪收集，可以实现对模糊评价结果的对照检查，从而对分析过程中的模糊参数进行可靠量化，提高分析的准确性。