简论高中数学教学中数形结合的方法应用

靳鹤云

(新疆疏勒县八一中学 新疆 喀什 844200)

1.数形结合思想内涵

数形结合思想是数学教学中一个重要的数学思想，对解答高中抽象的复杂的数学问题尤为重要，其内涵是：通过数与形之间相互转化，对抽象复杂的数学问题进行解答的过程。数形结合思想的应用包含了两种情况：一是“以形助数”。抽象的数学概念，复杂的数量关系，借助图形使之直观、形象、简单。在解题中常常借助图形的直观性帮助分析数量关系。高中数学教学常常用到的有：数轴、Venn图、单位圆，函数图像，算法流程图等。二是“以数解形”。借助数学推理，使有“形”的数学问题量化，从而准确揭示“形”性质。数学结合的数学思想，是解决数学问题的极佳手段。它是数学知识和能力融合。应用数形结合思想，能帮助学生形成数形结合的思维形式，激发学生的学习欲望，提高学生的解题速度，提升学生的数学素养和思维能力，提高课堂教学质量。

2.数形结合思想在高中数学教学中的应用分析

2.1 在集合教学中的应用。教学高中数学集合这个内容中，如果能以数形结合的思想为指导，借助图形进行思考，不仅可以使各集合之间的相互关系直观明了，而且更便于将各元素的归属确定下来，使抽象的集合问题通过直观的形象思维得到解决。如：在研究集合与集合的关系时，让学生熟练运用Venn图，在进行集合间的运算时，可以将题设通过数轴表示，这样既易于理解，又能提高解题的准确性；在集合中，求参数a的取值范围时，首先需要建立关于a的不等式，通过数轴表示解的集合，进而求得参数a的取值范围。再如：为了体验Venn图的直观、简便，教师在教集合时可以出这样的问题：在秋季校运会中，某班有28个同学参加比赛，有15人参加径赛，有8人参加田赛，有14人参加球类比赛，同时参加田赛和径赛的有3人，同时参加径赛和球赛的有3人，没有同时参加三项比赛的同学，则同时参加田赛和球类比赛的有多少人？只参加径赛的同学有多少人？这道题，涉及到集合与集合的关系，集合之间的运算，教师要指导学生把文字转化成集合语言，用集合符号表示他们之间的关系，把全班参加参赛人数用全集U表示，设参加径赛的集合为A,参加田赛的集合为B，参加球类比赛的集合为C，同时参加田赛和球类比赛的有x人。然后根据题意画出Venn图。在图上适当的位置进行填数和计算，这样把复杂的语言变成直观图形，使抽象的集合问题通过直观的形象思维得到解决。

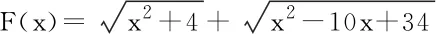
2.3 在解三角形中的应用。解三角形是高中数学重要内容，本章实际应用较多，解题关键就是将实际问题数学化。数形结合思想是解决这个关键的指导思想，根据题意画出示意图，将已知条件的长度、角度，转化成三角形相对应的边和角，把实际问题转化为解直角三角形的问题，这样将抽象问题具体化、形象化，使问题易懂，易于解决。如：如某人从塔的正东沿着南偏西60度的方向，前进40米后，看见塔在东北方向，若沿途测得塔的最大仰角为30度，求塔高。不借助图形，很难解答。根据条件设塔高为AE，B为塔的正东方向的一点，某人沿南偏西60度的方向前进40米到达C处，BC=40米，且

2.4 在三角函数中的应用。数形结合思想是处理三角函数有关问题的重要思想方法，在解决三角函数有关问题时，关键是代数问题与图形之间的互相转化，它可以使代数问题几何化，几何问题代数化。如在求函数解析式定义域时，可以建立使函数有意义的不等式组，再建立直角坐标系，结合单位圆中正弦线和余弦线求解；在求方程解的个数问题时，有时候如果无法求出方程的解，一般构建两个函数转化为研究两函数图像的交点个数问题求解；求方程中参数的范围问题，可利用三角函数的图像和性质确定参数的取值范围；求三角函数的最值问题，对于比较容易画出图像的函数，可借助图像直观的求出最值。

综上所述，在高中数学课堂应用数形结合方法，可以帮助学生提高分析问题、解决问题的能力，提升数学品质，为今后的发展奠定基础。