深水救援井动态压井参数优化设计方法*
2020-08-03孙长利苗典远李允智王福学
孙长利 苗典远 李允智 王福学 张 帅
(中海油能源发展股份有限公司工程技术分公司 天津 300452)
随着陆地油气资源的不断开采,全球能源勘探开发正逐步过渡到海洋深水区域。深水油气开发的最显著特点是高风险[1-2],一旦井喷失控,就会造成严重环境灾难和巨大经济损失。当深水钻井过程中一、二级井控失效时,救援井压井方法成为解决井喷事故的关键手段[3]。2010年墨西哥湾井喷事故发生之后,诸多石油公司和政府要求进行深水钻井作业之前,必须具备完善的救援井压井设计方案[4-5]。
救援井是与事故井连通的定向井[6],通过向事故井注入大排量、高密度的压井液,实现抑制井喷的目的。救援井动态压井设计的关键是事故井连通之后的井筒压力计算。为解决动态压井过程中井底压力计算问题,国内外学者进行了大量的基础理论研究。Warriner[7]提出单相液柱纯摩阻计算模型,该模型假设已经压井成功,利用纯液柱压力和摩阻来平衡地层压力;1996年,Abel[8]提出了动态压井计算的稳态与非稳态两相流模型,将气液两相流理论应用到动态压井中;金业权等[9]指出动态压井法应受地层压力和现场压井泵组的限制,并根据地层压力和地层破裂压力,给出了动态压井可行判别式,动态压井设计思路与Warriner[7]一致。邓大伟等[10]提出了利用单相流模型、稳态和瞬态两相流模型确定动态压井排量。除了单相流体摩阻模型外,至今未有公开的多相流动态压井模型及其算法。
本文综合考虑连通点处压井液下落判别模型、连通点以下的零表观液速流井筒压力计算模型、连通点以上井筒多相流动模型,建立了直接连通方式下救援井动态压井模型。通过实际井身结构数据进行压井过程模拟,并对不同压井参数条件下的模型计算结果进行了分析,以期为深水救援井动态压井设计提供参考。
1 连计通算点方以法下气液两相流动关键参数
1.1 临界携液气速
临界携液气速是指液滴无法被携带并回流到气芯中的气体流速。压井过程中,若井筒内的气体速度大于临界携液气速,则压井液被高速气流携带,无法在连通点处下落;当井筒内的气体流动小于临界携液气速时,压井液在连通点处发生下落并回流到连通点以下的井段。因此,判断是否能够压井成功,关键是连通点处临界携液气速的计算。
压井液在高速气流中破裂形成液滴是个复杂气相动力学和水动力学的过程[11]。本文假定液滴为圆球形,压井液液滴在气芯中的受力情况如图1所示,受力主要包括重力、浮力和拖曳力。液滴受力情况与气体流速、液滴直径、液体密度、表面张力相关,因此对液滴运动情况判断时需要建立压井液在运动方向上的力学模型。
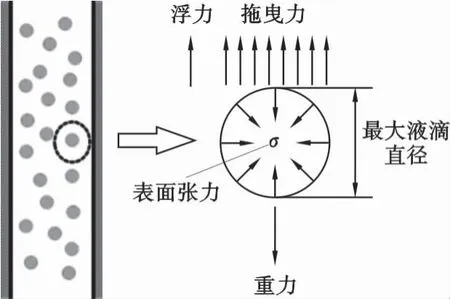
图1 井筒中液滴受力模型示意图Fig.1 Schematic diagram of force model of droplets in wellbore
在运动方向上,液滴所受的拖曳力计算模型为[12]

液滴所受重力为[12]

液滴所受浮力为[12]
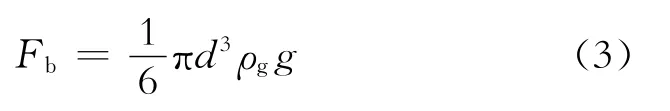
式(1)~(3)中:Fd为液滴受到的拖曳力,N;Fg为液滴受到的重力,N;Fb为液滴受到的浮力,N;d为液滴半径,m;g为重力加速度,m/s2;ρl、ρg为液滴和气体的密度,kg/m3;Cd为拖曳力系数,无因次;vg为气体实际流速,m/s。
结合牛顿第二定律与液滴受力分析,可以建立如下液滴在气芯中的运动速度模型[12]:

当液滴在气芯中达到终速度时,方程(4)中时间项为零,液滴的重力与浮力和垂向上拖曳力达到平衡状态,此时得到的气相速度即为当前条件下的临界携液气速[12],模型由式(5)给出。
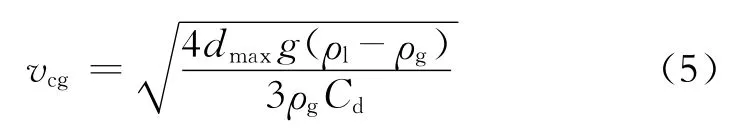
式(4)、(5)中:v为液滴的速度,m/s;t为时间,s;vcg为临界携液气速,m/s;dmax为最大液滴直径,m。
由式(5)可以看出,临界气速受液滴直径以及拖曳力系数影响,液滴直径越大,临界携液气速计算值越大,因此计算临界携液气速的关键是求解最大液滴直径。液滴最大直径计算模型见表1。Flores[15]通过一口849 m的试验井对表1模型进行了评价,实验临界携液气速为5.97 m/s,4种模型计算结果分别为5.66、2.83、3.01和10.96 m/s。由此可见,Turner模型计算结果与实验临界携液气速最为接近,可较为准确地预测压井液下落的临界气速。
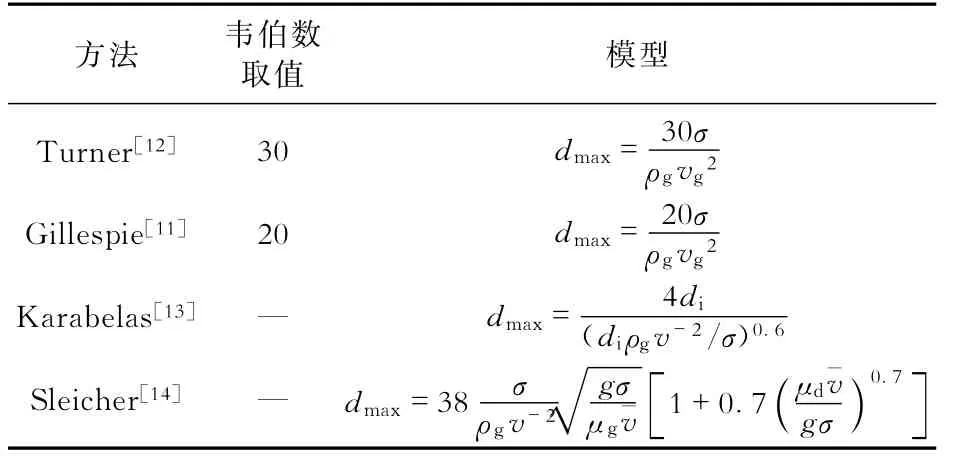
表1 液滴最大直径计算模型Table 1 Calculating model of maximum droplet diameter
将表1中Turner最大液滴直径预测模型代入式(5),可以得到临界携液气速模型

式(6)中:σ为表面张力,N/m。表面张力σ主要受温度和压力的影响,在井筒中压井液液滴的表面张力计算参照式(7)~(9)[16]

式(7)~(9)中:p为压力,MPa;T为温度,K。
式(6)中液滴拖曳力系数的求取方法包括图版法和公式法,由于图版法不适合计算机编程求取,因此本文选取公式法进行计算。邵明望等[17]通过对大量的实验数据采用非线性拟合,整理得到适合于全流型范围的高精度拖曳力计算公式,液滴拖曳力系数由式(10)计算。
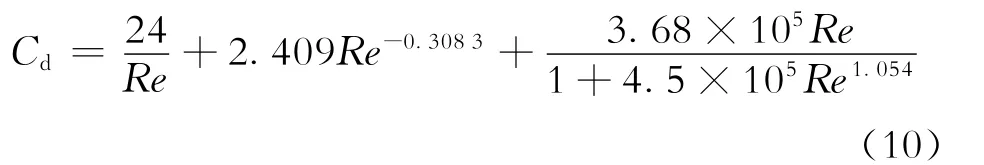
式(10)中:Re为雷诺数,无量纲。
将式(7)~(10)代入式(6)中,即可得到不同深度处临界携液气速模型。
1.2 零表观液速流流型转化判据
压井过程中,随着连通点以上液柱的逐渐建立,井底压力逐渐增加,井底产气量减小,在连通点处气体流速最终小于临界携液气速,压井液发生下落,在裸眼段形成气液两相流。而在井底边界处液相表观流速为零,在连通点以下的裸眼段逐渐积累形成零表观液速流。零表观液速流的传质传热特性不同于常规气液两相流,常规的流型划分判别条件不再适用,为保证井筒内压力计算的准确性,需要引入零表观液速流流型判别条件。
Zhang等[18]通过对零表观液速流理论分析建立了零表观液速流流型划分模型,通过实验验证该模型能够准确预测零表观液速条件下的流型,并通过模型对比指出该模型计算精度高于其他流型划分模型。
1)泡状流-段塞流转化判据。
泡状流流动条件下由于管壁的影响,管中心的气泡速度高于管壁处的气泡速度,当管中心气泡的速度大于Taylor泡的速度时,气泡将会在管壁中心发生聚并,气泡也会发展为Taylor泡,此时泡状流转化为段塞流[18]。
泡状流条件下,管中心位置处的气泡速度为

段塞流条件下,Taylor泡的上升速度为
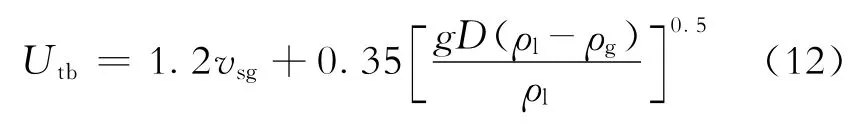

当Ubc≥Utb时,流型将由泡状流转化为段塞流,由此可以得到流型转化条件
式(11)~(13)中:Ubc为管中心位置处的气泡速度,m/s;Utb为Taylor泡上升速度,m/s;vsg为气体表观速度,m/s;D为当量直径,m。
2)段塞流-搅动流转化判据。
段塞流流动条件下,Taylor泡尾流长度与气泡的速度相关,随着气泡速度的增加,尾流长度增加,尾流强度增加。随着尾流强度增加,被扰动液塞长度增加,当整个液塞段全部被扰动时,段塞流转化为搅动流[18]。
段塞流流动中尾流长度的计算模型为
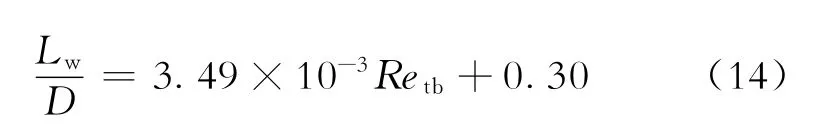
式(14)中:Retb为Taylor泡雷诺数;Lw为尾流长度,m。
液塞长度Ls通过气液相的连续性方程及其辅助方程求解,段塞流条件下气液相的连续性方程为

式(15)、(16)中:Us为液塞平均上升速度,m/s;Ls为液塞长度,m;Ltb为泡的长度,m;Lu为段塞总长度,m;Hgtb为Taylor泡区域的空隙率,无量纲;Hgs为液塞区域的空隙率,无量纲;Ulf为液膜平均速度,m/s。
3)搅动流-环状流判别条件。
环状流形成不受液相流速的影响,其判别条件为[18]
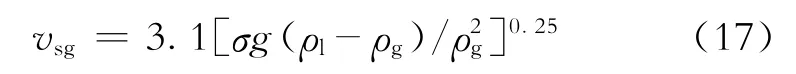
1.3 井筒多相流动控制方程及求解方法
当压井液通过连通点注入事故井之后,在井筒中形成气液两相流,导致井底压力不断变化,井筒内的气体流量、空隙率等流动参数随时间不断变化,使得井筒流体流动具有非稳态的特性。考虑井筒压力与地层之间的耦合,需要建立非稳态多相流动耦合模型对压井过程进行描述。
1.3.1 多相流动控制方程
漂移流模型被广泛的应用于描述井筒气液两相流动,为描述压井过程,建立井筒多相流控制方程组,作以下流动假设:①流体沿井筒轴向作一维运动;②气相和液相的压力和温度相同;③井筒温度近似等于地层温度;④忽略了气液传质;⑤当压井液开始发生下落后,注入的压井液全部下落到裸眼段中。
针对假设条件⑤,压井液下落到连通点以下的裸眼段中,液相的表观速度为零,摩擦阻力计算结果偏小,因此利用该假设条件设计得到的压井参数更加安全。
基于以上假设条件,漂移通量模型包括3个输运方程,即气体的连续性方程、液体的连续性方程和混合动量守恒方程。事故井井筒中气相的连续性方程分为生产层段和产层以上的非生产段,连续性方程分别由式(18)和式(19)给出、液体的连续性方程由式(20)给出、混合动量方程由式(21)给出。
生产层段气相连续性方程为

非生产层段气相连续性方程为

压井液连续性方程为

混合动量守恒方程为
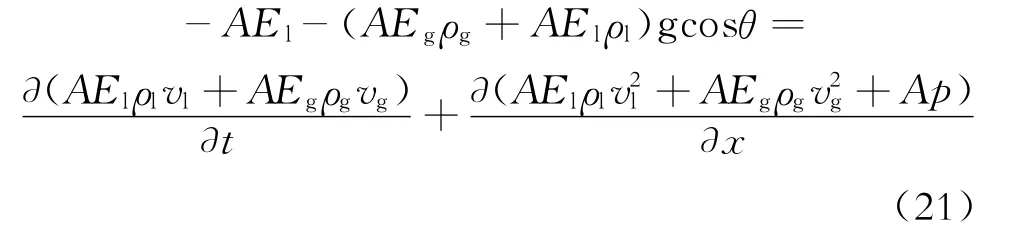
式(18)~(21)中:qg为单位长度储层产气量,kg/(m·s);A为流动通道截面积,m2;θ为井斜角,(°);El、Eg为持液率和空隙率,无量纲;vl为液体的流速,m/s;t为时间位置,s;x为空间位置,m。
1.3.2 定解条件
1)初始条件。
压井之前,事故井已经喷空,井筒内为纯气流。井筒内各点压力、气相密度以及气体流速由气井流入关系曲线(IPR曲线)和井筒内的流出关系曲线(OPR曲线)确定。
初始状态下,井筒内为喷空状态,流体为单相气流,因此有

2)边界条件。
救援井井口为敞喷状态,井口边界条件为井口回压,井筒底部压力等于井底流压,边界条件由式(23)给出。

井底流出边界条件为
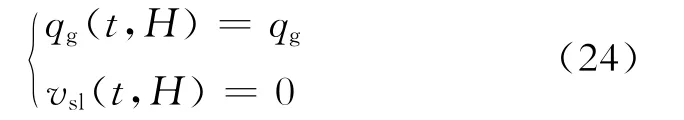
连通点处压井液未发生下落时
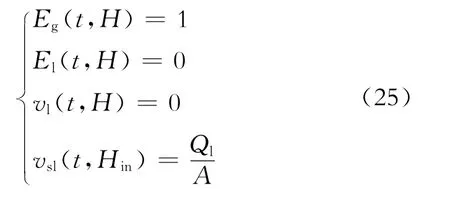
连通点处压井液发生下落时

式(23)~(26)中:qg为井底气体产量,m3/s;pjk为井口回压,Pa;pwf为井底流压,Pa;H为总井深,m;Hin为连通点深度,m;Ql为连通点深度处的压井液排量,m3/s;vsl为液体的表观速度,m/s。
1.3.3 方程离散
本文采用基于交错网格的有限体积法对井筒多相流动模型进行求解。交错网格中在单元中心布置标量变量(压力、空隙、液体密度、气体密度),单元边缘布置矢量变量(液相速度、气体速度)[19]。利用一阶迎风格式对气液两相的动量方程和连续性方程进行离散。
气相连续性方程为

液相连续性方程为
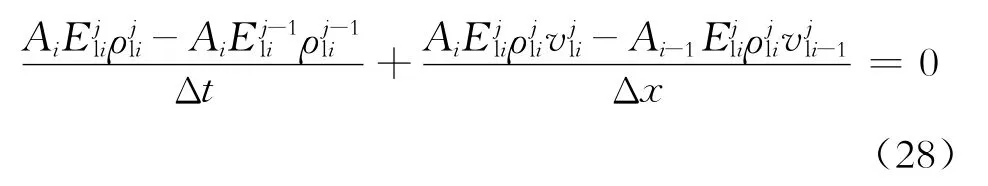
动量方程为
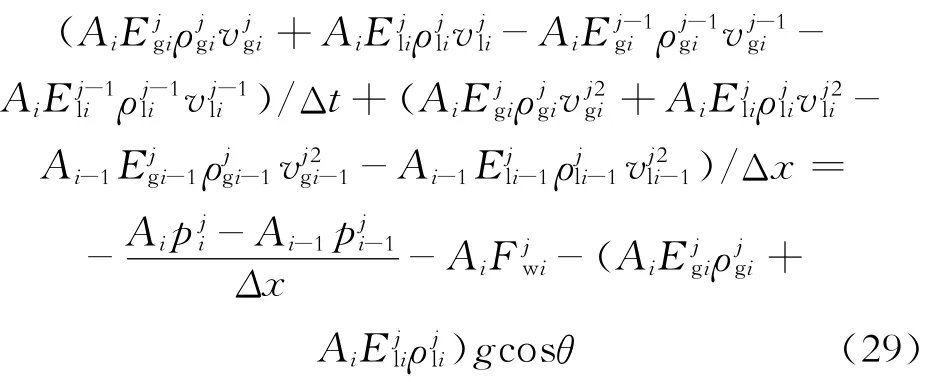
式(27)~(29)中:i、j为单元数;Δt为时间步长,s;Δx为空间步长,m。
1.3.4 辅助方程
连通点以下井段在进行多相流动方程的求解时,需要使用临界携液气速模型和零表观液速流流型转化判据模型作为辅助方程进行求解。
压井过程中连通点以上的井段属于气液共流的流动状态,在求解多相流动方程时,还需要补充多相流动相关的辅助方程。本文在求解多相流动方程时,采用不分流型的漂移流模型,因此辅助方程主要包括:气体滑脱速度计算模型和分布系数模型,分别由式(30)、(31)给出。

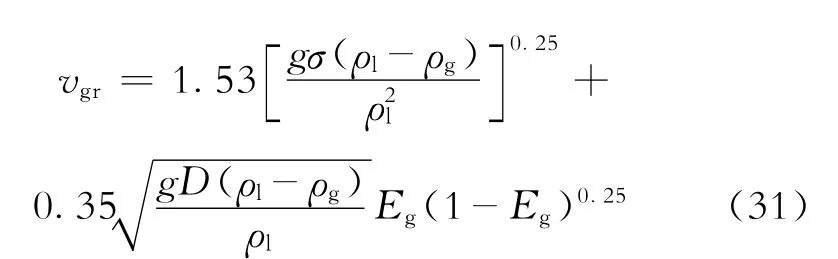
式(30)、(31)中:C0为分布系数,无量纲;vgr为气体的漂移速度,m/s。
1.3.5 求解过程
通过有限差分法对多相流动模型进行离散,将原模型在定解域(空间域、时间域)上的解转化为在定解域上网格节点上的离散解,逐步逐时刻的求解空间域上个节点的解,直到覆盖整个时间域。求解流程图如图2所示,图中n为求解中用来计数的变量,无因次;ts为输入的模拟时间,s。

图2 井底压力计算流程图Fig.2 Flow chart of bottom hole pressure calculation
具体求解步骤如下:
1)设定空间步长dx、时间步长为dt;
2)假定井底空间节点处j+1时刻的压力为
3)利用式(6)计算临界携液气速vcg和产气量
4)判断连通点处压井液是否有下落,并计算裸眼段总压降;
5)对于连通点以上的节点,从连通点处开始算起,假设节点i和i+1的压降为
8)计算节点i+1,i+2,i+3,…,一直计算到井口;
9)若|p(j+1,0)(0)-pwh|<ε(ε为误差精度,pwh为井口回压),则j+1时刻的井底压力为,进行步骤10);否则,重新假设井底流压重复步骤2)~8);
10)计算时刻j+2,j+3,j+4,…,井底压力,直到满足设定的模拟时间ts。
2 方法验证
2.1 与商业软件对比分析
利用本文建立的模型和Drillbench商业软件对1口深水案例井进行了救援井压井过程模拟计算,案例井基本参数见表2,二者计算的井底压力变化规律对比如图3所示。由图3可以看出,压井液排量为250 L/s时,无法压井成功,井底压力较快达到稳定值;压井液排量为333 L/s时能够在井筒内建立完整的液柱,实现成功压井。本文模型与Drillbench软件计算结果趋势一致,结果吻合度较高。
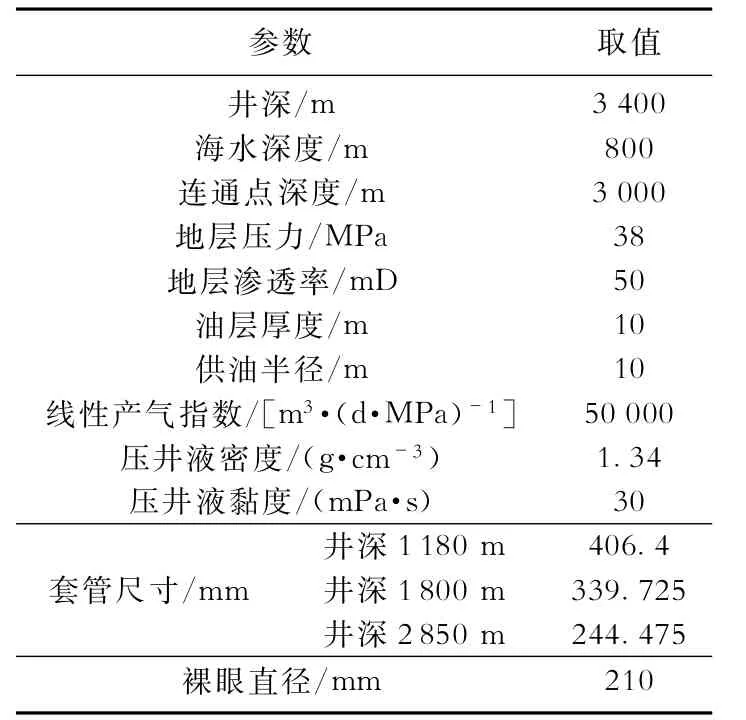
表2 某深水救援井基本参数Table 2 Basic parameters of deep water relief well

图3 本文模型与Drillbench软件计算结果对比分析Fig.3 Comparative analysis of calculation results between the model in this paper and Drillbench software
2.2 与实验数据对比分析
Flores等[15]通过1口测试井对零表观液速流条件下的井筒压力变化规律进行了分析。测试井的基本参数见表3,实验开始前在环空中填充密度为1.04 g/cm3的钻井液,天然气在底深为807 m的油管中注入,在环空中返出。气体由油管流入环空中形成零表观液速流,井底压力由油管底部的压力传感器记录。利用本文模型计算井底压力变化,结果如图4所示。

表3 测试井基本参数Table 3 Basic parameters of test well
由图4可以看出,本文模型计算结果与实验结果趋势一致,与实验结果相比误差均小于15%,能够满足现场井筒压力计算的需求。
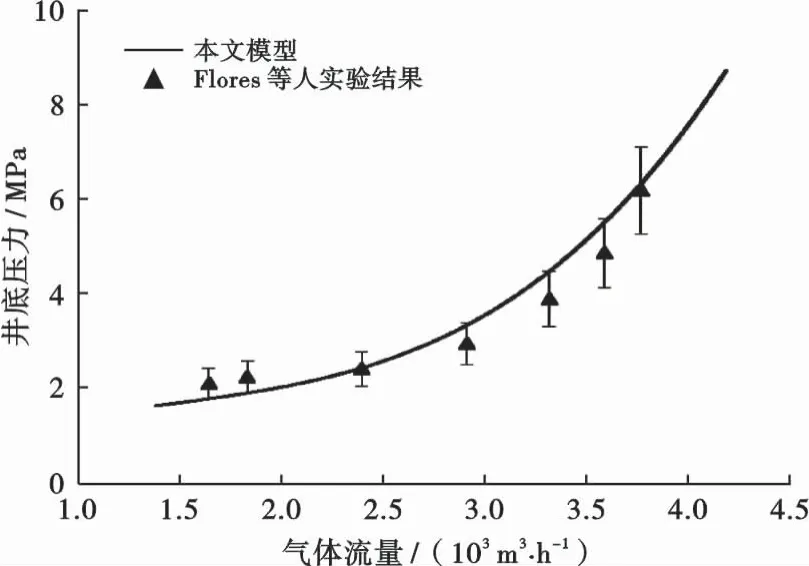
图4 本文模型计算结果与实验数据对比Fig.5 Comparison of results between model calculation and actual values
3 压井规律分析
以南海某井基本数据为例,模拟分析压井规律,该井基本数据见表4。假设钻井过程中发生严重井喷,井内处于喷空状态,救援井的连通点位于事故井井深3 800 m的位置处,通过直接连通的方式进行连通。通过表1参数对压井过程进行模拟计算,并分析了压井排量、压井液密度、压井液流变参数变化对压井结果的影响。
表4 南海某井基本数据Table 4 Basic parameters of a well in South China Sea
3.1 压井液排量影响分析
图5为不同压井液排量条件下压井过程中井底压力和地层产出变化曲线。由图5a可以看出,随着压井液排量增加,井筒内摩阻迅速增加,井底压力逐渐增加。其中压井液排量为60、100和150 L/s时,在连通点处压井液未发生下落,连通点以上快速形成气液两相流,两相流发展稳定之后井底压力不再增加。压井液排量为180 L/s时,在连通点处气速降低到临界携液气速以下时,压井液发生下落。压井液发生下落之后,由于下落量较小,井底压力增长缓慢,当连通点以下的裸眼段被压井液充满时,井底压力仍达不到地层压力,地层仍然产出气体,此时井筒内的气液两相流发展稳定,井底压力不再增加。当压井液排量大于180 L/s时连通点处压井液下落,排量为200 L/s和250 L/s时井底压力高于地层压力,能够压井成功。同时发现,随着压井液排量的增加,压井成功的时间能够缩短。

图5 不同压井液排量条件下井底压力和地层产出变化曲线Fig.5 Bottom-hole pressure and formation production curves under different killing fluid discharge conditions
由图5b可以看出,随着井底压力增加,地层产气量减小;当井底压力高于地层压力时,地层不再产出气体,压井成功。根据图5a得到的随着压井液排量增加压井成功时间缩短的认识,在现场压井泵允许的情况下,可以通过大排量快速压井。
3.2 压井液密度影响分析
图6为不同密度压井液压井过程中井底压力和地层产出变化曲线。由图6a可以看出,压井液密度为1.0、1.1和1.2 g/cm3时,井底压力在短时间内达到稳定,压井液在连通点处未发生下落。由图6b可以看出,随着压井液密度增加,井底产气量降低。当连通点处气体速度小于临界携液速率时,连通点处气体无法继续携带液体向上运移,连通点以下的裸眼段逐渐形成零表观液速流,井底压力继续增加,直至裸眼段被压井液填满,达到稳定状态。裸眼段填满之后,若井底压力低于地层压力时,井筒内发展为稳定的气液两相流,井底压力曲线与密度为1.275 g/cm3的曲线相似;若井底压力高于地层压力,则井底不再产出气体,当井筒内的气体被循环出井筒之后,井筒内发展为单相流,井底压力变化与密度为1.3 g/cm3的曲线相同。随着压井液密度的增加,成功压井时间缩短。
3.3 压井液流变参数影响分析
选取不同流变类型的压井液对压井过程进行模拟,模拟结果如图7所示,其中压井液的流变参数见表5。
由图7a可以看出,宾汉流体流变类型的压井液压井时井底压力增长速率高于牛顿流体的压力增长速率,随着屈服值的增加,宾汉流体的当量黏度增加,井底压力逐渐增加。由图7b可以看出,宾汉流体成功压井时间比牛顿流体压井时间短,这是由于流体屈服值引起的。增加流体的屈服值,导致连通点处压力迅速增加,使连通点处的气体速率提前达到临界携液气速条件,在连通点以下的裸眼段快速形成零表观液速流,实现快速压井。
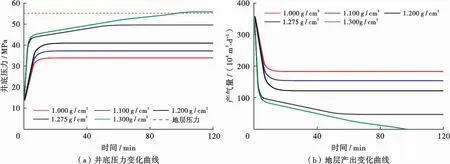
图6 不同密度条件下井底压力和地层产出变化曲线Fig.6 Bottom-hole pressure and stratigraphic output curve sunder different density conditions
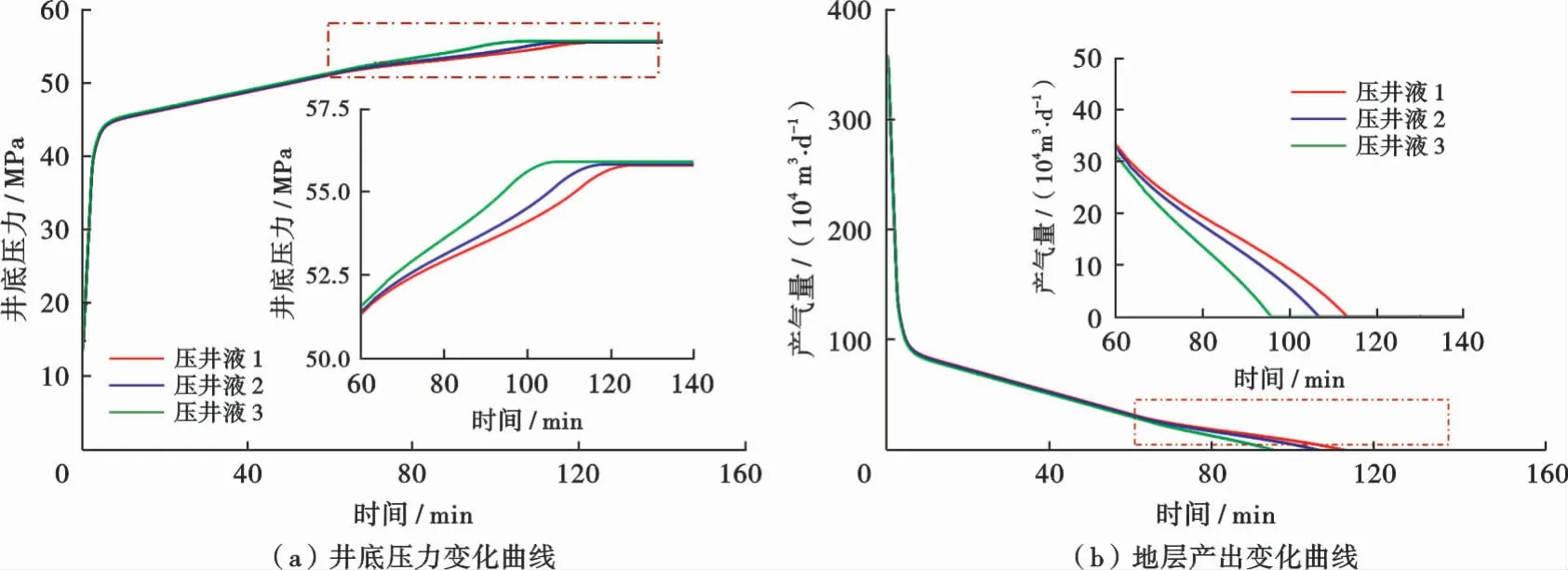
图7 不同压井液流变参数条件下井底压力和地层产出变化曲线Fig.7 Bottom-hole pressure and formation production curves under different rheological parameters of killing fluid

表5 压井液流变参数Table 5 Killing fluid rheological parameters
4 结论
1)基于临界携液气速模型,考虑连通点以下零表观液速流流型判别条件,建立了深水救援井动态压井多相流动模型。
2)模拟计算结果表明,压井过程中井筒内存在3种情况:①低排量低密度时压井液不发生下落,连通点以下井段属于单相气流;②压井液发生下落,井底压力小于地层压力,连通点以下井段发展为稳定的零表观液速两相流;③压井液发生下落,连通点以下的井段被压井液灌满,井底压力大于地层压力,整个井筒为纯液流动。
3)通过提高压井液的切力,能够使连通点处快速满足临界携液气速条件,可以缩短压井成功时间,提高压井效率。
