基于隐马尔可夫模型的公交乘客出行链识别方法
2020-08-03崔洪军张晓阳朱敏清
崔洪军, 张晓阳, 朱敏清
(1.河北工业大学土木与交通学院,天津 300401; 2.河北工业大学建筑与艺术学院,天津 300401)
IC卡的广泛应用在各大城市中产生了海量的乘客出行信息数据,基于IC卡数据样本量大、信息储存量高、更新速度快、较手工收集数据方法更为准确且成本低廉等特点,可用其对乘客的出行特征、交通运营情况等进行描述及刻画。通过对IC卡和GPS数据进行识别分析可获得更为完整的公交乘客出行信息,同时对于公共系统的规划发展有着重要的意义。
目前在中国运营的公交车辆存在着两种计费方式:一票制上车打卡方式(如天津公交)及分段计价上下车均打卡方式(如北京公交);而一票制的计费方式在中国被大多城市所采用。一票制计费缺少乘客的下车站点具体信息,因而无法直接利用所得数据推算乘客出行信息。如何高效、准确地补全乘客的下车站点信息成了研究的热点及难点。国外对基于IC卡数据的乘客出行研究相对较早:Zhao[1]基于出行链思想,结合自动收费系统(AFC)、自动定位系统(AVL),实现了公交-地铁、地铁-地铁两种出行方式的下车站点的推导。Alex[2]基于出行链模型对公交乘客下车站点进行了判断,并生成了种子矩阵以实现对不同规模OD矩阵的预测。Farzin[3]基于巴西圣保罗的公交乘客出行数据,以总数据量的5%为数据样本,推算了乘客的下客站点。Barry等[4]提出经典出行链假说,并以此推断了纽约市公交乘客的下客站点。较之国外,中国对此方面的研究起步稍晚。胡郁葱等[5]通过数据挖掘技术获取公交OD矩阵。陈峥嵘[6]利用智能公交数据处理方法对公交客流OD进行研究。胡继华等[7]结合出行链模型对公交乘客的下车站点进行概率推算。吴祥国[8]提出可根据乘客多日出行链进行下车站点判断,但并未提出相应的算法,只能通过人工识别。
由以上研究成果可知,国外研究人员由于研究数据较为丰富、全面,故利用出行链方法得到的推算结果其准确性较高;中国因行政区划、数据兼容性等原因,可用于研究的数据通常不够完整。因此,完全搬用国外对于乘客完整出行信息的获取方法不切合实际。本研究将根据公交乘客IC卡信息对乘客出行目的进行识别,进而提取公交乘客的完整出行链。
1 乘客出行链提取
提取出行链,需对乘客的出行目的进行完善。翁剑成等[9]通过整合多源数据,提出了出行链提取的四阶段法,朱亚迪等[10]基于概率图模型对乘客的出行链进行了提取,并分析了乘客的出行特征。本研究基于广义出行链思想构建连续隐马尔可夫模型(CHMM),进而对乘客的出行链进行提取并分析其出行目的。
1.1 模型构建
隐马尔可夫模型由马尔可夫模型及高斯混合分布共同构成,用五个元素来描述,其中包括隐藏状态集合0、可观测状态集合、初始状态概率矩阵π、隐含状态转移概率矩阵A、观测状态转移概率矩阵B。其转化机理如图1所示。
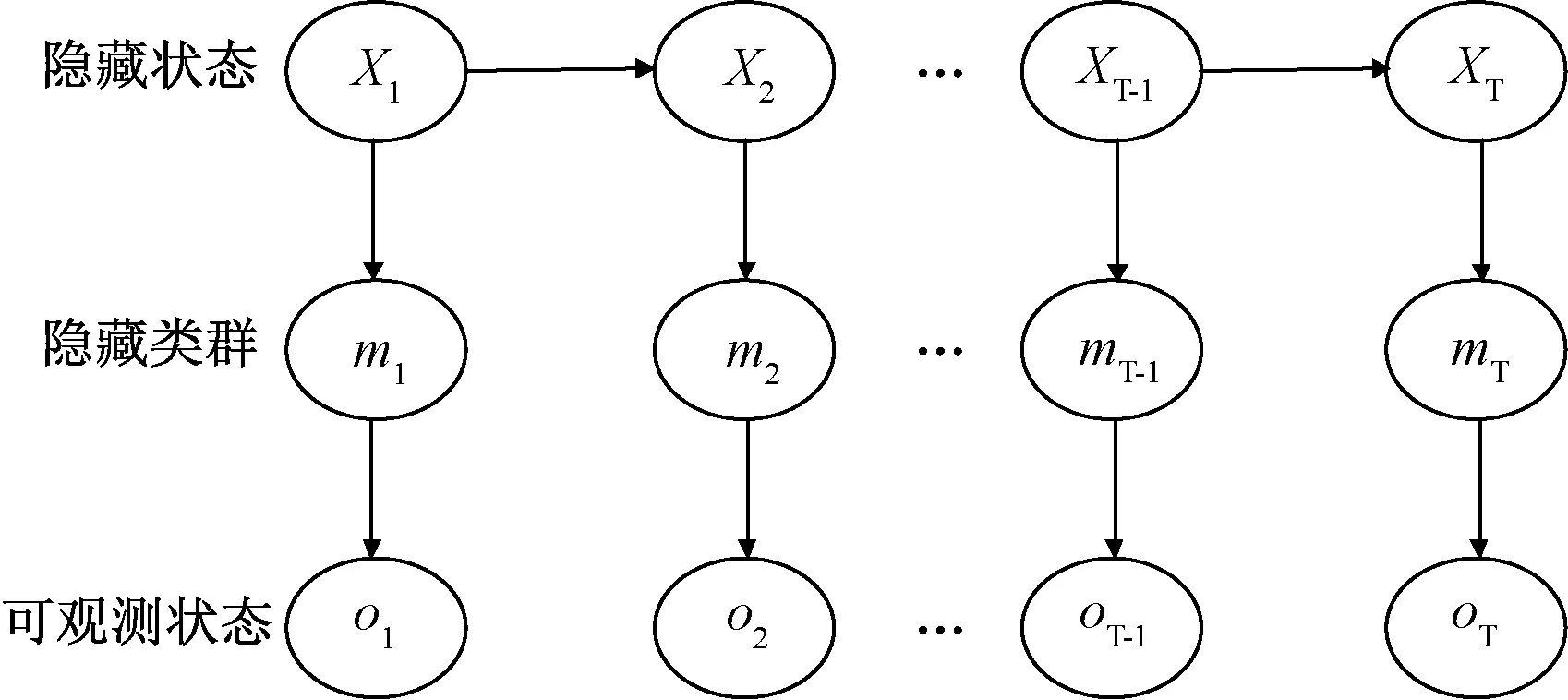
图1 连续隐马尔可夫链转化机理Fig.1 The mechanics of determining states and observations behind a CHMM
选定的出行活动序列在其初始状态时的概率集如式(1)所示:
π={πi}={P(xi=i)}, i=1,2,…,N
(1)
式(1)中:在初始状态下,xi为出行链活动序列的初始状态变量,为出行活动次数,i表示总数N中的第i个出行活动;πi为第i个出行活动在初始状态下的概率,π是初始概率的一个向量;两个连续马尔可夫过程间的转移概率矩阵如式(2)所示:
A={aij}={P(xt=j|xt-1=i)},
i,j=1,2,…,N
(2)
式(2)中:xt为出行链活动序列中的第t个状态,aij为在第t-1个状态下活动i变为第t个状态下活动j的转移概率。在出行链中,出行目的mt为隐藏状态,从隐藏状态变为可观察状态的输出概率为gxik。因可观察变量ot为连续变量,将其分成K类可观察状态。在此,假设状态k对应的可观察参数服从均值、方差分别为μk、σk的高斯分布,其分布矩阵见式(3):
G={gik}={P(mt=k|xt=i)}, i=1,2,…,N, k=1,2,…,K
(3)
对于活动序列中出行目的为i的第t个出行,其观察参数为ot的概率可由式(4)表示:
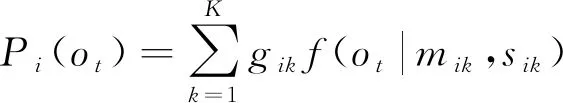
(4)
式(4)中:μik=μk,σik=σk,i=1,2,…,N,k=1,2,…,K,由以上向量集合组成的可观测状态参数集合由式(5)表示:

P(o1,o2,…,ot|[π,A,G,{μk},{σk}])=
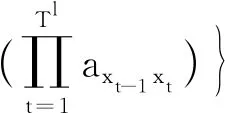
(5)
1.2 模型求解
采用前向后向算法可对可观测状态对应的出行链概率进行计算,在得到概率后,可采用Baum-Welch算法对隐马尔可夫模型进行参数估计,继而通过Viterbi算法根据参数估计结果完成出行链提取。具体推导过程参见参考文献[11]。
2 数据处理
2.1 数据结构
研究数据来源为石家庄市公交IC卡及公交GPS数据,其中IC卡基础数据为数据卡ID编号、刷卡时间、车辆号、车辆线路号等,GPS数据包括车辆终端号(车辆号)、GPS系统时间、经纬度数据、GPS接收时间等;同时IC卡基础数据中的车辆号对应GPS数据中的车辆终端号。只选取研究所需数据,数据结构如表1所示。
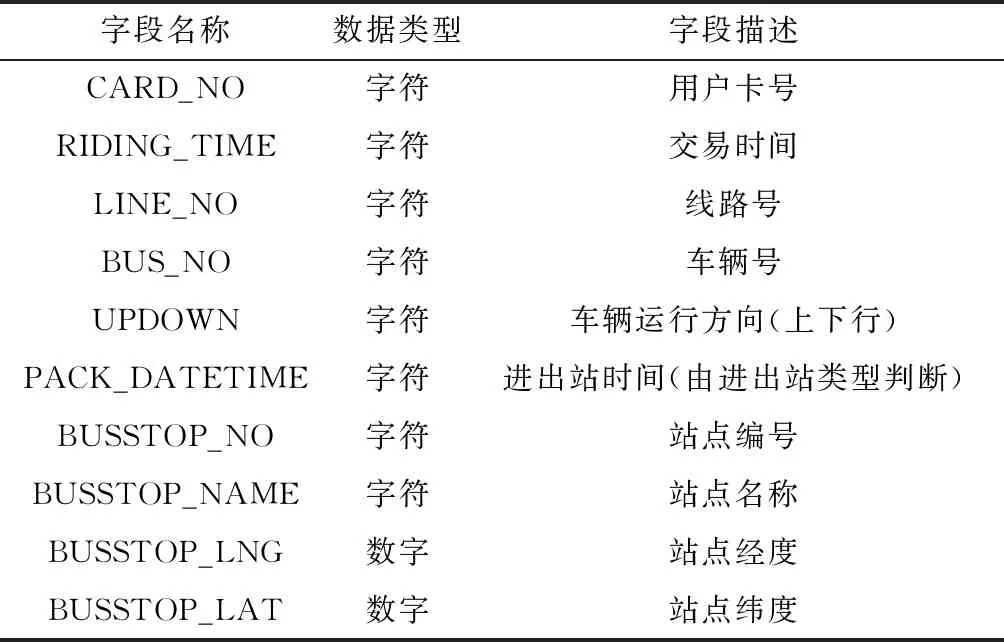
表1 研究数据描述
2.2 基于时间数据匹配的上车站点识别
对于上车站点的识别,中国学者有较多的研究[12-13]。利用基于时间数据匹配的识别方法:将IC卡刷卡数据中的交易时间与GPS系统中的进出站时间相比对,若打卡交易时间在车辆进出站的时间范围内,则认为该时刻车辆所处站点为乘客的上车站点。即对于任意刷卡记录,其交易时间tri与车辆的进出站时间taj、tdj满足
taj≤tri≤tdj
(6)
则在此进出站时间时车辆所对应的站点为乘客的上车站点。
3 模型验证与分析
3.1 模型验证
采用2018年某一周工作日石家庄智能公交卡数据对模型进行实现,并在同一时期同区域公交站点附近进行了居民出行调查,调查所得数据用以与模型识别结果进行对比分析。
按照前述模型,根据乘车时间,结合乘车站点周边土地利用情况进行算法优化,对可观测状态进行聚类,聚类结果如表2所示。可观测状态的六个状态类分别对应五个不同的活动类,分别为通勤(W)、外出办公(B)、购物(S)、回家(H)、其他(O),对应关系见表3。可以看出以通勤和回家为目的的出行活动具有很强的时效性,而其他类型的活动出行时间分布则较为广泛。
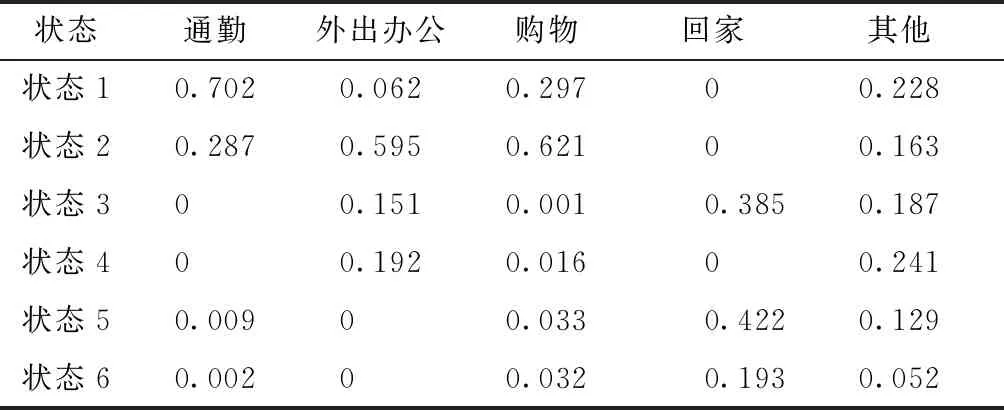
表3 可观测状态与出行目的对应结果
将模型识别结果对乘客出行目的进行统计,并与实际调查结果进行对比,对比情况见表4。

表4 模型识别结果与调查结果对比
根据对比结果,模型对以通勤和回家为目的的活动识别结果与调查结果吻合度较高,误差率分别为12%、6%,而对其他类型的活动识别结果则偏差略大,这也表明在石家庄公交车出行是居民较为主要的通勤方式,而在进行其他活动时人们往往更倾向于选择其他更为便捷交通方式,而这可能也是导致模型对其他类型出行活动识别结果不够准确的因素之一。
3.2 结果分析
根据模型识别结果,各活动之间的转移概率如表5所示。活动间的转移概率可在一定程度上反映居民出行链中活动与活动间的相互关系。可以看出,乘客通勤之后最可能的行程是回家;外出办公之后行程为回家的居多,返回工作地的次之;购物之后回家的可能性最高,而在基于家的活动之后通勤出行概率最大;在进行其他类型的活动之后往往会继续进行该类活动。各类型出行链占比如表6所示。由表6可知,通勤活动是公交出行链中最主要的部分。

表5 活动间转移概率
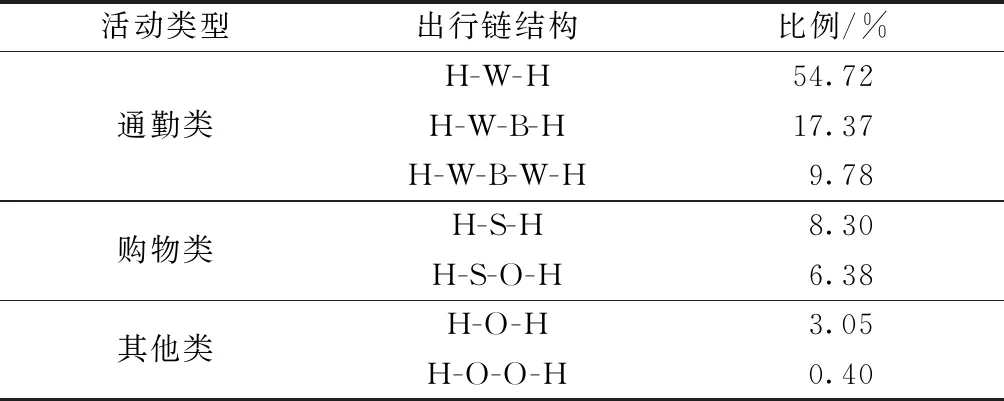
表6 各类出行链占比
4 结论
利用公交IC卡数据,基于乘客乘车时间及乘车站点周边土地类型,构造隐马尔可夫模型对其出行目的进行识别,进而提取公交车乘客出行链,从出行链角度对乘客出行特征进行研究。得出如下结论。
(1)利用乘客公交IC卡数据,结合站点周边土地类型构建隐马尔可夫模型,对乘客出行目的进行识别,进而提取完整出行链以研究出行特征。模型识别结果与实际调查结果相比吻合度较好。
(2)在工作日,公交车乘客以通勤为目的的出行最多,其他类型的活动选择公交以外的出行方式的可能性更大。
(3)公交车乘客的通勤出行具有很强的时效性,其他类型的活动出行时间分布则无固定时间。
