基于绿色通信的大规模多输入多输出天线选择算法
2020-08-03李作洲庞二强李新宇
李作洲, 庞二强, 李新宇
(大连海事大学信息科学技术学院,大连 116026)
多输入多输出(multiple-input multiple-output,MIMO)技术在发射端和接收端分别使用多个发射天线和接收天线,可以极大提高系统容量[1]。大规模MIMO技术是5G无线通信的关键技术。天线数量的增加,使得射频链路也随之增加,相应的功率也会增加,因此需要降低功率,提高系统能源效率,实现绿色通信。近年来提高MIMO系统的能源效率成为了研究热点[2]。
为了实现绿色通,在大规模MIMO系统中通常要进行天线选择[3],其中追求系统容量最大化是最基本的天线选择算法[4-9],该类算法中最优天线选择(optimal antenna selection, OAS)算法[4]采用了穷举法,然而在大规模MIMO系统中,这种算法开销很大,因此出现了次优天线选择算法。
文献[5]采用基于范数的天线选择(norm-based selection, NBS)算法,然而信道的范数是信道矩阵的某一行(列)的总体状况,不能精确地表示系统容量。因此这类算法在选择一根天线时,信道容量较高[6-7],而对信道矩阵的某些行(列)接近线性相关时,这种方法得到的系统容量明显下降。文献[8-9]提出了递增天线选择(incremental antenna selection, IAS)算法,算法依据信道状况进行容量计算。该方法考虑信道矩阵的每一个元素,对信道的分析更加准确;而且该方法可以选择出任意的天线子集,从而克服了NBS算法的缺点。虽然该类算法在天线选择时考虑了信道系数或信道矩阵,但均没有考虑天线发射功率,这可能会导致算法为了单纯追求容量最大而增大天线发射功率的结果,即天线数量减少的同时,可能会导致总的发射功率增加。
随着绿色通信的兴起,天线选择在追求容量最大化的同时,出现了各种以提高能源效率为目标的天线选择算法[10-13]。文献[10]提到随机天线选择算法(random antenna selection, RAS),该算法在基站天线数量远大于终端数量的情况下与最优选择性能相近,但该结论基于信噪比近似为常数,而这种情况只适用于基站天线数量大于小区用户数量10倍以上的情况。文献[11-13]提出了二分搜索算法(binary search algorithm, BSA)。该算法基于序列搜索算法,文中证明了在大规模多输入单输出(multiple-input single-output, MISO)系统中,随着系统天线数量增加,能源效率会先递增再递减,因此采用二分法进行天线选择。但这是在信道硬化下得到的,即在天线数量巨大时,信道参数会逐渐的趋于稳定。然而当考虑信道参数波动时,不同天线数目的能源效率并不是严格的先递增后递减,此时二分法可能会出现优化退化,导致局部最优。
大规模MIMO技术是5G通信中最重要的技术之一,绿色通信是5G移动的发展趋势,因此本文提出了基于博弈论的天线选择算法(antenna selection algorithm based on game theory, AS-GH)。在大规模MIMO系统下行链路中,通过系统容量、发射功率和能源效率的博弈实现全局最优。博弈论实现了多目标的折中,避免了因单纯追求系统容量最大化而导致能源效率的下降。
1 信道模型与信号模型
1.1 信道模型
国际上许多研究机构对MIMO信道进行了大量的数据测量和评估,并提出了不同的信道模型。其中欧盟的WINNER(wireless world initiative new radio)项目,广泛地研究了不同场景,提出了WINNER II信道模型[14],该信道模型得到了业界的广泛认可。WINNER II信道支持2~6 GHz载频,相对于3GPP(3rd generation partnership project)提出的SCM(spatial channel mode)信道模型,更能满足5G通信的需求。因此采用WINNER II信道模型,并且在原有模型上做了适当简化。
1.1.1 发射导向矢量和接收导向矢量
从基站到用户的视距方向包含了发射端信号的离开角度,接收端信号的到达角度,二者共同组成了信号的指向性,再结合天线结构就形成了信号导向矢量。
发射导向矢量表示为
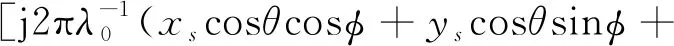
zssinθ)]
(1)
式(1)中:θ为发射导向矢量的俯仰角;φ为发射导向矢量的水平方位角;xs、ys和zs为第s个发射天线的位置矢量;λ0为信号的波长。
接收导向矢量表示为
(2)
式(2)中:ψ为接收导向矢量的俯仰角;φ为接收导向矢量的水平方位角;xu和yu为第u个接收天线的位置矢量。
1.1.2 信道模型
基站第s个发射天线到接收端第u个接收天线,第l条多径对应的信道系数为

(3)
〈rs,Φl〉=xscosθlcosφl+yscosθlsinφl+
zssinθl
(4)
〈ru,Ψl〉=xucosψlcosφl+yucosψlsinφl
(5)

假设有L条多径,则多径信号合成的信道系数为
(6)
假设系统中有N个发射天线,有K个用户,每个用户有M个接收天线,则第k个用户的信道传输矩阵为
(7)
1.2 信号模型

(8)
2 基于绿色通信的天线选择算法
大规模MIMO系统的天线选择,不仅需要考虑信道容量,还需要考虑能源效率,只有综合考虑上述因素的影响,才能取得最优的天线选择。基于此,本文采用了AS-GH算法,通过博弈论的纳什均衡选择发射天线。
2.1 基于博弈论的天线选择算法
通信系统的信道容量是系统传输最大数据率的表征。MIMO系统天线数量的多少可以直接影响系统信道容量。第k个用户对应的信道Hk的容量计算公式为
(9)
(10)
效用函数Uk由系统容量和发射功率组成,该函数最大值点,即纳什均衡点,体现了容量和发射功率的折中,由此可以确定天线数量和索引。该博弈过程的伪代码描述如下:

fork=1:1:K{
forn=1:1:N{
计算第k户,第n个天线的容量
fork=1:1:K{
forn=1:1:N{

计算n个天线对应的发射功率:
计算效用函数值:
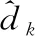
2.2 能源效率
由式(10)可知,在AS-GH算法中,效用函数为
即
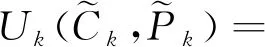
(11)
根据式(11),定义能源效率E为
(12)
能源效率是单位能量所支撑的系统容量。由式(11)和式(12)可以看出,效用函数(10)与能源效率函数式(12)是对数关系。因此效用函数式(10)和能效函数式(12)具有相同的变化趋势。效用函数式(12)的最大值点(均衡点)对应能源效率的最大值点。
2.3 基于博弈论的天线选择算法均衡点存在性证明
U=log2(1+C)-P
(13)
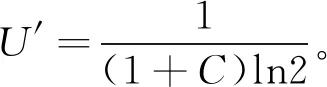
U′对C求导:
(14)
证毕。
3 仿真结果
3.1 发射天线功率、容量及能源效率的关系
表1以用户2为例给出发射天线功率、系统容量与能源效率关系的仿真。系统为4个发射天线,4个用户,每个用户4个天线,发射功率取归一化,取值范围在0~1之间。
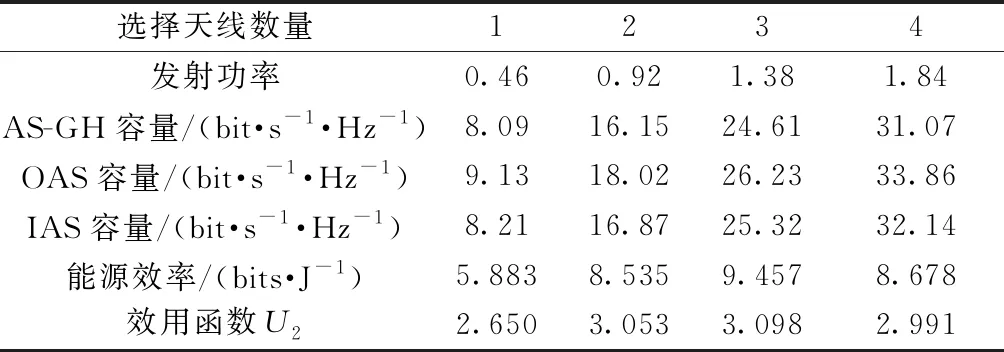
表1 发射天线功率、容量与能源效率的关系

由表1可以看出,AS-GH算法的容量接近OAS算法和IAS算法,在均衡点处,AS-GH算法的容量与IAS仅相差2.8%。这说明AS-GH算法在兼顾发射功率的同时,仍可保持较高的容量。
3.2 基于容量最大化的天线选择算法与基于博弈论天线选择算法的比较
本节的仿真是基于容量最大化的天线选择算法的能源效率与AS-GH算法能源效率的比较。系统采用12个发射天线,12个用户,每个用户12个天线,比较IAS算法、NBS算法与AS-GH算法的能源效率,图1给出的是用户2的情形。由图1可以看出,AS-GH算法的能源效率高于IAS算法的能源效率,而IAS算法的能源效率高于NBS算法的能源效率。在各个算法的最大值处,AS-GH算法的能源效率比IAS算法的能源效率高9.2%,比NBS算法能源效率高27.5%。导致NBS算法能源效率低下的原因是:信道的范数并不能精确的描述系统容量,并且当信道矩阵接近线性相关时,相对于其他算法,NBS算法容量低很多,这就导致NBS算法能源效率的低下。AS-GH算法的效用函数包含了系统容量和发射功率,而IAS算法仅在考虑信道矩阵的条件下,优化信道容量,而没有考虑发射功率,导致IAS算法虽然在系统容量上略高于AS-GH算法,但能源效率却低于AS-GH算法。

图1 基于容量最大化与基于博弈论算法的能源效率比较Fig.1 Comparison of energy efficiency between based on capacity maximization and based on game theory algorithm
3.3 基于能源效率最大化的天线选择算法比较
本节为基于能源效率最大化的不同天线选择算法的比较,系统为12个发射天线,每个用户有12个天线。图2是用户2在各种算法下的能源效率,图3是各算法中所有用户能源效率的比较。其中,全部天线算法[15](all antenna selection, AAS)是指基站端的所有天线始终工作,即不进行任何天线选择。OAS算法是采用穷举的方法,遍历发射天线所有可能的功率和发射天线的子集及其对应的容量,找出能源效率最大的组合。
由图2和图3可以看出AS-GH算法的能源效率比BSA的算法、RAS算法及AAS算法的能源效率高,比OAS的能源效率低。由图2可以看出,AS-GH算法选择的天线数量为8,与OAS算法选择的天线数量相同,而BSA算法和RAS算法选择的天线分别为7和6。在各个算法的最大值处,AS-GH算法比BSA算法高8.9%,比RAS算法高21.8%;并且在天线数量为8时,AS-GH算法比BSA算法能源效率高10.0%,比RAS算法能源效率高23.2%,而仅比OAS算法低4.3%。这说明AS-GH算法不仅可以选择出与OAS算法相同的天线数量,而且AS-GH算法的能源效率也最接近OAS算法,因此AS-GH算法更接近最优解。AS-GH算法比BSA算法能源效率高的原因是,BSA算法只有在发射天线和接收天线数量都很大时才能达到较高的能源效率,在不满足此条件时,能源效率并不会随着发射天线数量的增加而严格的呈现先增加后减小的趋势。这将导致最优解可能在折半查找中被舍去,使算法陷入局部最优,而AS-GH算法的能源效率是基于效用函数的纳什均衡得到的全局最优解。图3中AAS算法需要所有发射天线都工作,实际上没有进行天线选择,导致能源效率最低。RAS算法在基站天线数量大于终端数量10倍以上的情况下能源效率才比较高,因此RAS算法的能源效率仅略高于AAS算法的能源效率。

图2 能源效率与选择天线数量的关系Fig.2 Energy efficiency versus the number of selected antennas
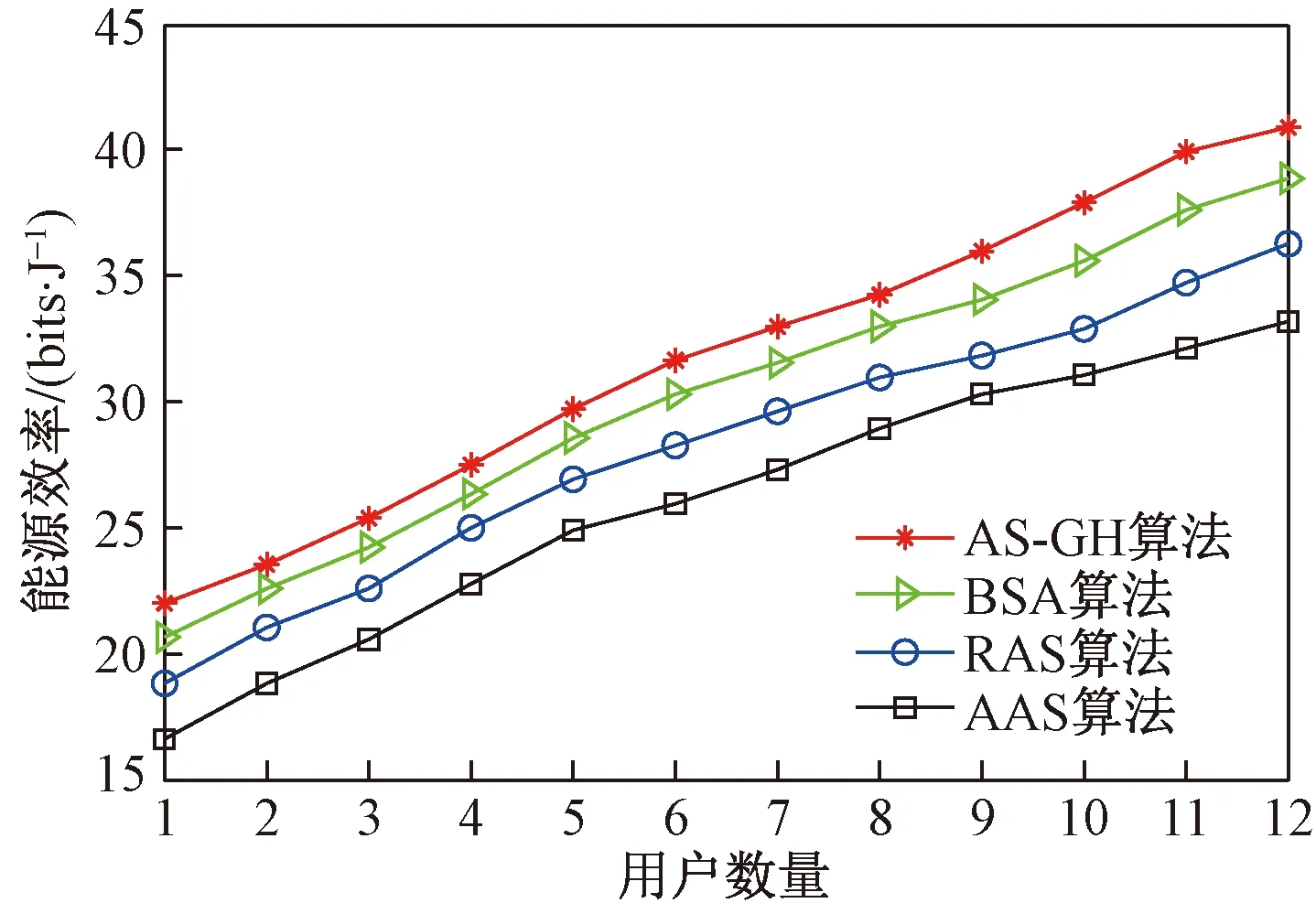
图3 能源效率与用户数量的关系Fig.3 Energy efficiency versus the number of users
3.4 AS-GH算法可靠性验证
表2和图4是基站为32个发射天线时的仿真,32个用户,仿真给出的是用户2的情形。此仿真的目的是验证仿真中基站天线数量与实际基站天线数量相近时AS-GH算法性能的可靠性。从图4和表2中可以看出,随着选择的发射天线增加,能源效率先增加再减小,在天线数量为18时,能源效率达到最大值点26.4 bits/J;并且从图4可以看出,在能源效率增加阶段,能源效率增加的幅度随着天线数量的增加而减小。导致上述现象的原因是在式(12)定义的能效函数中,分子是随着工作天线数量增加而近似于线性增加的系统容量,而分母是所有工作天线功率之和的指数函数。从仿真和理论分析可知,AS-GH算法的天线数量在接近实际基站天线数量时,仍然可以选择出使能源效率最高的天线数量,具有较高可靠性。

图4 AS-GH算法的可靠性验证Fig.4 Reliability verification of AS-GH algorithm

表2 AS-GH算法的可靠性验证
4 结论
在大规模MIMO系统中,由于大量的天线同时工作,引起功率的增大,因此系统必须进行天线选择。在天线选择时,通常要考虑系统容量,而在绿色通信中,能源效率也是一个重要的因素。本文利用系统容量和发射功率构造博弈论的效用函数,通过纳什均衡得到系统最优的发射天线。仿真结果表明,基于博弈论的天线选择算法与其他算法相比,具有更高的能源效率,即均衡的考虑发射功率和系统容量,不仅能提高能源效率,而且也符合绿色通信的发展趋势。
