充液格栅结构抗射弹冲击数值模拟研究

张 宇, 王彬文, 刘小川, 惠旭龙, 杨 欢

(中国飞机强度研究所结构冲击动力学航空科技重点实验室，西安 710065)

油箱结构是飞机和装甲车最容易受到威胁的关键部件。当射弹高速穿透充液箱体时，射弹通过与流体的阻尼作用将动能传递到箱体壁板，从而引起箱体结构灾难性的破坏。

在20世纪70—80年代，国外就已经开展贯穿弹道物冲击充液箱体结构研究。其中Fuhs等[1]、Patterson[2]、Bless等[3]、Lundstorm等[4-5]基于实验数据，发现射弹的质量和入射角度是影响冲击过程中射弹动能损失的主要因素。Varas等[6]基于试验研究了高速射弹冲击不完全充液铝管，发现充液比例越高，铝管产生的塑性变形区越大。为了提高箱体抗射弹冲击毁伤能力。Townsend等[7]通过引入低阻抗来干扰或分散射弹冲击产生的冲击波来减小箱体的毁伤破坏，但该方法引入更加复杂的结构，降低整体结构的可靠性。Disimile等[8]在箱体内部设计锯齿结构，通过波的相互作用破坏、抵消冲击过程中产生的冲击波，保证结构的安全性，并验证了该结构的有效性，但该设计只能降低特定方向射弹产生的破坏。Guerrero等[9]提出了铝蜂窝式方法，通过在铝管中填放铝蜂窝材料，限制空腔的扩展膨胀，减小射弹冲击对充液铝管的变形损伤。

实验研究虽然能直接观察到实验现象，获得所需的实验参数，但射弹高速冲击充液箱体实验研究费时费力，测试过程复杂。随着有限元方法的发展，采用数值模拟手段研究充液箱体抗射弹冲击性能已经成为研究该问题的主要途径和方法。目前针对射弹高速冲击充液箱体数值仿真，常用的方法有耦合欧拉-拉格朗日(coupled Euler-Lagrange，CEL)法、随机拉格朗日-欧拉(arbitrary Lagrangian-Eulerian，ALE)法、光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)法等。Sparks等[10]采用SPH方法和CEL方法研究射弹冲击充液箱体过程，发现SPH方法可以用更少的单元实现对冲击过程的模拟，但计算时间较长。Varas等[11-13]采用SPH和ALE两种方法建立有限元模型，研究冲击速度和充液比例对充液箱体抗冲击性能的影响，发现ALE方法中射弹速度误差更大，但在相同的网格密度下ALE方法得到的压力精度更高，此外冲击速度越大、充液比例越高，箱体毁伤程度越重。韩璐等[14]研究2枚射弹不同间距打击、2枚射弹不同时间间隔打击以及多枚射弹同时打击下充液箱体的毁伤效应，发现箱内液体的压力峰值来源于射弹入水后形成的冲击波，且多枚破片入射时液体压力有明显的叠加效应，箱体壁板的变形随射弹数量的增加显著增大。Liu等[15]研究箱体内部橡胶夹层对壁板的动态响应影响，发现其可有效缓解壁板的动态响应峰值，减小壁板变形；David等[16]研究了不同构型金属夹层壁板对充液箱体抗冲击能力的影响，发现夹层壁板构型对其抗冲击能力影响较大。

上述研究表明，中外学者针对充液箱体抗射弹冲击毁伤已经做了大量的工作，并得到了很多有用的结论。但目前学者们的工作集中于单个充液箱体，而飞机机翼整体油箱类似于长方体多胞充液箱体结构。因此，基于经验证的SPH-FEM动力学建模方法，建立充液格栅结构有限元模型，研究射弹初速度、充液比例、流体液面压力以及流体黏性等对冲击过程中射弹速度衰减变化规律、空腔形态变化规律以及流固耦合对格栅结构前、后壁板变形的影响。

1 数值模型

基于文献[17]经验证的SPH-FEM动力学建模方法，建立3×3典型充液格栅结构抗射弹冲击数值模型(图1)，计算时长2 ms。

图1 格栅结构有限元模型Fig.1 Finite element model of grid structure

格栅结构采用2024-T42铝合金材料，材料参数如表1所示。尺寸700 mm×700 mm×700 mm，外层壁板5 mm，内层壁板2 mm。射弹采用4340钢材，前段半球直径12.7 mm，后端柱体长度75 mm。

表1 2024-T42铝合金材料参数

格栅结构及射弹(参数见表2)采用Lagrange单元建模。考虑冲击过程中损伤区域集中在冲击点附近，为提高计算效率，将冲击点附近网格加密，设置为1 mm。最终格栅结构划分为94 206个单元，射弹划分为752个单元。

表2 射弹材料参数

流体采用SPH单元(参数见表3)建模。考虑内部壁板厚度对流体分布的影响，对不同格栅胞元内的流体单独建模，避免出现初始穿透。100%充液情况下流体划分为464 752个单元粒子。

表3 SPH单元材料参数

2 数值模拟结果与分析

射弹动能是充液格栅结构能量的唯一来源，因此可通过射弹动能变化表征充液格栅结构总能量变化；且格栅结构外壁板的变形是衡量充液格栅结构毁伤程度最直接因素。

因此以射弹初速度、充液比例、流体液面压力以及流体黏性等为变量，研究射弹冲击过程中射弹速度变化规律、空腔形态变化规律以及流固耦合作用下格栅结构前、后壁板的变形。

2.1 充液比例

为研究充液比例的影响，分别建立充液比例为70%、80%和100%三种充液格栅结构，保证射弹运动过程中完全浸入流体。射弹初速度为900 m/s。

数值模拟分析得到的射弹速度-时间曲线如图2所示。可看出，当射弹完全浸入流体时，不同充液比例下获得的射弹速度衰减变化规律基本一致，说明充液比例对射弹速度衰减变化规律基本没有影响。

图2 格栅结构射弹速度变化Fig.2 Variation of projectile velocity with grid structure

射弹冲击不同充液比例格栅结构形成的空腔形态如图3所示，并分别给出距离射弹尖端100 mm和210 mm处空腔尺寸直径。可看出，当射弹完全浸入流体时，形成的空腔近似为圆锥形；但空腔尺寸随充液比例的增大而减小。说明充液比例越大，空腔上方流体质量越大，导致流体和空腔接触界面上的压力越大，即表面张力变大，对空腔的形成有一定的抑制作用，导致空腔尺寸减小。其中100%充液格栅结构产生的空腔尺寸比70%和80%充液格栅结构形成的空腔尺寸分别小20.7%和24.4%。

图3 不同充液比例下格栅结构空腔形态变化Fig.3 Cavity morphology change of grid structure under different filling ratios

图4给出了前壁板和后壁板在射弹冲击时的变形情况。可看到，三种充液比例下后壁板变形最严重，70%、80%和100%充液比例下后壁板的变形比前壁板分别大27.1%、39.3%和41.1%；充液比例对格栅结构壁板的变形趋势影响较小；但格栅结构壁板变形量随着充液比例的增加而略微增大；且在冲击点以下[图4(a)横坐标<350 mm]前壁板变形对充液比例不敏感，在冲击点以上[图4(a)横坐标>350 mm]前壁板变形随充液比例增大而急剧增大。这是因为在冲击点以下充液比例对射弹传递给流体的能量影响较小，而冲击点以上射弹传递给流体的能量可通过流体向自由界面运动而释放，因此充液比例越小，前壁板变形程度越小。

图4 不同充液比例下格栅结构前、后壁板变形Fig.4 Deformation of front and rear panels of grille structures at different filling ratios

2.2 射弹速度

射弹初始动能是冲击过程中充液格栅结构获得的能量来源，决定了其毁伤程度。建立充液比例为80%的充液格栅结构，考虑射弹初始速度分别为600、750、900 m/s。

不同速度冲击下数值模拟得到的射弹速度-时间曲线如图5所示。可看出，射弹初始速度越大，速度衰减越快；但射弹初始速度越小，射弹穿透充液格栅结构的时间越长。表4给出了射弹的初始速度和对应剩余速度。发现射弹初始速度对动能损失比例影响较小，但初始速度越高动能损失绝对值越大。

图5 格栅结构射弹速度变化Fig.5 Variation of projectile velocity with grid structure

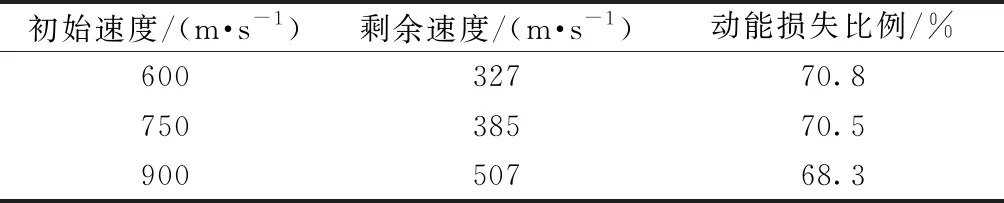
表4 射弹速度

不同初始速度下形成的空腔形态变化如图6所示，并分别给出距离射弹尖端100 mm和210 mm处空腔尺寸直径。可看出，随着射弹初始速度的增大，流体从射弹获得的动能和势能越多，因此形成的空腔尺寸逐渐增大。900 m/s冲击下形成的空腔尺寸比750、600 m/s冲击下形成的空腔尺寸分别大1.8%和4.5%。

图6 不同射弹速度下格栅结构空腔形态变化Fig.6 Cavity shape change of grid structure at different projectile velocities

图7给出了前壁板和后壁板的变形情况。可看到，后壁板变形最严重，600、750、900 m/s冲击速度下格栅结构后壁板变形比前壁板分别大64.8%、57.0%和39.3%，且格栅结构壁板变形程度随着射弹初始速度的增加而增大。说明初始速度越大，射弹通过黏性阻尼作用传递给流体的能量越多，增强流体与格栅结构壁板之间的流固耦合作用，导致壁板变形更加严重。

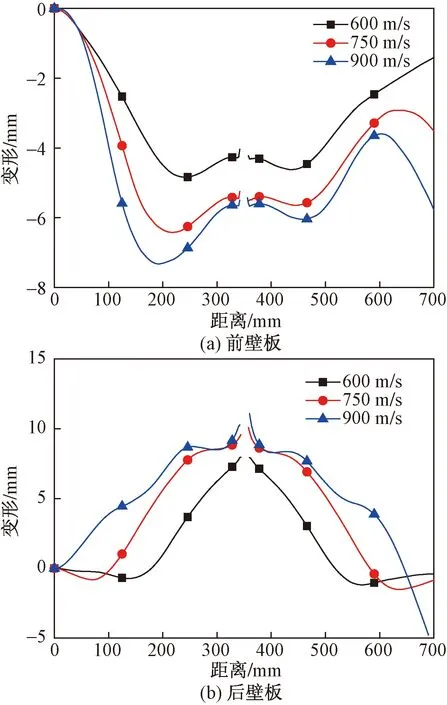
图7 不同射弹速度下格栅结构前、后壁板变形Fig.7 Deformation of front and rear panels of grille structures at different projectile velocities

2.3 液面压力

在飞机实际飞行中，为保证燃油供给，常常采用燃油箱增压方式。为研究液面压力的影响，分别设置液面压力为0.2、0.5、1 MPa，其中充液比例80%，射弹速度为900 m/s。

液面压力为0.2、0.5、1 MPa时射弹冲击过程中获得的速度-时间曲线如图8所示。可看出，随着液面压力的增大，射弹剩余速度逐渐减小。说明随着液面压力的增加，射弹与流体之间的阻力系数逐渐增大，导致射弹速度衰减更快。

图8 格栅结构射弹速度变化Fig.8 Variation of projectile velocity with grid structure

不同液面压力下形成的空腔形态变化如图9所示，并分别给出距离射弹尖端100 mm和210 mm处空腔尺寸直径。可看出，形成的空腔尺寸随着液面压力的增大而减小，液面压力1 MPa下产生的空腔尺寸比0.2和0.5 MPa液面压力下形成的空腔尺寸分别小8.1%和6.0%。说明随着液面压力增大，流体和空腔接触界面上的压力逐渐越大，对空腔的扩展有一定的抑制作用。

图9 不同液面压力下格栅结构空腔形态变化Fig.9 Cavity morphology change of grid structure under different liquid pressure

图10给出了射弹冲击下前、后壁板的变形情况。可看到，后壁板变形更加严重，0.2 MPa、0.5 MPa和1 MPa液面压力下后壁板变形比前壁板变形分别大40.9%、46.4%和39.3%；且液面压力越高，格栅结构前、后壁板的变形越大。说明液面压力越高，流体与格栅结构之间的流固耦合作用越强，进一步加大格栅结构的变形。

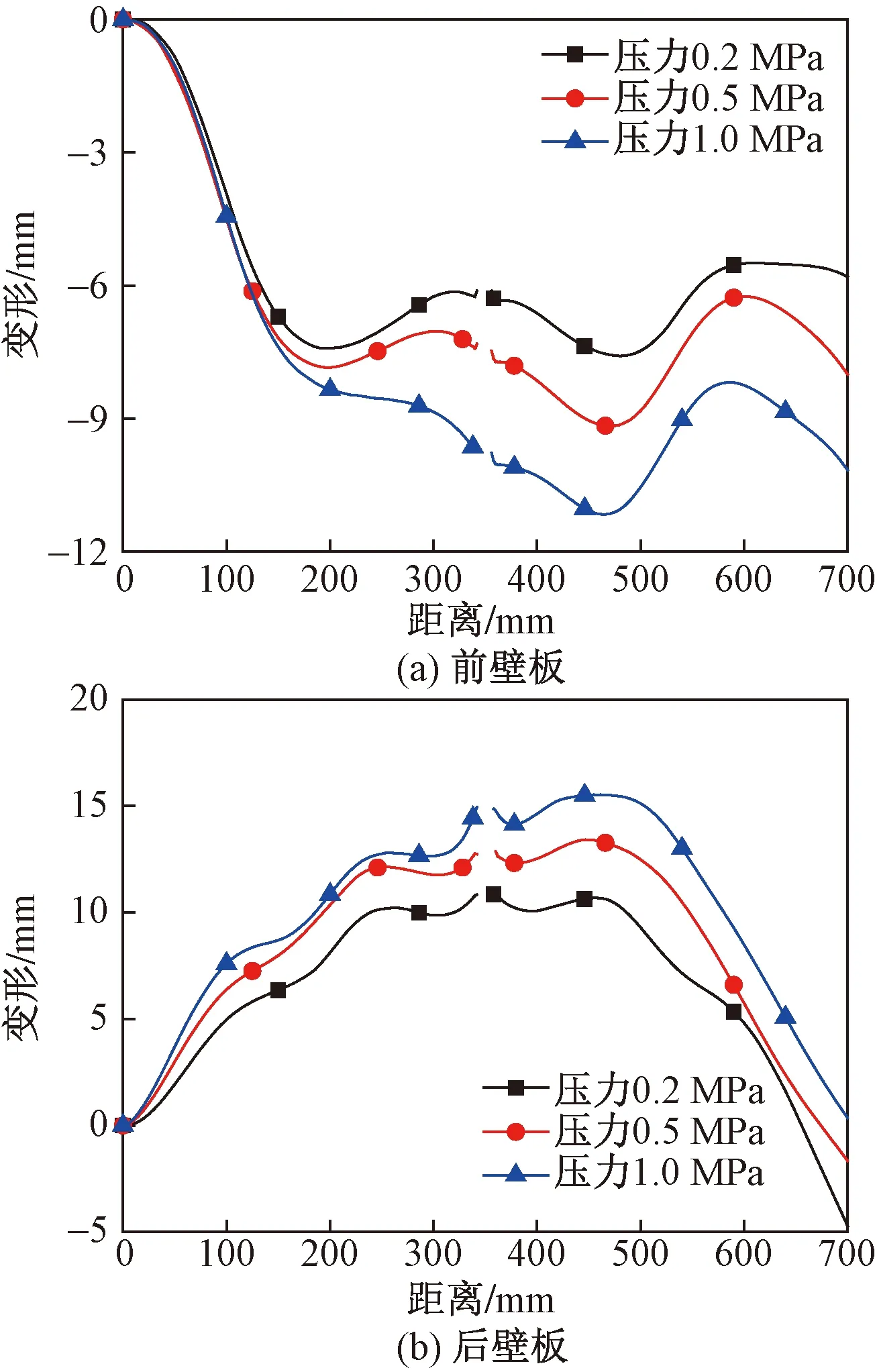
图10 不同液面压力下格栅结构前、后壁板变形Fig.10 Deformation of front and rear panels of grille structures under different liquid pressures

2.4 流体黏性

在飞机服役过程中，需要经历各种极端天气影响，外界温度以及航空煤油牌号对航空煤油的黏性均有较大的影响。因此通过修改*MAT_009-NULL中的黏性系数(见表5)，研究流体黏性的影响。其中充液比例为80%，射弹初始速度为900 m/s。

表5 不同工况下流体黏性数值

工况1、2和3下射弹冲击充液格栅结构过程中获得的速度-时间曲线如图11所示。可看出，随着流体黏性的增大，射弹剩余速度逐渐减小。这是由于随着流体黏性增大，流体和射弹之间的黏性阻尼作用加强，阻力系数增大，从而导致射弹速度衰减更快，剩余速度减小。

图11 格栅结构射弹速度变化Fig.11 Variation of projectile velocity with grid structure

图12不同流体黏性下形成的空腔形态变化，并分别给出距离射弹尖端100 mm和210 mm处空腔尺寸直径。可看出，流体黏性越大，形成的空腔尺寸越小，工况3产生的空腔尺寸比工况1、2产生的空腔尺寸分别小22.3%和2.6%。这是因为流体黏性影响流体和空腔接触界面上的表面张力，流体黏性越大，接触界面的表面张力越大，需要更大的压力载荷才能导致空腔进一步增大，从而对空腔的扩展有一定的约束作用，导致空腔尺寸越小。

图12 不同流体黏性下格栅结构空腔形态变化Fig.12 Cavity morphology change of grid structure under different fluid viscosities

图13给出了射弹冲击下前壁板和后壁板的变形情况。可看到，前壁板的变形与流体黏性无关，但后壁板变形随着流体黏性增加而略微增大。说明随着流体黏性增大，格栅结构后壁板损伤加重。

图13 不同流体黏性下格栅结构前、后壁板变形Fig.13 Deformation of front and rear panels of grid structures under different fluid viscosities

3 结论

基于经验证的充液箱体抗射弹冲击动力学建模方法，建立充液格栅结构抗射弹冲击动力学模型，研究射弹速度、充液比例、流体液面压力以及流体黏性等参数对充液格栅结构抗射弹冲击性能的影响。主要结论如下：

(1)射弹动能损失与充液比例基本没有关系，但液面压力和流体黏性与射弹动能损失正相关；随着射弹初速度增大，射弹动能损失绝对值增大，但动能损失比例变化较小。

(2)冲击过程中射弹动能转化为流体动能及势能，形成空腔结构；空腔结构的尺寸与射弹速度正相关，但与充液比例、液面压力以及流体黏性负相关。

(3)充液格栅结构壁板变形程度与充液比例、射弹速度和液面压力正相关，但与流体黏性基本没有关系，且后壁板的变形程度大于前壁板的变形；

(4)射弹冲击下，充液比例越高、射弹初始速度越高、液面压力越高、流体黏性越大，充液格栅结构越容易发生失效。