导流能力不均匀的部分压开垂直裂缝试井分析方法
2020-08-03王西强万奇锋程时清邸士莹
王西强, 万奇锋, 魏 婷, 冷 福, 魏 操, 程时清*, 邸士莹
(1.长庆油田分公司第七采油厂,西安 710200;2.中国石油大学油气资源与工程国家重点实验室,北京 102249)
水力压裂技术已经成为改造油气藏,提高单井产能的主流手段。为了合理评价压裂效果,必须准确分析油气井流入动态。Muskat[1]最早研究垂直裂缝井的压力不稳定特性和流体的流动方式;Prats[2]最先提出裂缝导流能力和井筒有效半径的概念,解决了不可压缩流体在高导流垂直裂缝中的渗流问题;Russell等[3]指出靠近无限导流裂缝区域为线性流,远离裂缝区域为径向流;Ramey等[4-5]引入瞬时Green函数和Newman乘积原理,同时提出将测压点选在无量纲裂缝长度的0.732处得到无限导流垂直裂缝井底压力解;Cinco等[6-7]提出半解析有限导流垂直裂缝模型,通过求解Fredholm型积分方程得到井底压力并划分了四个典型流动阶段;Cinco等[8]给出天然裂缝性油藏有限导流垂直裂缝半解析解,该种方式可避免对时间差分;Gonzalez等[9]考虑变导流系数和变表皮系数给出了实空间下垂直裂缝的半解析解;刘慈群等[10]利用椭圆流方程求解关于有限导流垂直裂缝的渗流问题;黄瑶等[11-12]考虑裂缝闭合和地层损害建立有限导流裂缝模型。但是没考虑压裂后铺砂不均匀和压裂液返排造成裂缝近井端导流能力强,尖端导流能力差和裂缝高度小于储层厚度的情况[13];另外,对于储层厚度较大的块状油藏,由于储层物性差异,导致在压裂时不可能将储层完全压开[14]和对于含底水的油井,常采用部分压开来防止底水锥进[15]。Kuchuk等[16]利用Green函数法给出了垂向各向异性部分射开井的压力分布表达式;卢德唐等[17-18]用Green函数法分别对部分压开油井和气井的井底压力进行了计算。综上,针对水力压裂后支撑剂难以到达裂缝尖端的问题,基于裂缝导流能力非均匀,并考虑不能完全压开储层的情况,建立垂向各向异性储层中导流能力不均匀的部分压开垂直裂缝试井模型。
1 部分压开两段导流系数垂直裂缝模型
1.1 物理模型
如图1所示,均质无限大储层中存在一口部分压开直井。裂缝以井筒为中心对称,方向平行于x轴,半长为xf,宽度为wf,高度为hf 图1 部分压开两段导流系数垂直裂缝物理模型Fig.1 Physical model of a partially penetrated well with a two-segment vertical fracture 基本假设:①油藏顶底封闭,水平方向无限大;②油藏为垂向各向异性,即水平方向渗透率kx=ky=kh,垂向渗透率kz=kv;③裂缝部分压开地层,即裂缝高度小于地层厚度(hf 裂缝内流量不均匀分布,缝内导流能力也不同,沿裂缝存在压力降,故模型的建立分为两部分。首先建立裂缝流动模型;然后建立油藏流动模型,将压裂裂缝看成线源,通过对点源函数积分得到无限大油藏垂直裂缝井的压力分布式;最后将油藏模型和裂缝流动模型耦合得到部分压开两段导流系数垂直裂缝的井底压力解。 1.2.1 裂缝流动模型 对于裂缝而言,可看作在y方向有源项qf(单位裂缝长度流量)流入裂缝;同时考虑到填砂裂缝体积相对较小,忽略弹性的影响[6],则有: (1) (2) (3) 式(1)~式(3)进行Laplace变换并求解得: (4) 1.2.2 油藏模型 根据高春光[15]对各向异性油藏渗流理论的研究,垂向各向异性部分打开储层压力分布式为 (5) 式(5)中:考虑裂缝中流量为均匀分布。将压裂裂缝看作线源,对式(5)进行积分得到线源任意一点(xD,yD)的压力分布。考虑无量纲线流量qfD(xD,yD)沿裂缝为非均匀分布,无法从积分中提出。最终得到垂向各向异性部分打开储层中压裂直井的井底压力分布式。 (6) 1.2.3 半解析井底压力解 在裂缝壁面处基质与裂缝压力相等,即 (7) 用边界元法将裂缝离散为N个等长小段(如图2所示),每个离散段内流量是均匀的。联立上述模型得到: 图2 i和j位置示意图Fig.2 The locations of i and j (8) (9) (10) (11) 当存在井筒储集CD和表皮S时,可以利用Hurst等[20]给出的表达式: (12) 上述公式中的无量纲量定义如下: 将无量纲裂缝半长离散为N=20段[22],近井端(前10段)无量纲导流系数FcD1=200,尖端(后10段)无量纲导流系数FcD2=10,hfD=0.2,得到垂向各向异性储层中部分压开两段导流系数垂直裂缝井的试井典型图版,如图3所示。根据压力及压力导数曲线特征,可划分7个典型阶段以及过渡阶段:①井筒储集阶段:压力和压力导数表现为斜率为1的直线;②过渡阶段:该段持续时间由井筒储集系数和表皮系数大小决定;③线性流阶段:包括双线性流阶段和线性流阶段,由于井储和表皮效应的影响,图3(a)仅能明显地看到线性流阶段,压力及压力导数曲线表现为斜率为0.5的直线,可通过图3(b)(不考虑井储表皮)观察双线性流特征;④两段导流特征段:压力导数曲线为斜率介于0.25和0.5的直线;⑤早期径向流阶段:在压力导数曲线上表现为斜率为0的水平直线;⑥球形流阶段:为部分压开地层的流动特征,在压力导数曲线上表现为斜率为-0.5直线;⑦系统径向流段:在压力导数曲线上表现为数值为0.5的水平直线。 图3 部分压开两段导流系数裂缝典型图版Fig.3 Type curves of partially penetrated well with two-segment conductivity fracture 垂向各向异性储层部分压开两段导流系数垂直裂缝模型中考虑因素较多,未知变量较多。本文针对主要因素,对各向异性程度、地层压开程度、裂缝导流能力和裂缝有效铺砂长度进行敏感分析。 将无量纲裂缝半长离散为N=20段,近井端(前10段)无量纲导流系数FcD1=200,尖端(后10段)无量纲导流系数FcD2=100,在图4中给出了各基础参数的值,得到了考虑各向异性程度的典型曲线。对于上下边界封闭的垂向各向异性部分压开储层,各向异性程度影响球形流及早期径向流的出现及持续时间。各向异性程度越大,球形流及早期径向流出现时间越晚;随着垂向各向异性程度下降,球形流的持续时间减少,早期径向流的持续时间增加。当kh/kv=1时,球形流的持续时间短,典型特征几乎消失了,而早期径向流的特征特别明显,在无量纲导数曲线上呈现双“台阶”的特征,这是由于裂缝的高度特别小,出现了类似水平井的垂向径向流阶段,在试井解释时这种情况将对井的类型判断产生干扰。 图4 不同各向异性程度对压力及压力导数曲线的影响Fig.4 Effect of different anisotropy degree on pressure and pressure derivative curves 基本参数设定同上,kh/kv=10,设置不同的hfD得到不同地层压开程度的试井典型曲线如图5所示。地层的压开程度主要影响线性流和球形流阶段。地层的压开程度越小,出现球形流的时间越早,球形流持续时间越长;随着压开程度增大,地层线性流的持续时间增加,而球形流持续时间缩短;地层的压开程度不会影响系统径向流阶段。 此外,储层不同压开程度下虽然试井曲线的形状相似,但压力和压力导数的值差别却很大(表1):同一时刻(如tD=10-5),完全压开储层的无量纲压降大约为hfD=0.8时的2倍;hfD=0.5时的3倍,无量纲压力导数大约为hfD=0.8时的2倍;hfD=0.5时的4倍。而在试井解释时通常认为地层完全压开,这势必会对解释结果的准确性产生极大的影响。 水力压裂后,支撑剂难以到达裂缝尖端,裂缝将会出现不同位置导流能力不同的情况,本文用两段导流系数来定量表征裂缝的导流能力,将无量纲裂缝半长离散为N=20段,近井端(前10段)无量纲导流系数为:FcD1=200,尖端(后10段)无量纲导流系数FcD2分别为100、10、5、1,得到试井分析的典型曲线(如图6所示)。裂缝尖端的导流系数下降会对井底压力响应产生很大影响。尖端导流系数越小,线性流段越明显,持续时间越长,而两段导流系数特征段的持续时间不断减少。 图6 不同裂缝导流系数对压力及压力导数曲线的影响Fig.6 Effect of different fracture conductivity on pressure and pressure derivative curves 将无量纲裂缝半长离散为N=20段,近井端无量纲导流系数为:FcD1=200,尖端无量纲导流系数为:FcD2=10,在图7中有计算所需的基础参数。考虑有效铺砂的裂缝长度对应的离散段N1分别为0、5、10、15、20,得到典型曲线(如图7所示)。压裂裂缝的有效铺砂长度主要影响双线性流段、两段导流特征段的出现时间及持续时间。有效铺砂长度越大,双线性流段的持续时间越短,两段导流特征段的出现时间越早,持续时间越短,线性流段的出现时间越早,持续时间越长。 图7 不同裂缝有效铺砂长度对压力及压力导数曲线的影响Fig.7 Effect of different values of effective sanding length on pressure and pressure derivative curves 新疆油田一口压裂直井新井投产日产油37.27 m3·d-1,压恢测试时间95.98 h。由于井储和表皮影响,两段导流系数特征段被掩盖,但根据压裂施工报告知地层未完全压开,通过解释该井来验证本文提出方法的实用性。基础参数如下:井径0.07 m,储层有效厚度15 m,有效孔隙度0.158,综合压缩系数0.001 9 MPa-1,地层原油体积系数1.175,地层原油黏度5.84 mPa·s,末点压力7.837 MPa。用本文提出的模型和Saphir软件有限导流模型解释上述压裂直井的实测数据如表2、图8所示。可以看出:如果忽略地层的压开程度和裂缝内不均匀分布的导流系数,解释得到裂缝半长和地层压力偏大,有效渗透率偏低。 表2 解释结果对比表 图8 实测数据与理论模型拟合图Fig.8 Fitting graph of theorical model and recorded pressure (1)裂缝内导流能力有差异会影响井底压力响应,压力的差异程度取决于裂缝两端导流系数比,在试井解释时应考虑这种情况对井底压力响应特征的影响。 (2)考虑裂缝内为两段导流系数,试井典型曲线会出现两段导流系数特征段:斜率介于0.25~0.5的直线段,这为识别压裂裂缝内导流能力不均匀提供了理论依据。 (3)对于上下边界封闭的垂向各向异性部分压开储层,各向异性程度和地层的压开程度会影响球形流及早期径向流的出现时间和持续时间。 (4)新疆油田某区块压裂直井实例解释表明,如果忽略地层的压开程度和裂缝内不均匀分布的导流系数,解释得到裂缝半长和地层压力偏大,有效渗透率偏低,新模型更加贴合实际情况。
1.2 部分压开两段导流系数垂直裂缝井底压力解











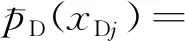




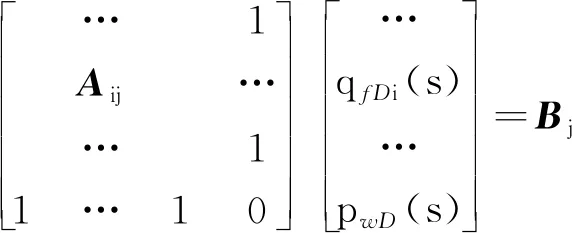
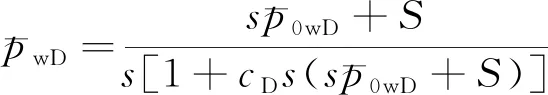
2 典型图版和流动阶段

3 敏感性分析
3.1 各向异性程度

3.2 地层压开程度
3.3 裂缝导流能力

3.4 裂缝有效铺砂长度

4 实例应用


5 结论
