智轨电车自动循迹感知与控制系统

袁希文，冯江华，胡云卿，张新锐，黄瑞鹏，林 军，袁 浩

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

智轨电车车体宽度为2.65 m，若要其在3.5 m宽的车道内正常行驶，特别是在狭窄区域转弯以及靠站停车，则需考虑占用道路宽度问题，以防止刮擦护栏或其他车辆现象的发生[1]。如果采用人工驾驶方式，不仅控制精度偏低，而且更容易因误操作[2]（90%以上的交通事故是由于驾驶员疏忽而导致的）而导致车辆偏离车道，继而引起交通事故。因此，设计一种自动控制系统来实现列车头轴精确跟随车道线行驶（即自动循迹），具有重要的现实意义[3]。智轨电车为3节编组、6轴全轮转向结构，自动循迹技术仅研究其头轴的路径跟踪控制问题；虽然第二轴至第六轴跟随头轴轨迹行驶的控制对智轨电车的正常运行也至关重要（决定了其跟随性和稳定性），但其功能由多轴液压转向控制系统实现，因此本文不作详细论述。

学者们对自动循迹的理论进行了大量的研究探索[4-6]，如基于车辆动力学模型的线性二次调节法（linear quadratic regulator，LQR）和模型预测控制(model predictive control, MPC)方法，以及基于车辆几何关系的Pure Pursuit方法和Stanley方法等。智轨电车是非线性、大延时的复杂系统，因此，在普通车辆基础上，需要特别考虑循迹过程中的感知延迟和控制延迟处理问题。文献[7-8]针对视觉延时对车辆转向控制的影响进行了研究，指出通过增大前视距离方法可以补偿相位延时。文献[9]利用频域和时域方法研究了视觉延时对控制系统性能的影响，并给出一个具有大时滞的视觉系统的设计实例。文献[10]在仿真中考虑了从图像采集到控制执行过程中的延时，所给出的延时参数为8 ms。文献[11]提出了一种基于视觉传感器的非均匀时延自动驾驶车辆的分级横向控制方法。上述文献虽然关注了视觉感知延时的影响，但均未考虑执行器的延时影响问题。

本文对智轨电车自动循迹系统进行了研究，介绍了该系统的组成，并阐述了基于深度学习的车道线识别与数字虚拟轨道生成算法；提出了2种考虑执行器延时的循迹控制方法，即基于视觉感知的PID控制方法和MPC方法；最后通过仿真和实车试验对这两种方法的循迹效果进行了验证。

1 自动循迹系统组成

自动循迹系统是一种通过在列车上增加图像识别传感器以提取车道线特征并进行分类、跟踪，再经反馈控制来实时调节车辆航向、跟踪期望路径的闭环系统[1]。图1示出智轨电车自动循迹系统构成，其包括感知子系统、控制子系统以及执行子系统。本文仅讨论感知子系统和控制子系统。

图1 智轨电车自动循迹系统构成Fig.1 Structure of the automatic tracking system for autonomousrail rapid tram

1.1 感知子系统

传统的循迹导航技术一般借助于无线通信来获取GPS全局定位信息，其对通信质量和可靠性要求极高；而逐渐成熟的图像感知技术不仅无需依赖于无线通信，而且适应性强、成本低，更适用于作为城市公共交通解决方案的智轨电车的定位。

智轨电车的感知子系统采用极简图像感知技术，突破了信息分离、标识、特征提取和连续数字轨道生成等难题，实现了在路面信息残缺、车辆随机振动条件下可稳定识别并形成数字轨道的功能。图2示出运行路径实时感知工作原理。

图2 运行路径实时感知原理Fig.2 Real-time perception principle of digital orbits

1.2 控制子系统

控制子系统根据感知子系统实时感知的车辆与虚拟数字轨道的距离偏差、角度偏差和道路曲率等信息并结合车辆状态参数，在中央控制计算单元进行实时计算，得到方向盘转角指令，然后将指令输入至转向执行子系统以调整车辆航向，使系统能够在列车架构特殊、初始姿态随机的情况下保证头轴自主、精确地进入和跟踪数字轨道。图3示出自动循迹控制原理。

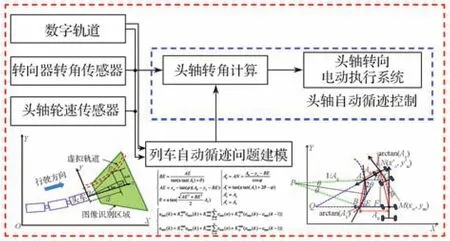
图3 自动循迹控制原理Fig.3 Control principle of automatic tracking system

2 车道线识别与数字虚拟轨道生成

传统车道线视觉识别算法是基于特征和模型检测机制，需根据不同场景调整检测算法，因此鲁棒性和泛化能力较差，处理的结果缺乏复杂多变环境的语义描述能力[12-14]。基于深度学习的车道线识别算法以最具代表性的深度卷积神经网络（FCN）为内核，利用卷积与池化操作提取图像的低层特征，将多种简单特征组合成更加抽象的复杂特征，并基于此实现目标功能，因此其在实践中具有良好的泛化学习能力，为复杂交通场景检测难题的解决提供了新思路[15]。本文采用深度卷积网络技术实现智轨电车专用车道线识别和数字虚拟轨道生成的功能。

2.1 基于深度学习的车道线语义分割算法

图像的语义分割算法旨在复杂场景下按照图像隐含的语义进行图像分割，是计算机视觉的核心任务之一，本文采用FCN作为语义分割的基础网络来提取智轨列车前视图像中的专用车道线。FCN在图像语义分割任务中使用卷积-反卷积操作来实现端到端的图像像素分类预测（图4）。其首先对图像进行卷积处理，提取图像的高维度特征图；然后使用反卷积操作，在高维特征图的基础上重建出与原图像分辨率一致的语义分割图像。

图4 FCN的编码-解码结构Fig.4 Encoding-decoding architecture of FCN

图像卷积操作的对象是前一层特征图中对应区域。前一层产生的特征图通过卷积核的卷积之后产生一个或多个特征图（图5），卷积流程符合式（1）要求。

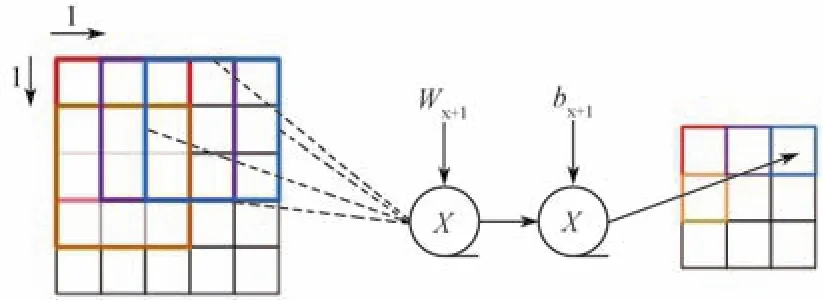
图5 神经元卷积流程Fig.5 Schematic diagram of convolution

相比于传统深度神经网络，FCN主要进行了全连接层卷积化、上采样、卷积与跳级结构等方面的优化；利用反卷积和跳跃支路，算法可以实现多尺度融合，并将特征图调整到指定大小。FCN损失函数是网络最后一层每个像素的分类损失函数之和，像素分类损失函数采用交叉熵，具体如式（2）所示。

式中：yi——标注真值；——预测值。

根据融合特征图的数量，FCN可派生出FCN-32s,FCN-16s及FCN-8s等多种不同预测精度的结构。FCN主干结构中的5个卷积层生成5种尺度的特征图，特征图从第一级到第五级尺度依次减小，而特征抽象程度依次增加。不同尺度的特征图融合时，依次从第五级向前添加，如图6所示。FCN-32s结构仅对pool5池化层输出的特征图进行操作，将尺寸为原图像1/32大小的特征图进行32倍反卷积输出，得到较为粗糙的预测结果。FCN-16s结构综合利用了pool4池化层和pool5池化层输出的特征图，先将第五级特征图进行2倍反卷积生成的特征图与第四级特征图叠加后，再进行16倍反卷积输出；相比FCN-32s输出，精度提高了一倍。FCN-8s进一步结合pool3池化层、pool4池化层和pool5池化层输出的特征图进行特征图叠加，再经8倍反卷积输出，精度比FCN-16s的提升了一倍。

图6 FCN跳跃结构Fig.6 Skipping Net of FCN

本文采用精度最高的FCN-8s结构来实现专用车道线的精准分割。FCN网络的训练需要采集涵盖多种天气光线条件下的智轨电车前视图像数据，以保证算法的泛化性能。智轨电车前视图像经过筛选与整理，去除了不符合条件的图像数据，对剩余的图像数据进行手工标定，制作成虚拟轨道识别训练集。使用训练集对深度卷积神经网络进行训练，得到用于识别车道线的FCN网络模型。在推理阶段，将FCN网络模型转化成TensorRT模型，进行FP16精度量化，以实现基于车载平台的实时推断部署。

2.2 数字虚拟轨道生成算法

车道线分割图像进行俯视变换后，受噪点和分割误差的影响，分割出的车道线不能准确地表征真实车道线的实际位置。为此，本文提取出车道线分割图像俯视图中的车道线坐标点，基于最小二乘法对车道线点集进行3次曲线拟合，然后再基于得到的3次曲线数字虚拟轨道方程来计算路径偏差。

图7描述了列车与专用车道线中心线的几何关系和摄像头视野图像平面。通过图像处理、特征提取及曲线拟合等方法，可得到基于车辆局部坐标系xoy的数字虚拟轨道，其计算方程为

式中：x——车辆纵向位置，向前为正；y——车辆横向位置，向左为正；A0~A3——曲线拟合系数，它们具有完备的物理意义，其中A0表示当前车辆第一轴中心与数字虚拟轨道的距离偏差，A1表示当前车辆航向与数字虚拟轨道切线方向的偏差斜率，A2表示曲率，A3表示曲率的变化率。

图7示出车-路几何关系和视野图像平面示意。其中，ld为车辆前视预瞄距离；φh(t)为车辆初始航向与虚拟轨道中心线切线方向的夹角，本研究中假设φh(t)为较小值；l为预瞄距离；y(l)为列车在l处的距离偏差，其包含yv(l)和yc(l)两部分，前者由前轮转角和车辆距车道线的侧向距离偏差引起，后者由道路曲率变化引起，见式（4）。

3 带延时的循迹控制方法

头轴方向盘输入与车轴输出之间一般存在200 ~500 ms的延时。在高速情况下，如果不考虑延时的影响，可能会导致车辆存在较大的横向偏差，甚至蛇形摆动或失去控制。由于减小或消除车辆机械硬件方面的延时普遍存在困难，因此本文采用考虑时间延时、动态预测的PID控制方法，通过预测车辆在延时后的位置和航向，使得循迹控制既能保证列车停靠站的精准性，又可保证高速行驶时的稳定性。图8示出系统控制原理。

一般而言，PID控制用于计算相对于当前状态的误差，但控制指令在车辆未来的状态执行；如果根据未来的误差计算当前控制指令，就必须引入车辆模型。因此，文中也介绍了一种显式地考虑时延的MPC控制方法，即利用车辆模型从当前状态预测延时后的车辆状态并以此作为MPC新的当前状态。

3.1 车辆运动学模型

智轨电车采用简化的自行车运动学模型作为其运动学模型，且不考虑轮胎因受力而引起的侧偏[16]，见图9。其中，lF和lR分别为车辆重心至前轴、后轴的距离；V为车速；β为车辆质心侧偏角；ψ为车辆航向角；R为质心处转弯半径；δF为前轮转向角；δR为后轮转向角，其作为输入参数，由多轴液压转向控制系统计算得出。

图9 车辆运动学模型Fig.9 Vehicle kinematics model

如图9所示，在固定坐标系XO’Y下，根据正弦定理，由ΔOCA得

再结合航向角公式：

3.2 延时预测模型

执行器的动态特性是导致延时的一个重要因素。例如，从给方向盘发送期望指令到车轮产生实际转向角之间的时间间隔，其可较易被建模并被纳入到车辆模型中。图10示出延时预测模型，其假定车辆在延时时间内恒速移动且车轮角度不变，M(0, 0)为车辆当前位置，N(xn,yn)为其延时T时间后的预测位置。

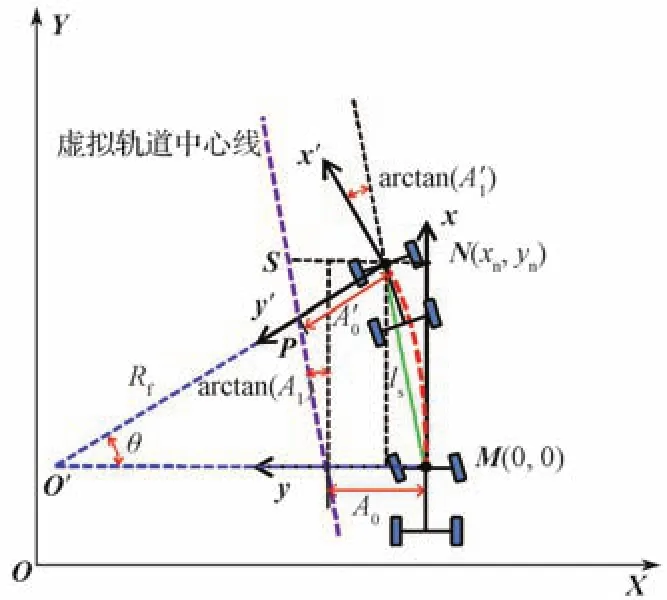
图10 延时预测模型Fig.10 Time delay prediction model

经过延时T时间后，车辆运动的位移为

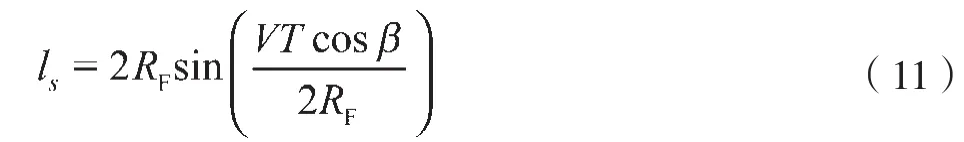
式中：RF——前轴中心转弯半径，且。

根据图10中ΔMO′N的几何关系：

由此获得相对于点M的点N的坐标为N(xn,yn)（即相对于车辆当前位置延时T时间后的坐标）：

在车辆局部坐标系xMy下，M(0, 0)点车道线方程系数分别为A0，A1，A2和A3；延时T时间后，N(xn,yn)点相应的车道线方程系数变为A0′，A1′，A2和A3。

一般情况下，执行系统延时时间对高速行驶车辆影响较大，对低速行驶车辆的影响较小，且车辆高速行驶往往是在直线或大半径转弯的路径上。因此，假设在延时时间T内，仅仅横向偏差和斜率发生变化，而曲率和曲率变化率的变化量均为0。根据图10所示，结合式（8），得到延时T时间后A1′的计算公式：

3.3 预瞄PID控制算法

驾驶员驾驶智轨电车时，通常目视前方一定距离的某个位置（即预瞄位置）实时调整方向盘操纵车辆。“预瞄”即模拟这种驾驶行为，通过图像识别方法获取前方某一距离处与轨道中心线的距离偏差、航向角偏差等信息，从而进行头轴期望转向角的计算。

根据延时T时间后预测位置的车道线方程系数A0′，A1′，A2和A3，得到预瞄距离l处的距离偏差ecte(k)和角度偏差eha(k)：

预瞄距离可以自适应速度的变化，其取值与速度相关，本文以车辆第一轴中心为原点，沿着车辆轴线方向的直线距离为预瞄距离（图7）。如果跟踪路径曲率较大，预瞄距离可采用弧长距离ld计算。

对距离偏差和角度偏差分别进行PID反馈控制，得到

式中：ucte(k)为预瞄点处距离偏差PID控制的控制量；uha(k)为预瞄点处角度偏差PID控制的控制量；KP,cte，KI,cte和KD,cte分别为距离偏差PID控制的比例、积分和微分系数；KP,ha，KI,ha和KD,ha分别为角度偏差PID控制的比例、积分和微分系数。

最终得到前轮转向角的控制量为

3.4 MPC控制

首先采用式（8）所示的车辆运动学模型作为预测模型。控制系统的输入变量和状态变量分别用u(δF)和χ(X,Y,ψ)表示，且其通用形式可表达为

对于参考轨迹，使用下标“r”表示参考量，将其形式转换为

将式（19） 在参考轨迹点采用泰勒级数进行展开，并用式（20）减去展开的式（19），可以得到车辆线性误差模型；再通过离散化，得到

延时预测处理：在每个时间步长t的基础上，通过延迟预测，得到新的t时刻的状态：

以上控制器状态变量是基于世界参考系，但是视觉循迹控制必须基于车身与车道线的相对位置偏差，因此需要将参考路径世界坐标点转换到以车辆为中心的参考系中。

为了确保智轨电车快速平稳地跟随虚拟轨道，在目标函数中考虑了状态偏差和控制增量的优化目标函数，具体如下：

其中：Q和G为权重矩阵；Np为预测时间域；Nc为控制时间域；为转换后的ctet和eψt状态变量；为控制变量的约束，反映了跟随目标轨迹的能力，=0。

经过一系列转换后，可以获得系统预测输出的表达式：

将式（24）代入式（23），转化目标函数为最优问题的标准二次型，并结合约束条件，求解二次规划问题[17]。

在解决每个控制周期后，可以获得有关时域的一系列控制输入增量：

在车辆转向系统上执行以上控制序列中的第一个元素，见式（26）；在随后的控制循环中重复该过程。

4 仿真分析与实车验证

4.1 仿真分析

在Trucksim软件中建立智轨电车动力学模型，在Matlab/Simulink中建立控制模型，通过联合仿真（图11），验证本文所提控制方法的有效性。仿真时，车速被设置为15 km/h。表1示出智轨电车动力学模型中基本尺寸参数。

图11 Trucksim与Matlab/Siumlink联合仿真模型Fig.11 Joint simulation model with Trucksim and Matlab/Siumlink

表1 基本尺寸参数Tab.1 Basic dimension parameters

利用正弦曲线仿真工况来验证PID控制方法的有效性（图12），可以看出，所设计的控制器可以较好地跟踪虚拟轨道。

图12 自动循迹PID控制仿真效果Fig.12 Simulation results of automatic tracking PID control

利用圆周曲线仿真工况来验证3 m/s和5 m/s 车速下MPC控制方法的有效性（图13）。可以看出，所设计的控制器可以稳定地追踪到虚拟轨道。

图13 自动循迹MPC控制仿真效果Fig.13 Simulation results of automatic tracking MPC control

4.2 实车验证

对自动循迹PID控制策略进行低速进站和高速行驶稳定性实车验证试验。

4.2.1 车道线识别测试

首先通过实车静态测量车道线识别误差，结果显示其识别精度在±5 cm内；然后分别实车动态测试白天和夜间的车道线识别效果，如图14所示。可以看出，识别的结果与真实车道线吻合得较好，且追踪稳定。

图14 车道线识别效果Fig.14 Testing results of lane line identi fi cation

4.2.2 精准停站测试

精准停站测试时，在进站前50 m处车辆被降速至15 km/h并保持；待进入站区后，继续减速，到停止线时，车速降为0。精准停站测试结果（图15和图16）显示，头车与站台间隙保持在10 cm左右，较好地满足了乘客上下车的舒适性需求；但由于列车车身较长且进站时车身铰接处存在微小的角度，使得前后间隙并不完全一致。

图16 精准停站离站台间隙测量数据Fig.16 Measurement data of clearance between precise docking and off-site

4.2.3 高速循迹测试

高速循迹测试时分别采用考虑延时和未考虑延时的控制方法，将列车由静止状态直线提速到50 km/h并保持一定时间，然后减速停车。图17示出这两种控制方法下自动循迹时列车横向偏差的对比。可以看出，在同等车速条件下，采用考虑延时的控制方法时，列车横向偏差较小且保持稳定；而采用未考虑延时的控制方法时，列车会蛇形摆动。

图17 两种控制方法自动循迹时列车横向偏差对比Fig.17 Two automatic steering control methods comparison in lateral deviation

5 结语

本文详细介绍了智轨电车自动循迹感知子系统和控制子系统，提出了一种基于深度学习的专用车道线识别与数字虚拟轨道生成方法，通过实车动态测试白天和夜间的识别效果，结果显示与真实车道线吻合得较好。此外，文中还分别提出了考虑智轨电车非线性、大延时特点的PID控制和MPC控制方法，仿真结果证实其跟踪数字轨道效果较好。最后，对所提出的PID控制方法进行了实车验证，结果表明：在同样车速条件下，本文所提出的方法使得列车在精准停站时，头车离站台间隙控制在10 cm内，高速循迹时横向偏差保持在±15 cm内，控制效果较好。

下一步将对MPC控制方法进行实车验证，测试其低速和高速的控制效果。未来还将进一步深入研究虚拟道岔、自动循迹停车入库等技术。