基于遗传模拟退火算法的自动化制造单元周期调度
2020-08-03唐秋华毛永年
王 娟,唐秋华,毛永年,3
(1.湖南工程学院机械工程学院,湖南 湘潭,411104;2.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;3.遵义师范学院工学院,贵州 遵义,563006)
随着企业自动化和智能化程度的提高,物料搬运工作越来越多地由机器人完成。机器人搬运作业顺序不仅影响其自身的工作效率,而且影响整个自动化制造单元的生产效率及生产计划的执行效果。在制定搬运机器人周期作业顺序时,若只有一台搬运机器人,只有一种工件进入或者离开系统,且工件的加工时间仅能在给定的上、下限范围内变动,则称之为具有作业时间窗约束的单机器人单度自动化制造单元调度问题。
针对这类问题,Phillips等[1]首次建立了混合整数线性规划模型,并构建了一个基准案例P&U。此后,研究者逐步提出了各种精确算法、启发式算法、元启发式算法来求解该问题。随着制造单元中工作站数量的增加,分支定界等精确算法[2-4]在求解速度上难以令人满意;而在使用启发式或元启发式算法时,首先面临的难题是所研究问题的可行解空间狭窄,难以找到可行解,更难接近最优解。为此,人们采取多种措施,如减小搜索空间、不可行解修复等,以加快求解速度。其中,晏鹏宇等[5-6]计算出最大在制品数量,据此将解空间分割成若干子空间,将搜索过程限定在子空间内,通过无效空间的剔除提高了算法收敛速度。王跃岗等[7]在混合量子进化算法中加入基于图论的不可行解修复策略。Lei等[8]在混合量子进化算法中加入启发式修复策略。毛永年等[9]在改进遗传算法中加入不可行解的判断方法和联动修复机制。然而,随着工作站数量增多和可行解比例变小,问题的求解难度变得更大,需要采取更加准确而有效的措施去发掘可行解空间,进一步提升求解速度和质量。
为此,本文提出一种具有修复机制的遗传模拟退火算法(简称“IGASA”)。该方法以遗传算法为基本框架,引入模拟退火机制,通过温降控制,从算法运行初期到末期递减较劣解的接受概率,实现全局搜索和集中探测之间的动态平衡,并对种群中的不可行解进行有限次的修复,从而提升可行解和最优解的甄别概率。
1 问题描述和数学模型
具有作业时间窗约束的单机器人单度自动化制造单元如图1所示,有一个装载站(编号为0)、n个工作站(编号为1~n)、一个卸载站(编号为n+1)和一个物料搬运机器人,加工一类相同的工件。每个工件从装载站进入制造单元中,顺次经过工作站1到n后,从卸载站离开制造单元。在装载站、各工作站和卸载站之间无缓冲区,工件在任一个工作站完成加工后(加工时间要满足时间窗约束),由搬运机器人搬运到下一个工作站。假设装载站与卸载站的容量无限大,每个工作站上最多只有一个工件在加工,机器人每次最多只能搬运一个工件。
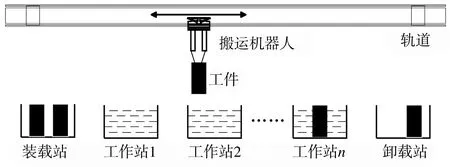
图1 自动化制造单元示意图
自动化制造单元的工作效率取决于对搬运机器人作业的合理规划。搬运机器人以一定的周期进行循环作业。在它的一个搬运循环周期内,只有一个工件投入生产,且只有一个工件出产。机器人的搬运循环周期时间即为相邻两个工件的出产时间间隔,被称为生产节拍或周期长度。对自动化制造单元进行周期调度,就是要找到最佳的机器人搬运顺序,从而使周期长度最短、生产率最高。为了减少周期长度,应尽量使各工作站能够并行作业,多个在制品同时进行加工,即在保证可行的前提下,跨周期的工序数尽量多。
图2为一个含有4个工作站的自动化制造单元的周期调度甘特图。若用搬运作业i表示机器人从工作站i上取下工件、搬运到工作站i+1并把工件装载到工作站i+1上的全部操作,则在图2中,机器人按照(0,2,4,1,3)的顺序循环作业。在一个周期T内,有3个在制品同时加工。工序1和3在一个周期内完成,而工序2和4则跨越了两个周期。
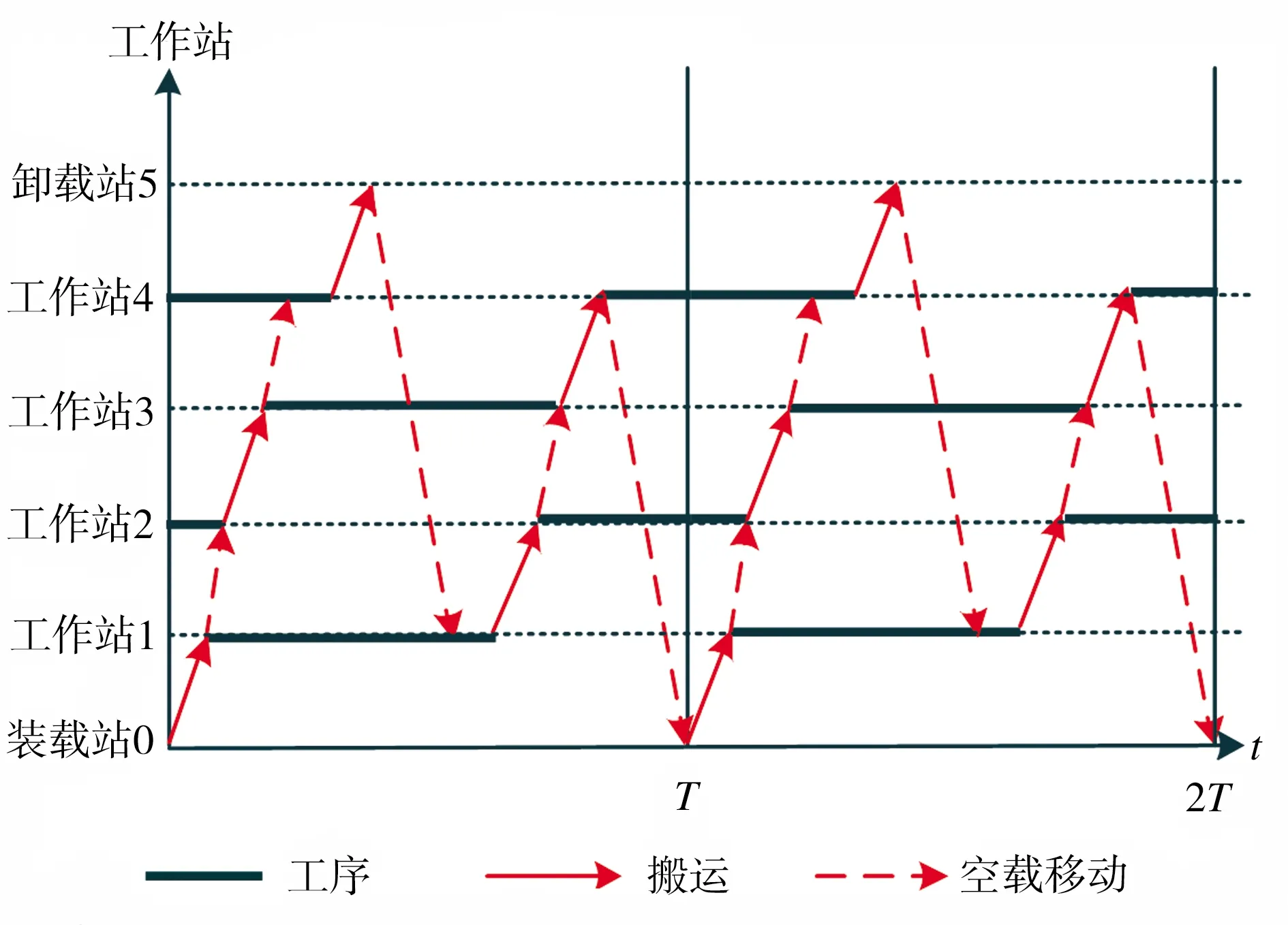
图2 含4个工作站的自动化制造单元周期调度Fig.2 A cyclic schedule for robotic cell with four workstations
为便于数学模型的表述,定义如表1所示的参数和变量。

表1 模型中的参数与变量
该问题的混合整数规划模型可以表示为:
minT
(1)
s.t.:
Qi+yi-1,i=1, 1≤i≤n
(2)
M(1-Qi)+bi≥ci,0+d0+c1,i, 2≤i≤n
(3)
yi,j+yj,i=1,i≠j,0≤i,j≤n
(4)
si-(sj+dj)+Myi,j≥cj+1,i,i≠j,1≤i,j≤n
(5)
si-(si-1+di-1)+M(1-yi-1,i)≥ai, 1≤i≤n
(6)
si-(si-1+di-1)-M(1-yi-1,i)≤bi, 1≤i≤n
(7)
(si+T)-(si-1+di-1)+Myi-1,i≥ai, 1≤i≤n
(8)
(si+T)-(si-1+di-1)-Myi-1,i≤bi, 1≤i≤n
(9)
T≥si+di+ci+1,0, 1≤i≤n
(10)
s0=0,Q0=1,Q1=0
(11)
si≥0, 1≤i≤n
(12)
模型的目标函数是最小化周期长度T。式(2)表示:若工序i跨越两个周期,则在一个周期内搬运i先于搬运i-1;若工序i在一个周期内完成,则在一个周期内搬运i后于搬运i-1。式(3)表示先后次序约束,当工序i满足bi 求解具有作业时间窗的单机器人单度自动化制造单元调度问题,就是要找出最佳的机器人搬运顺序,从而使周期长度最短。所以,在用改进遗传模拟退火算法进行求解时,解空间即为所有的机器人搬运序列组合,每个解(即染色体)用M=(m0,m1,…,ml,…,mn)表示,其中ml为一个周期内的第l次搬运作业的编号。机器人按固定的搬运顺序循环作业,任意一个非搬运作业0开始的解都能等价变换为以搬运作业0开始的解。以含有5项搬运作业的此类问题为例,解(0, 1, 2, 3, 4)与解(3, 4, 0, 1, 2)等价。为了保证解的多样性,采用以任意搬运作业为首的编码方式,随机生成Psize个循环序列,构成初始种群。 根据该问题的目标函数和跨周期决策变量Qi的特性,本文采用双适应度对解的质量进行评价。 第一个适应度参照文献[9]中的方法计算。对于任意给定的一个解,使用式(13)计算第一个适应度值: f1=T+ω3 (13) 式中:f1为第一个适应度值;T为解的最短周期长度;ω为解中不可行子序列的个数。 在计算适应度值f1之前,先对解进行可行性判别,同时得到ω值,判别方法参照文献[9]。若解可行,T可用文献[10]中的多项式算法求解。若解不可行,T可用式(14)表示: (14) 由于不可行解很多,且适应度f1相同的不可行解数量也较多,为了区分f1相同的不可行解的优劣,引入第二个适应度f2。f2表示解中跨周期工序数,其计算公式为式(15): (15) 对于可行解来说,周期长度越小,则跨周期工序数越多;反之则跨周期工序数越少。对于适应度f1相同的不可行解,跨周期工序数越多,可认为解更优,经过交叉、变异、修复之后更有可能变为跨周期工序数较多、周期长度较小的可行解。 在进化过程中,采用遗传算法中的选择、交叉、变异生成新解,同时分别在交叉和变异之后采用模拟退火算法中的Metropolis准则来判断是否接受新解,从而在保留优良的基因片段的同时,还能保持解的多样性。 (1)基于双适应度的选择操作 在进行选择操作时,采用锦标赛法从随机选择的两个染色体中挑选出较好的进入子代种群,步骤如下: 步骤1从种群中随机选择两个染色体(每个染色体入选概率相同) 。 步骤2若两个染色体适应度值f1不相等,选择f1较小的染色体进入子代种群;若两个染色体f1值相等,选择适应度值f2较大的染色体进入子代种群。 步骤3重复执行Psize次步骤1和步骤2,得到新一代种群。 (2)基于双适应度的交叉操作 在进行交叉操作时,顺次将子代种群中的染色体两两进行两点交叉。然后,对于种群中的每个染色体,使用Metropolis准则来判断是否接受新解,接受概率如式(16)所示。 (16) (3)基于双适应度的变异操作 在进行变异操作时,对于每个染色体,随机选择两个基因交换其位置。然后,对于种群中的每个染色体,使用Metropolis准则来判断是否接受新解,接受概率如式(16)所示。 具有作业时间窗的单机器人单度自动化制造单元调度问题的可行解非常少,对不可行解进行修复是提高搜索到可行解概率的非常有力的操作。种群初始化和更新之后,都需要对种群中的不可行解进行修复。在修复之前,先将其等价转换为以搬运作业0为首的序列,用M′表示,对M′进行两次修复。 (1)基于跨周期决策的先后次序约束修复 如果M′不能满足先后次序约束(见式(3)),则解不可行,采用下面的步骤进行修复: 步骤1找出满足bi 步骤2分析R中的任意一个搬运Rj在M′中的位置是否位于搬运Rj-1之后,若不满足,则将搬运Rj在M′中的位置调至搬运Rj-1之后。修复后的解用M″表示。 (2)联动修复 经过上述修复后得到的解M″不一定是可行解,对其进行可行性判断,若解M″可行,则可不进行联动修复,若解M″不可行,则需要进行联动修复,联动修复采用文献[9]中相应的方法。 根据经典的模拟退火算法和遗传算法的流程以及上述修复机制,给出IGASA算法的具体步骤: 步骤1设置初始温度T0(充分大)、终止温度Te、温度衰减率Pt、最大内循环次数Iloop、种群规模Psize、交叉概率Pc、变异概率Pm、最大迭代次数g、最大修复循环次数h;初始化模拟退火当前温度t←T0、内循环迭代计数器n1←0、迭代计数器n2←0。 步骤2随机生成初始种群。 步骤3判断种群中解的可行性,对可行解进行局部邻域搜索,对不可行解进行先后次序约束修复和联动修复。 步骤4对当前种群中的解进行评价,如果有比全局最优解更好的解,则保存该解为全局最优解,n2←0;否则,运用精英保留策略,将当前种群中最差的解用当前全局最优解替换,n2←n2+1。 步骤5进行选择操作。 步骤6进行交叉操作,应用Metropolis准则判断是否接受劣解。 步骤7进行变异操作,应用Metropolis准则判断是否接受劣解。 步骤8若n2 步骤9n1←n1+1。若n1 步骤10若t 表2 随机案例的测试结果 从表2中可以看出,随着不能跨周期工序数的增多,IGASAFR算法求解的精度总体上越来越高,单纯使用先后次序约束修复就可以得到最优解,而且,IGASAFR算法的速度比IGASASR算法快很多,即先后次序约束修复的速度远快于联动修复的速度。同时,随着不能跨周期工序数的增多,IGASA算法速度与IGASASR算法相比由略慢变化到略快,具体原因是:如果解中没有不可行子序列,则无需进行联动修复;在IGASA算法中,当不能跨周期工序数较多时,先后次序约束修复的作用比较大,经过此修复后,解中没有不可行子序列而能跳过联动修复的概率显著增加,从而使IGASA算法的求解速度比单纯使用联动修复的IGASASR算法要快。 为验证IGASA算法的性能,用该算法求解8个基准案例各10次,得到每个基准案例周期长度的最小值和平均值与最优解的百分率偏差,并与传统的遗传算法(GA)和模拟退火算法(SA)、HIGA算法[9]进行对比,所得实验结果如表3所示。单纯使用GA或SA时,8个基准案例中只有3~4个案例可以找到最优解。从表3可以看出,IGASA算法与HIGA算法有几乎相同的求解精度,但是前者的速度比后者快很多,基本上可以节约2/3的CPU运行时间。 表3 基准案例的测试结果 图3为用IGASA和HIGA求解基准案例Zinc的收敛曲线。从图3也可以看出,IGASA算法能以更快的速度搜索并收敛到最优解。IGASA算法能在更短的时间内求得基准案例的最优解或近优解,其原因在于:①遗传算法采用种群进行进化,可在整个解空间同时搜索,但具有较差的局部搜索能力;模拟退火算法的局部搜索能力虽然较强,但是采用单个个体进行进化,收敛速度慢;将两者结合,使全局和局部搜索能力都得到强化,可避免过早收敛。②采用双适应度对解进行评价,对于周期时间相同的不可行解,选择跨周期工序数大的解作为较好解,使其逐渐逼近最优解。③对不可行解进行两步修复,第一步保证不能跨周期的工序对应的两个搬运满足先后次序约束,第二步使用联动修复机制尽量使机器人移动能力满足工件的加工时间窗约束,使解以最大可能性朝着目标函数优化的方向进行调整。因此IGASA算法在搜索时既能保证解的多样性,又能使解朝着有用的、可行的方向进化,最终找到最优解。 图3 IGASA和HIGA求解案例Zinc的收敛曲线Fig.3 Convergence curves of benchmark problem Zinc by IGASA and HIGA 本文针对具有作业时间窗的单机器人单度自动化制造单元调度问题,提出了一种改进遗传模拟退火算法。在种群的进化过程中,利用选择、交叉、变异操作对解进行更新,并利用Metropolis准则判断是否接受交叉和变异后产生的劣解,使解保持多样性且避免局部最优。在选择操作和Metropolis准则中使用周期时间和跨周期工序数双适应度评价解的优劣,加大逼近最优解的概率。然后运用先后次序约束修复和联动修复机制对不可行解进行修复,避免算法的盲目搜索,提高搜索效率。通过对现有文献中基准案例的测试以及随机案例的测试,验证了该算法求解此类自动化制造单元调度问题的有效性和优越性。2 IGASA算法设计
2.1 编码方式和种群初始化
2.2 双适应度
2.3 解的更新
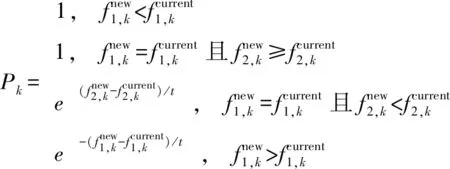
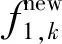
2.4 不可行解的修复
2.5 IGASA算法的步骤
3 实验验证
3.1 先后次序约束修复的效果分析

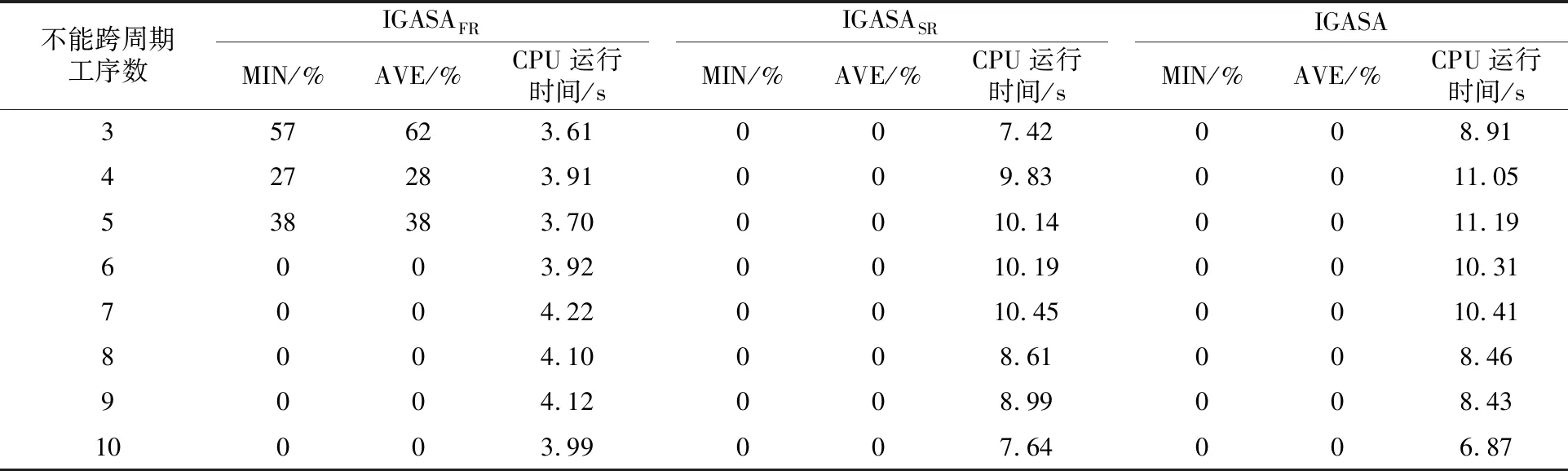
3.2 与其他算法的对比分析
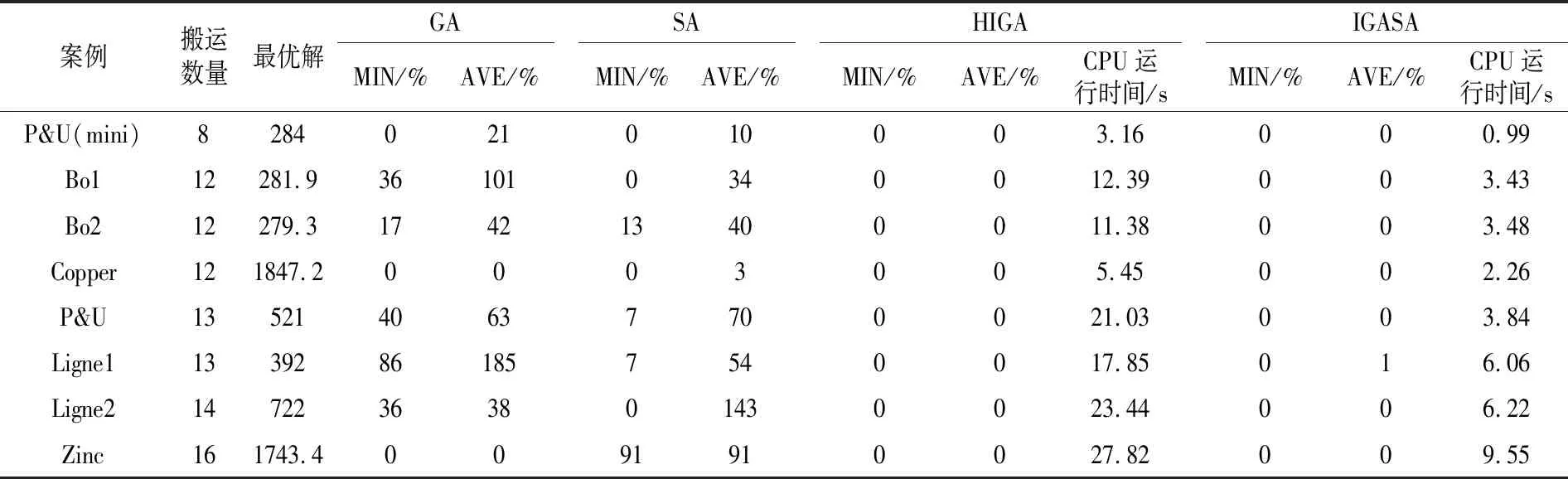
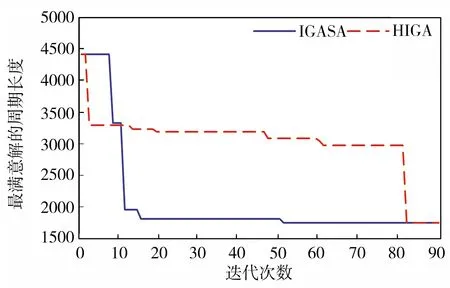
4 结语
