连铸机故障时融合炉次重分配的炼钢-连铸生产重调度

赵 阳，唐秋华，韩大勇

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081；3.武汉科技大学生产系统工程研究所，湖北 武汉，430081)

炼钢-连铸生产过程是现代钢铁产品制造的重要环节。目前对于炼钢-连铸生产调度的研究通常基于理想条件，忽略了生产过程中可能发生的不确定事件。如果面对复杂或可变的生产状况，如机器故障、炉次延迟等，确定条件下的调度方案就会变得低效甚至不可行，需要重新制定调度方案以响应生产状况的变动，即进行重调度。快速有效地制定出新的调度计划，对于保证钢铁企业的生产稳定和产品质量具有重要意义。

炼钢-连铸生产重调度问题已受到国内外研究人员的广泛关注。Roy等[1]将知识模型应用于炼钢-连铸生产过程中的调度扰动管理。Yu等[2-3]研究了炼钢-连铸生产过程中的操作时间延迟扰动问题，并提出了操作时间延迟扰动的预测方法。Yu等[4]还进一步研究了炼钢-连铸生产中的作业开始时间延迟扰动导致的生产中断，并对其后果和应对策略进行了全面分析，然而以上针对操作时间延迟扰动所建立的模型并不适用于机器故障问题。Mao等[5]研究了炼钢和精炼阶段出现机器故障的炼钢-连铸生产重调度问题，并采用拉格朗日松弛法进行求解。在上述文献中，均未针对连铸机故障下的炼钢-连铸生产重调度问题提出有效方法。

连铸机故障是炼钢-连铸生产调度中时常会出现的一类具有代表性的复杂大扰动事件，其对原调度方案的影响比较大，甚至会影响浇次计划[6]，因此连铸机故障下的生产重调度研究十分重要。王柏琳等[7]针对该问题建立了动态约束满足模型, 将模型分为连铸方案修复子模型和炼钢精炼重调度子模型，并提出了基于约束满足的优化方法。Long等[8]对故障连铸机上的炉次采用人工指派的策略进行处理，然后建立数学模型并设计一种改进遗传算法进行求解。

基于上述研究，本文首先总结4种连铸机故障下的炉次重分配策略及其对重调度的影响；其次提出一种智能分配启发式规则，来完成故障连铸机上炉次的重分配；然后构建一个重调度模型，可以在连铸机故障状况下生成新的调度方案；再将启发式规则融入改进遗传算法中求解模型；最后通过源于生产实际的调度案例来验证所提出方法的有效性。

1 考虑连铸机故障的炼钢-连铸重调度问题

1.1 问题描述

炼钢-连铸生产过程主要分为3个阶段：炼钢、精炼、连铸，如图1所示。连铸机是炼钢-连铸生产工艺中唯一以批为单位、批内连续工作的设备，其任务是将钢水凝固成板坯[9]。在实际生产中，由于钢水温度过低而水口结瘤、铸坯质量问题、上游补料延迟等原因会导致连铸机故障，不能继续进行作业。此时故障机器上正在进行浇铸或即将开浇的浇次中的各个炉次需要进行重分配。

将未完成的炉次分配到同一阶段的其他机器上是一种常见的炼钢-连铸重调度策略[5]，但这种策略仅适用于炼钢和精炼阶段设备故障下的重调度，却无法满足连铸机故障下的生产调度特点。因为连铸阶段的作业是一个连续过程，且其具有以浇次为单元进行批量加工的特殊工艺特征。浇次内能够连浇的炉次的钢种必须兼容，否则会产生连浇成本。因此，为了最大限度地降低连浇成本，在计划阶段已经预先确定了每一浇次中每一炉次的浇铸顺序。连铸机发生故障后，在进行重调度时需要重新确定故障连铸机上每个炉次正在加工和还未开始操作的连铸机分配和加工顺序。

1.2 故障连铸机上的炉次重分配常用策略

在实际生产中，常用以下策略处理故障连铸机上的炉次。

(1)改派：(a)在故障发生时，若故障机上所中断浇次内的炉次正处于炼钢或精炼加工，且该浇次与非故障机上指定浇次钢级相同，可将该炉次重新指派到相关浇次，无需改变钢水成分；(b)在故障发生时，若故障机上所中断浇次内的炉次正在浇铸，其与非故障机上钢水成分相同，则可将相关炉次剩余钢水直接插入到相关浇次中；当钢级相近但兼容时，存在钢级转换成本。

(2)改性：在故障发生时，故障机上中断浇次内的炉次已完成精炼操作，且钢水成分、钢水的液相线温度与其他铸机上钢水属性不合，则通过改变炼钢和精炼阶段的加工路线，即返送回炼钢或精炼炉，达到改变其化学成分的目的，然后将其插入到另一个非故障连铸机上的浇次中。

(3)等待：在故障发生时，故障机上还未开始下一浇次的浇铸且故障机停机时间不长，无需改变浇次计划，不必进行炉次重分配。

(4)报废：故障发生时，若故障机上中断浇次内的炉次无法采取上述任一措施，则撤销该炉次的生产任务，钢水报废。该策略在实际生产中很少用到。

考虑到上述分配策略对生产稳定性的影响，规定其优先级关系为：等待>改派>改性>报废。

1.3 炉次重分配规则

由于在炼钢过程中炉次中钢水的温度不能低于其液相线温度，即等待时间不能过长，因此本文采用基于等待时间最小化的炉次重分配规则，如图2所示。

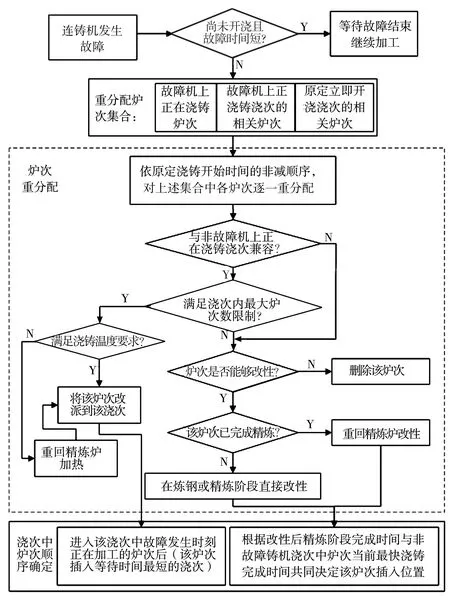
图2 炉次重分配规则

在进行炉次重分配时，需注意以下条件：①在制定重调度计划时，每个浇次存在浇次内最大炉次数的限制；②如果决定改变一个炉次的化学成分，那么重调度时可在炼钢或精炼阶段相应地改变其成分，而已经完成精炼的炉次，则只能重回精炼炉，改变其成分；③为保证温度要求，部分炉次需要回精炼阶段重新加热；④如果炉次的生产任务被取消，则所有已完成的操作应保留在新的计划中，而后续操作应取消。

基于上述准则，将所有需要进行重分配的炉次构成一个集合。在该集合中，依照各炉次原定浇铸开始时间的非减顺序，逐个进行重分配策略判定，继而确定其在新浇次中所处的炉次顺序。

2 基于炉次重分配的生产重调度模型

当连铸机发生故障时，炼钢-连铸生产的每道工序处在三种状态之一：已完成、正在进行和未开始。如果一个炉次的所有工序都已完成，称其为已完成炉次；如果某炉次的某道工序正在进行或仍有工序未开始，称其为正在加工炉次；如果某炉次所有工序都未开始，称其为未开始炉次；将正在加工炉次和未开始炉次统称为还未完成炉次。

基于上述思想，并假定已重新分配各炉次所属浇次，且相关炉次在规定浇次内的顺序已定，则连铸机故障时生产重调度模型构建如下。

2.1 符号说明

s阶段序号，s∈{1,2,…,S}。

m机器序号，m∈{1,2,…,M}。

Ms阶段s的机器集合。

i炉次序号，i∈{1,2,…,I}。

k浇次序号，k∈{1,2,…,K}。

oi炉次i的操作序号，oi∈{1,2,…,O(i)}。

soioi操作的阶段序号。

tsoi炉次i在阶段s的oi操作的加工时间。

βoi重调度开始时刻操作oi的生产状态标志。如果操作oi还未开始，则βoi=0；如果操作oi正在进行，则βoi=1；如果操作oi已经完成，则βoi=2。

ψ 包含所有需要重调度的炉次集合，即故障发生时刻已开始加工浇次内的炉次，以及还未开始的其他浇次。

Ωm铸机m上所有浇次集合。

Ik浇次重组后第k浇次中所有炉次集合，|Ik|表示浇次内总炉次数。

lb(k) 第k浇次中第一炉的炉次序号。

le(k) 第k浇次中最后一炉的炉次序号。

re同一连铸机上相邻两浇次间的准备时间。

st′oi初始调度中炉次i的操作oi的开始时间。

et′oi初始调度中炉次i的操作oi的完成时间。

y′m,oi在初始调度中炉次i的操作oi分配给机器m加工则为1，否则为0。

U足够大的正整数。

λ目标函数权重。

重调度决策变量：

ym,oi0-1变量。当且仅当炉次i的操作oi在机器m上加工时为1，否则为0。

zm,i,i′0-1变量。当且仅当炉次i和i′在机器m上加工且i先加工时为1，否则为0。

stoi重调度后炉次i的操作oi的开始时间。

etoi重调度后炉次i的操作oi的完成时间。

2.2 重调度时刻的状态描述

当机器发生故障时，已开始但未完工的炉次只可能处于两种状态：正在某设备上加工和等待加工。对于正在设备上加工的炉次，即当βoi=1时，stoi=st′oi,ym,oi=y′m,oi,∀i∈ψ,∀m∈{1,2,…,M},∀oi∈{1,2,…,O(i)}，还需要确定下一个操作的加工设备以及在该设备上的开始和结束时间。对于等待加工的炉次，即当βoi=0时，在重调度中只需确定其下一个操作的加工设备以及在该设备上的开始和结束时间。对于已经完成的炉次,在重调度中不需改变其状态，即当βoi=2时，stoi=st′oi,etot=et′oi,ym,oi=y′m,oi,∀i∈ψ,∀m∈{1,2,…,M},∀oi∈{1,2,…,O(i)}。

2.3 假设条件与模型构建

基于以上描述和分析，在本节中建立连铸机故障下的炼钢-连铸生产重调度问题数学模型。以下为模型假设：①初始调度是已知的，其中包括每一阶段所指派的机器分配、加工顺序以及在各个机器上的加工时间；②重调度的对象是故障发生时刻最后一个阶段尚未加工完的已开始浇次或未开始浇次内的所有炉次；③每一炉次在各阶段的加工设备上的加工时间已知；④各炉次的加工工艺路径确定；⑤一个重组浇次内的炉次必须连浇连铸；⑥调度过程中运输时间包含在相应的操作时间内。

炼钢-连铸生产重调度需要同时兼顾两个目标：最小化最大完工时间和最小化各炉次的总流程时间。前一目的是保证生产效率，后一目的是缩短钢水的周转时间，减少能量损失。由于二者之间存在量纲差异，为简化目标函数，分别对其进行归一化处理，详情如式(1)～式(3)所示。

f1=Cmax

(1)

(2)

(3)

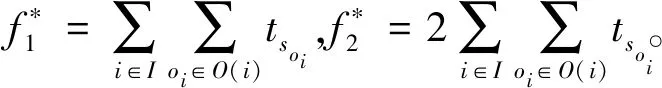
∀i∈ψ,∀oi∈{1,2,…,O(i)-1}

(4)

zm,i,i′+zm,i′,i=ym,oiym,oi′,

∀(i≠i′)∈ψ,∀m∈{1,2,…,M},

∀oi∈{1,2,…,O(i)-1}

(5)

stoi+1-etoi≥0,

∀i∈ψ,∀oi∈{1,2,…,O(i)-1}

(6)

sto′i′-etoi+(3-ym,o′i′-ym,oi-zm,i,i′)U≥0,

∀(i≠i′)∈ψ,∀m∈{1,2,…,M},

∀oi∈{1,2,…,O(i)-1},

∀o′i′∈{1,2,…,O(i′)-1}

(7)

etO(i)+re≤stO(i′),i=le(k),i′=lb(k+1),

∀k∈{1,2,…,|Ωm|-1}

(8)

etO(i)=stO(i+1),

∀(i,i+1)∈Ik,∀k∈{1,2,…,K}

(9)

Cmax≥etO(i),∀i∈{1，2，…，I}

(10)

ym,O(i)=1,∀i∈Ik,k∈Ωm,m∈Ms

(11)

stoi≥0,etoi≥0,

∀i∈ψ,∀oi∈{1,2,…,O(i)}

(12)

ym,oi∈{0,1},∀i∈ψ,∀oi∈{1,2,…,O(i)},

∀m∈{1,2,…,M}

(13)

zm,i,i′∈{0,1},∀(i≠i′)∈ψ,

∀m∈{1,2,…,M}

(14)

式(4)表示炉次的每一个操作只能进行一次；式(5)表示同一操作中不同炉次存在优先关系约束；式(6)表示同一台机器在同一时刻只能加工一个炉次；式(7)表示炉次前一操作完成，后一操作才能开始；式(8)为相邻两浇次之间的准备时间约束；式(9)为连浇连铸约束；式(10)表示最后一个完成加工的炉次的完成时间不超过最大加工时间；式(11)表示铸机上的炉次分配及加工顺序已知。

3 考虑炉次重分配的重调度算法设计

由于炼钢-连铸生产重调度为NP-hard问题，模型求解较难，因此设计一个改进遗传算法，并加入启发式解码方法进一步优化解的质量。算法的具体流程如图3所示。

3.1 基于倒排的编码及初始化

因为各炉次的连铸机和浇铸顺序已经确定，故连铸阶段调度信息无需加入编码过程。鉴于炉次在连铸机上的分配已定，为了满足浇次内各炉次的连浇约束，在算法设计中采用回溯法倒排[10]方式进行种群的编码和初始化。

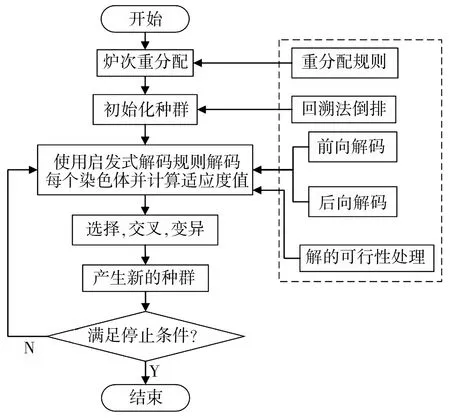
图3 改进遗传算法流程

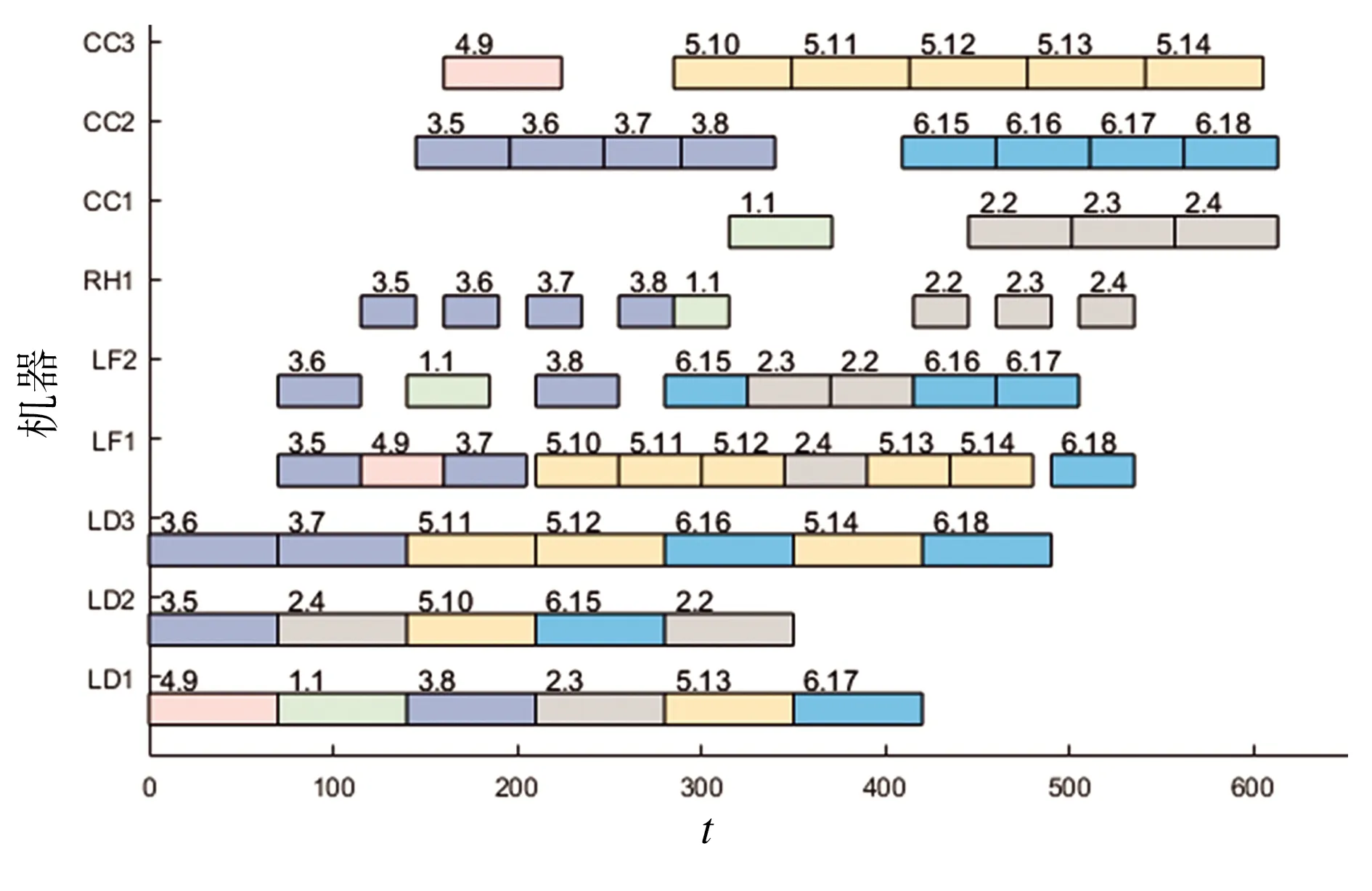
针对炼钢和精炼这两个阶段，采用双段整数编码，第一段表示全部炉次在炼钢和精炼阶段的加工顺序，第二段表示各炉次在每道工序上的机器序号。由于各炉次已经完成加工部分的信息可以忽略，为了减少编码的冗余性，仅需对未完成加工部分进行编码。以图4为例，连铸机CC2故障发生时刻，各炉次操作呈现出已完成、正在加工、还未开始3种状态。甘特图中灰色部分表示某炉次在该阶段已经完成的操作和机器分配，白色部分表示正在加工的操作和机器分配，红色部分表示还未开始的操作和机器分配。编号“3.8”中，3为浇次序号，8为炉次序号，其余类推。机器分配中，序号1～4分别代表LD1、LD2、LF1、LF2。染色体中，炉次加工顺序编码为(3,4,7,2,8,3,4)，可见炉次(7,2,8)仅需进行精炼操作，而炉次(3,4)尚需炼钢和精炼两种操作。

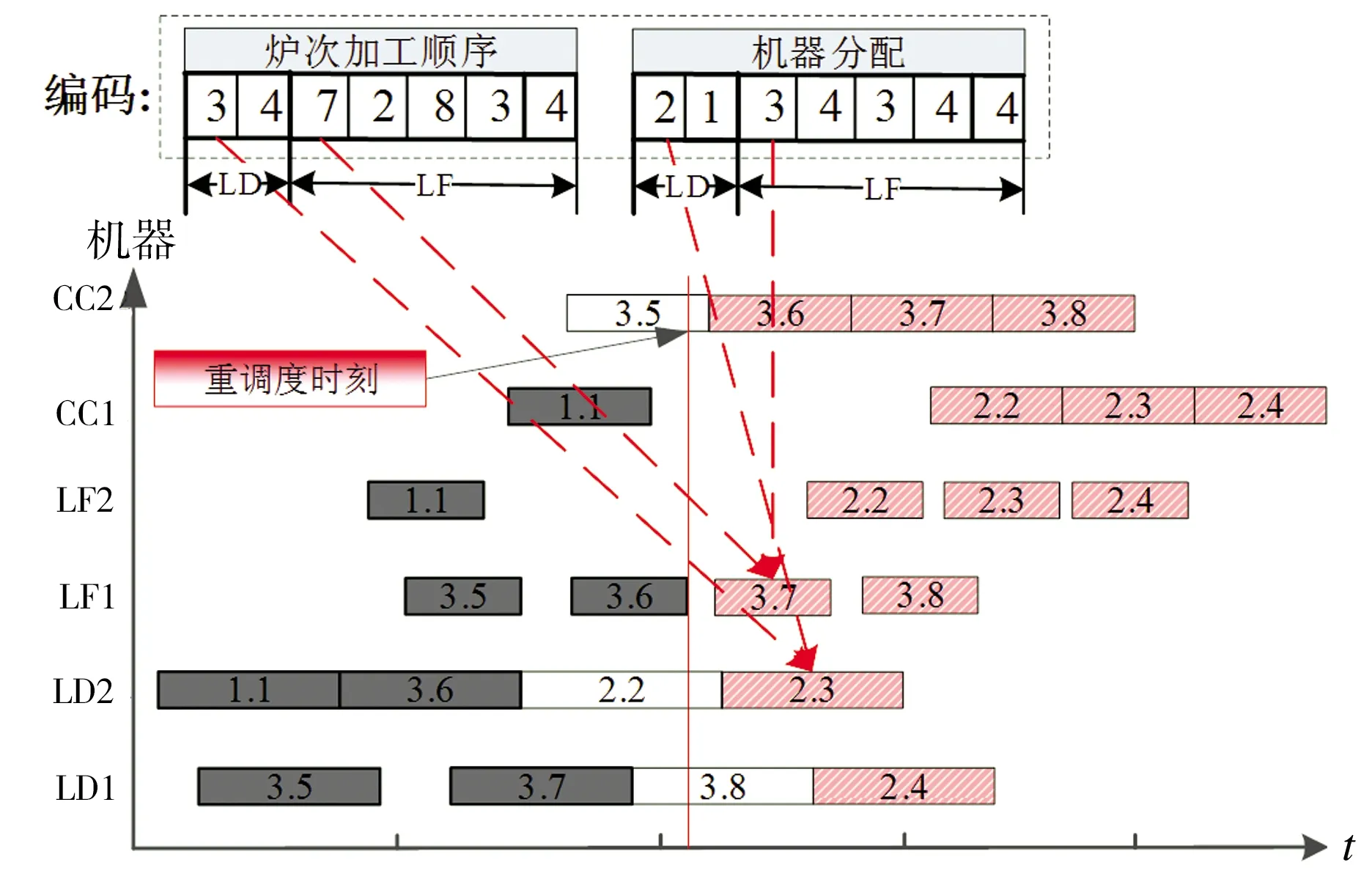
图4 编码示意图

3.2 重调度解码规则

Step1由于故障铸机上炉次的浇铸顺序和机器分配由重分配规则确定，而其他炉次的浇铸顺序在初始计划中已经确定，因此解码时只需要确定连铸机上炉次的开始与结束时间。具体方法是，首先确定每个浇次的开浇时间和浇次内炉次的加工时间，然后根据约束条件(8)和(9)即可确定连铸阶段各炉次的开始和结束时间，其中，已完成浇铸的炉次信息已知。由此就可以得到连铸阶段的调度信息，进入下一步。

Step2依照所有炉次最后阶段开始时间的非减顺序，构建炉次序列ξ。

Step3从序列ξ中取出第一个炉次i，如果该炉次是正在加工的炉次，进入Step 4，否则进入Step 5。

Step4使用“前向解码”，即从炼钢阶段开始，顺推各炉次在各阶段的开始、结束时间和机器分配。

Step4.1令oi=1;

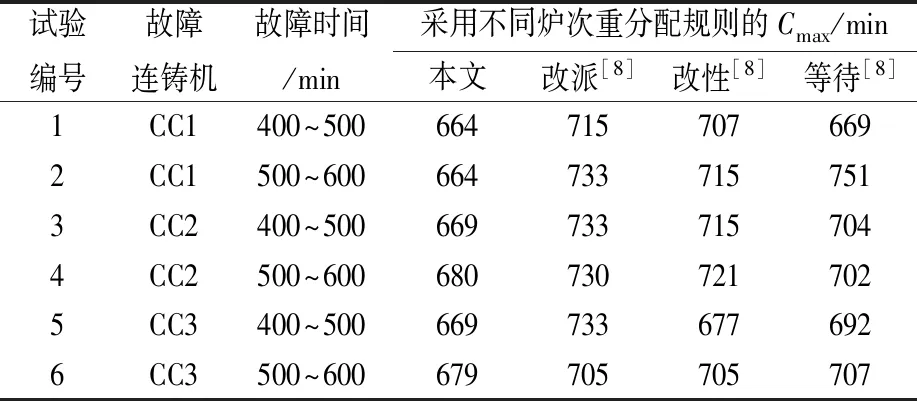
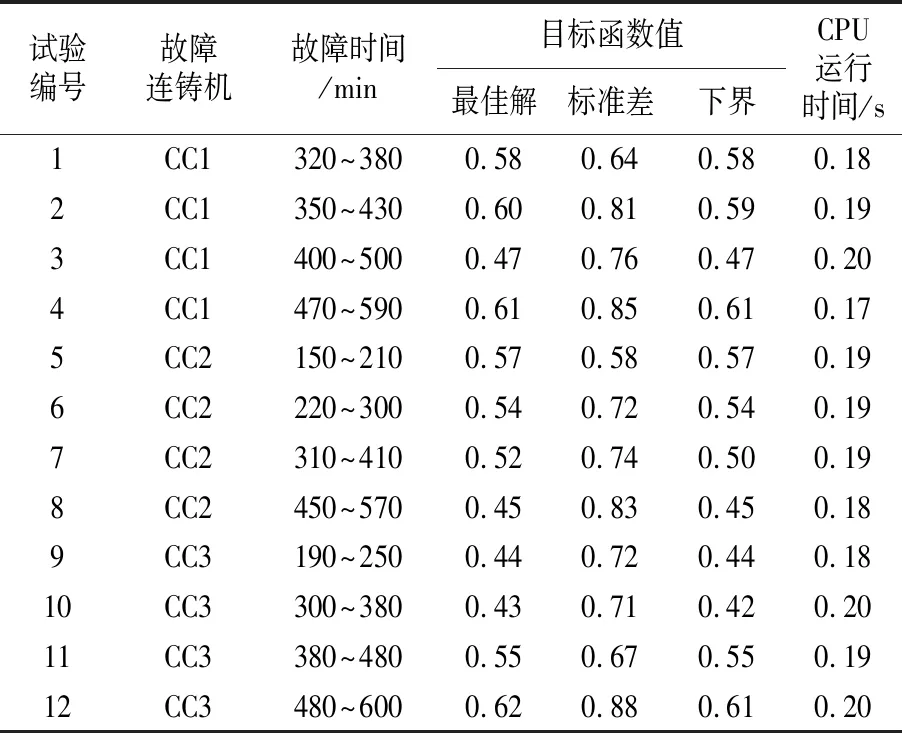
Step4.2如果oi

Step4.3如果βoi≠2,则进入Step 4.4，否则令stoi=st′oi,etoi=et′oi,moi=m′oi,机器moi加工下一炉次的最早可用时间更新为ηm=etoi,然后进入Step 4.6；

Step4.4如果βoi≠1,则进入Step 4.5,否则令stoi=st′oi,moi=m′oi,etoi=stoi+tsoi,机器moi加工下一炉次的最早可用时间更新为ηm=etoi，然后进入Step 4.6；

Step4.5如果βoi≠0,则进入Step 4.6,否则找出etoi-1和moi-1，令stoi=max{etoi-1,ηm},etoi=stoi+tsoi,机器moi加工下一炉次的最早可用时间更新为ηm=etoi，然后进入Step 4.6；

Step4.6令oi=oi+1,返回Step 4.2。

Step5使用“后向解码”，从连铸阶段开始，倒推能满足连浇连铸约束的各炉次开始和结束时间。

Step5.1令oi=O(i)-1;

Step5.2如果oi≥1，则进入Step 5.3，否则进入Step 6;

Step5.3找出stoi+1和moi+1，令etoi=stoi+1,stoi=max{etoi-tsoi,ηm},机器moi加工下一炉次的最早可用时间更新为ηm=etoi;

Step5.4令oi=oi-1,返回Step 5.2。

Step6从序列ξ中删除第一个炉次i，如果ξ为空，结束算法，否则返回Step 3。

3.3 算子设计

采用轮盘赌法进行选择操作，并采用精英策略将最好的父代复制给子代。由于重调度对已完成加工的炉次的操作不予改变，因此对于一个染色体，将以大概率优先选择直接受到连铸机故障影响的炉次进行交叉和变异操作。交叉操作采用整数分段式交叉，即对于炉次的加工顺序和机器分配分别进行交叉操作。变异过程为：①随机产生一个非负数；②在染色体中随机选择一个基因位置，改变等位基因；③重复上一步骤，直到变异基因的数目等于随机产生的非负数。

3.4 考虑可行性的适应度值计算

在交叉、变异过程中，新产生的解可能不可行，例如某炉次重复次数与所需操作数不等。为淘汰不可行解，对其进行惩罚，即根据下式计算适应度值：

(15)

式中：f(x)为x的目标函数值；R是足够大的惩罚系数；0-1变量Vi(x)刻画调度计划的可行性，Vi(x)=0时，x中炉次i为可行解，否则为不可行解。

4 实验与结果分析

为了验证本文模型与算法是否可行，从现场采集某炼钢厂的实际生产数据进行对比实验分析。结合该厂日常生产钢种信息，选取了较具代表性的Q235钢种常规等级的薄板坯加工任务订单，其生产设备信息如下：炼钢阶段，LD炉3台，加工时间为70 min/台；精炼阶段，LF炉2台，加工时间为45 min/台，RH炉1台，加工时间为30～40 min/台；连铸阶段，连铸机(CC)3台，加工时间为51～64 min/台。

对于给定的一个浇次计划k∈{1,2,3,4,5,6}，依次执行下列过程(见图5)，其中精炼阶段有钢包处理和真空处理两种不同的工艺，且每种工艺相互独立。

图5 初始调度甘特图

为了对比分析的有效性，本实验只考虑同一种板型Q235钢种的薄板坯订单任务，并同时调用中板坯和薄板坯3台铸机。具体参数有：阶段s∈{1,2,3,4}，每阶段机器集合Ms={3,2,1,3}，浇次数k∈{1,2,3,4,5,6}，浇次内的炉次数Ik={1,3,4,1,5,4}。其中，浇次1、2、3为特殊要求订单，需要经过两重精炼，其他浇次均为一重精炼。调度任务即对6个浇次18个炉次的订单任务进行计划排产，生产设备总数M=9台。各炉次在不同阶段的加工时间是固定的，连铸阶段相邻浇次之间需要一定的准备时间，但各炉次的连铸时间却各不相同，要根据具体的炉容量和浇次而定。浇次间准备时间re=60 min。为了便于比较，目标函数中权重系数均取λ=0.4。

实验采用MATLAB编程，PC运行环境：2.6 GHz CPU和4 GB内存。为了与所提出的改进遗传算法进行比较，本文还采用CPLEX软件对模型求解，由于其求解速度较慢，CPU运行终止时间设定为5 min，运行环境同上。

由于遗传算法性能受参数影响较大，故需要通过多因素方差分析确定最优的参数组合。种群规模、交叉概率、变异概率各考虑3个参数水平，种群规模设为(20,40,60)，交叉概率设为(0.7,0.8,0.9)，变异概率设为(0.1,0.2,0.3)。设计正交试验，对每个参数组合单独运行10次，取其平均值作为最终结果，然后用Minitab软件对所求结果进行方差分析。结果表明，3个参数对目标函数的影响程度从高到低依次为：种群规模>交叉概率>变异概率，最终选取的参数水平为：种群规模40，交叉概率0.7，变异概率0.3。

假设连铸机CC3在400 min时发生故障，500 min时可以再次投入使用。图6所示为融入了重分配规则的改进遗传算法的模型求解结果。图中深灰色部分表示当CC3发生故障时已经完成的炉次，红色部分表示连铸机故障持续时间。通过实验可以得出，调度计划中不存在时间冲突和非故障机浇次中断，因此，当炼钢-连铸生产过程中出现连铸机故障导致原调度计划不可行时，运用该算法可以得到较好的解决方案。

为了验证本文提出的炉次重分配规则的有效性，将融入该规则的重调度最大完工时间(Cmax)与文献[8]中采用单一的人工指派策略分配故障机上炉次的Cmax进行对比，试验结果如表1所示。

表1 不同炉次重分配规则的比较

从表1中可以看出，与人工分配策略相比，在重调度过程中融入所提出的重分配规则后，所获得的最大完工时间明显缩短。

考虑到影响调度结果的主要因素为故障机器、故障发生时刻以及故障持续时间, 为进一步验证算法的有效性和求解质量，共生成12组对比试验案例，其中故障开始和结束时间随机生成，开始时间区间为[150,480]，结束时间区间为[210,600]。为了保证实验的公平性与准确性，每组实验均采用相同迭代次数作为终止条件，并将本文算法所得最佳解与通过CPLEX软件在给定时间内获得的解(即下界)进行对比，实验结果见表2。

表2 本文算法的性能测试指标

由表2可见，采用融合重分配规则的遗传算法所求最佳解与下界值基本一致，每个案例求解时间不超过0.2 s，表明本文算法的计算效率较高，能够实时响应连铸机故障的扰动事件，快速给出可行的新方案，从而满足实际生产调度要求。

5 结语

在炼钢-连铸生产过程中，不同于其他机器故障，连铸机故障下的重调度首先需为故障机上每个未完成炉次重新分配浇铸顺序和连铸机。因此，本文参考实际生产中调度人员经常使用的炉次重分配策略，提出了一种基于等待时间最小化的启发式规则对故障连铸机上的炉次进行重分配。基于重分配后的炉次浇铸顺序与连铸机安排建立了重调度模型，以便生成新的调度计划。然后设计了融合重分配规则的改进遗传算法求解该模型。最后通过来源于实际生产中的算例验证了所提出的方法在连铸机故障时进行生产重调度的有效性。