实正态过程之均方积分过程的正态性

吕 芳

(洛阳师范学院数学科学学院， 河南洛阳 471934)

1 基本概念

定义1[1,2]设{X(t),t∈T}是一个随机过程， 如果对于任意n≥1和任意t1,t2,…,tn∈T， (X(t1),X(t2),…,X(tn))是n维正态随机向量， 则称{X(t),t∈T}为正态过程或高斯过程.

将概率空间(Ω,F,P)上具有二阶矩的随机变量的全体记为H.

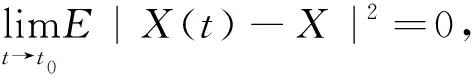
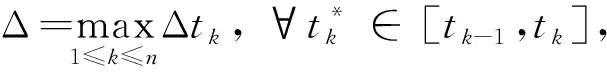
2 相关定理

定理1[5]设m维随机向量X=(X1,X2,……,Xm)～N(μ,B)， 若n维随机向量Y是X的线性变换， 即Y=XC， 其中C是m×n阶矩阵， 则Y服从n维正态分布N(μC,CTBC).

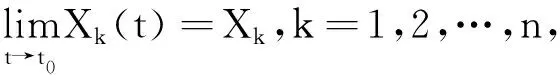
引理1[6]设X=(X1,X2,……,Xn)是n维随机向量，X～N(μ,B)， 其中μ为均值向量，B为协方差矩阵， 则X的特征函数为

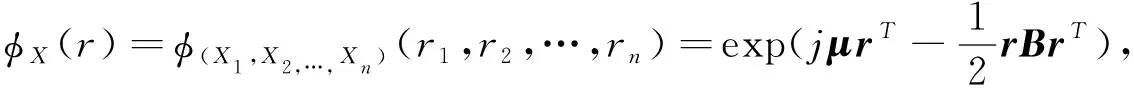
由引理1及正态过程的定义易得定理3.

定理3设{X(t),t∈T}为正态过程， 均值函数为mX(t),协方差函数为CX(s,t),则{X(t),t∈T}的任意有限维特征函数为

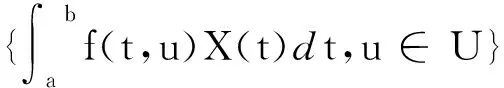
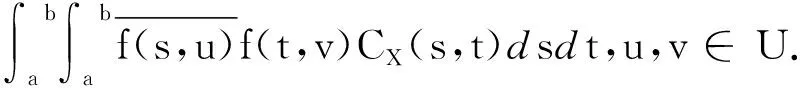
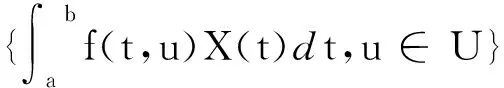
相关函数为

故协方差函数为

3 主要结论

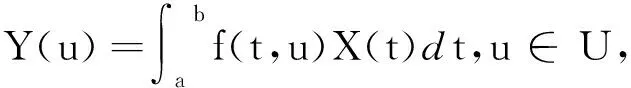
ri∈R,ui∈U,i=1,2,…n,n∈N.

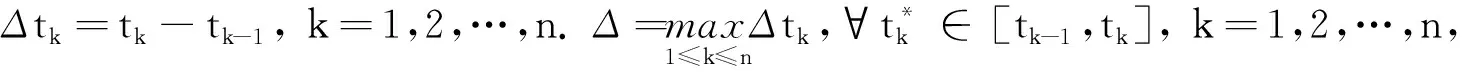
于是， ∀m≥1， ∀u1,…,um∈U， 有

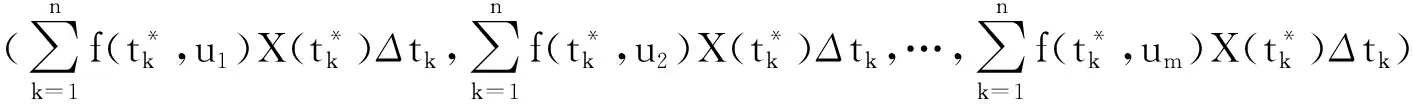
因

(Y(u1),Y(u2),…,Y(um))

由定理2知(Y(u1),Y(u2),…,Y(um))是m维正态随机向量， 故{Y(u),u∈U}为实正态过程.

由定理4知均方积分过程{Y(u),u∈U}的均值函数为

协方差函数为

结合定理3得实正态过程{Y(u),u∈U}的任意有限维特征函数为

ri∈R,ui∈U,i=1,2,…n,n∈N.