混凝土坝瞬溃对水库水力学研究
2020-08-01张晓刚
张晓刚
(大石桥市水利事务中心,辽宁 大石桥 115100 )
1 概 述
随着国家科学技术的发展,我国在水利工程领域的发展也是飞速进行,大批水利工程的修建改善了河道的水利通航、水力发电、生态环境改善。但随着大坝修建的年限增长,大坝老化及受到自然灾害的冲击都有可能发生溃决。目前,研究溃坝主要有物理模型试验和数值模拟计算,对比物理模型试验,数值模拟相对可重复性强、节约成本、反演程度高[1]。
目前,溃坝洪水计算模型是水力学分析溃坝发生的重要工具,一直备受国内外学者的广泛关注和引用,许多学者对这一问题进行了大量的研究[2-3]。如唐友一通过分析研究得出溃坝溃口瞬时的最大流量 、流量过程线的简化计算方法,适用于河道型水库、湖泊水库的溃坝计算。谢任之[4]通过公式推导给出瞬时全溃、局部溃、逐渐溃的溃坝坝址峰值流量计算“统一公式”,并给出相应的流量参数表。王立辉讨论了梯级水库同时溃和相继溃、底坡等因素对溃坝波在河道传播的影响程度。因此在前人研究的基础上,本文主要通过Flow-3d建立数学模型研究混凝土坝瞬溃的上下游水位、流量变化,以期得到较为可靠的水力学参数,并为混凝土坝瞬溃提供重要的参考基础。
2 试验设计
2.1 数学模型建立
通过CAD建立混凝土坝的几何模型,通过Flow-3d进行模型的验证。根据图1所示,分别设置上游、溃口、下游3处水位波动模拟点,坝高50 m,假定溃口尺寸30×50 m,溃口位于坝体中心溃决条件为坝前水位50 m漫顶溃决,下游水位10 m。
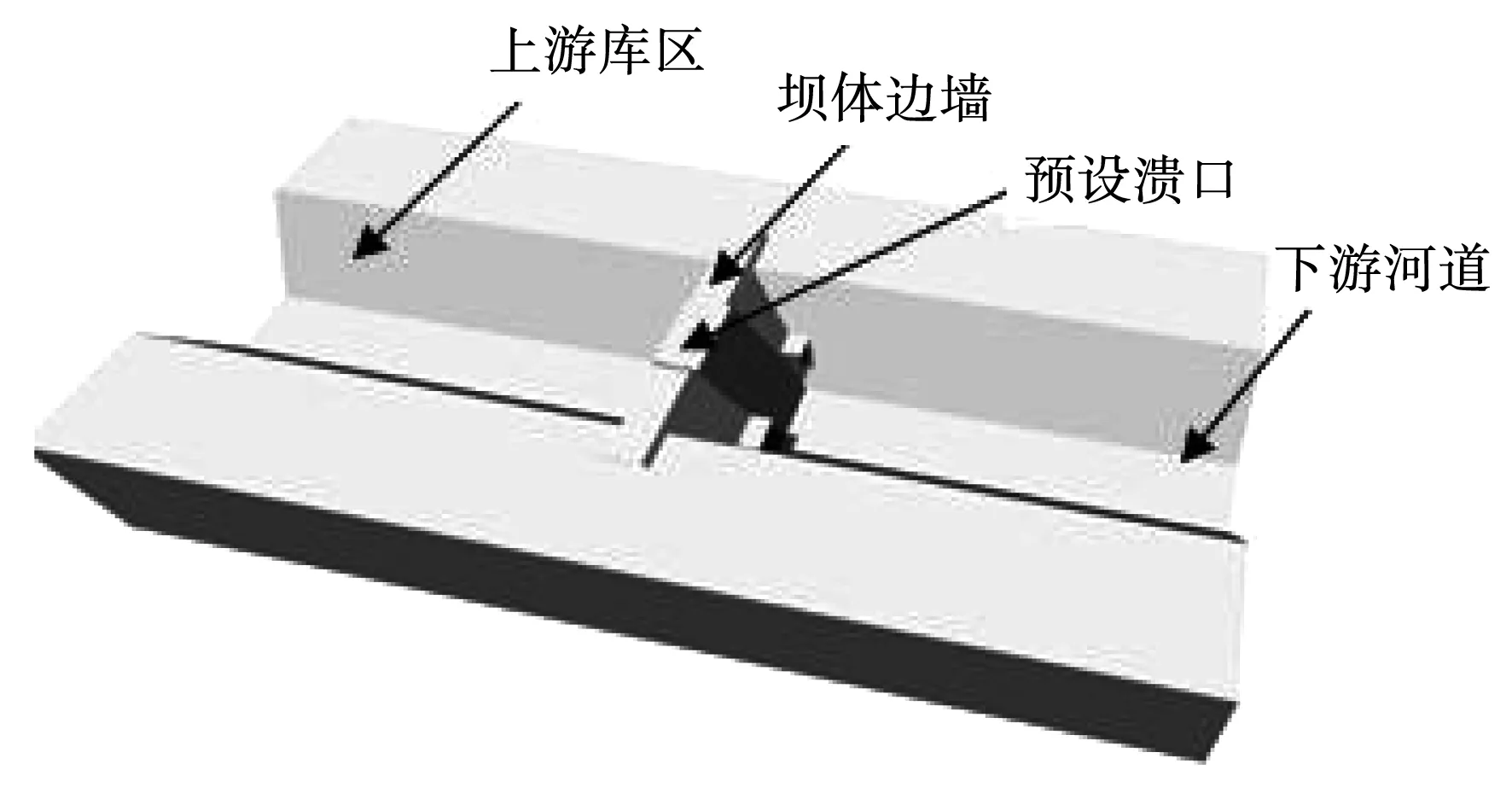
图1 模型布置图
2.2 模型验证
2.2.1 溃决方式
通过建立的数学模型以漫顶溃坝进行模型的验证,即上游水位H=50 m,下游水位H=10 m,预设溃口整体坝高50 cm,假定溃口尺寸30×50 m,具体见图2。

图2 溃口瞬时溃决方式
2.2.2 溃口流速验证
由图3可知,溃口流速的实验值与模拟值在验证的20 s时间内吻合度很高,两者差异小,最大误差为1.2%。数学模型建立的准确可靠,可以作为本文研究的理论基础。

图3 溃口水位对比图
3 混凝土坝瞬溃的数值模拟
3.1 上下游水位
数值模拟混凝土坝瞬溃时,上游监测点在溃口1 m处,下游监测点在溃口3 m处,根据数值模拟结果绘出上下游水位波动图,见图4-图5。由图4和图5可知,在混凝土坝瞬溃的5 s之内上游水位在0.5 s左右时开始下降,在0.5~2 s水位下降缓慢,在第2 s骤然下降较快;下游水位在0.4 s时开始上骤然上升,在1.5 s左右上升到最高点H=30 m,在2.5 s之后缓慢波动水位稳定在H=15 m。

图4 上游水位过程线

图5 下游水位过程线
3.2 溃口流量
模拟溃口流量图见图6。
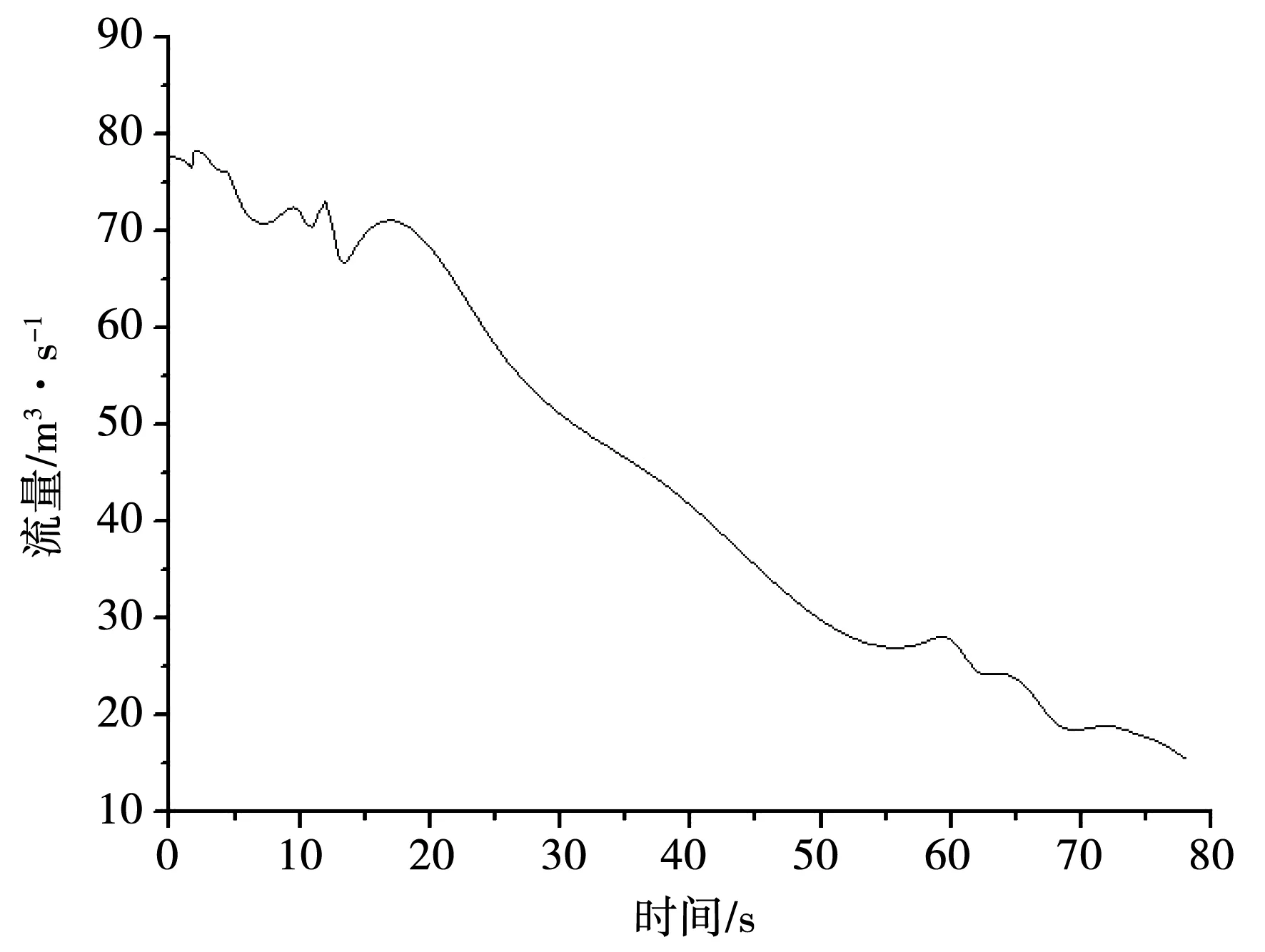
图6 模拟溃口流量图
根据数值模拟值可知,混凝土坝在瞬溃时流量是逐渐降低,在10 s内流量降低的缓慢,10~80 s下降较快,可见混凝土坝在瞬溃时候最佳的封堵时间为瞬溃的1 min之后,在此之前流量及流速较大,封堵难度大且危险。
4 结 论
1) 通过Flow-3d建立混凝土坝的瞬溃模型,根据验证结果可知计算快捷方便、准确可靠,可以计算类似的水力学发生过程,为试验提供相验证的数据。
2) 计算混凝土坝瞬溃时上下游水位波动、溃口流量变化等水力学特性,可见在混凝土坝瞬溃时溃口的流速及流量较大,变化较快。因此,对于混凝土坝在瞬溃时应注重溃口上下游附近的流量、流速及水位的变化情况,采取相应的封堵和救援措施。
