复合式六自由度平台运动学仿真分析
2020-08-01董艇舰武庆余王亚楠
董艇舰,武庆余,王亚楠
(中国民航大学航空工程学院,天津 300300)
六自由度平台是集机械、液压、计算机控制、传感检测和实时信号处理于一体的经典机电一体化系统,可实现空间六个自由度运动,广泛应用于飞机等交通工具的运动模拟[1]。飞行模拟机全动台经典结构采用六自由度并联机构,虽然结构简化到只有6 个作动筒,但其运动耦合和复杂计算所要求的高精密控制系统,极大提升了制造成本。此外平台的运动空间范围(角度小于30°)和平台高度的限制(≥2 m),使得昂贵的全动台只适合特定专业场合,普及度不高。传统的六自由度平台改进研究局限于并联机构架构下布局和尺寸的改进,而混联式六自由度平台可显著提高平台工作空间,文献[2]在并联六自由度平台的基础上,加装回转装置,实现了360°回转。文献[3]将三维线运动与三维角运动相拆分,设计了一种混联式六自由度平台,扩大了平台的运动范围。文献[4]利用混联机构转角可以叠加、转动空间不受位置空间影响的特点,设计了一种满足大姿态、大转角要求的4PRPaRR-3RRR 型混联六自由度平台。文献[5-7]也设计了其他类型的混联六自由度平台。上述设计虽提升了平台工作空间,但依然存在并联机构本身固有的位置正解困难、系统耦合性高、控制复杂以及由此导致的研发成本高等问题,此外文献[4]的设计还存在机构占地空间大的缺点。
基于上述缺陷,设计一种运动空间大、体积小、控制简单、研发成本低的六自由度平台,以满足模拟飞行教学,且具有良好研究价值和市场应用前景。该复合式六自由度平台综合考虑了剪叉机构、回转机构、铰链机构和丝杠导轨的运动特性,将传统的简单机构组合构成复合式运动平台,运用独立串联控制实现升降、回转、平动、俯仰和横滚全部姿态控制。
1 平台结构设计
驱动方式选择是平台设计的关键技术之一,在一定程度上影响平台运动系统的承载能力、运动精度、快速性等运动指标。常用的驱动方式有液压、气压和电动,电驱动去除了液压驱动中液压油的成本,没有复杂的管路和液压阀,无须冷却系统,大大降低了成本[8]。平台负载设计为150 kg,首选电驱动,功率易于保障,易于维护保养,无环境污染。平台立体结构如图1 所示。
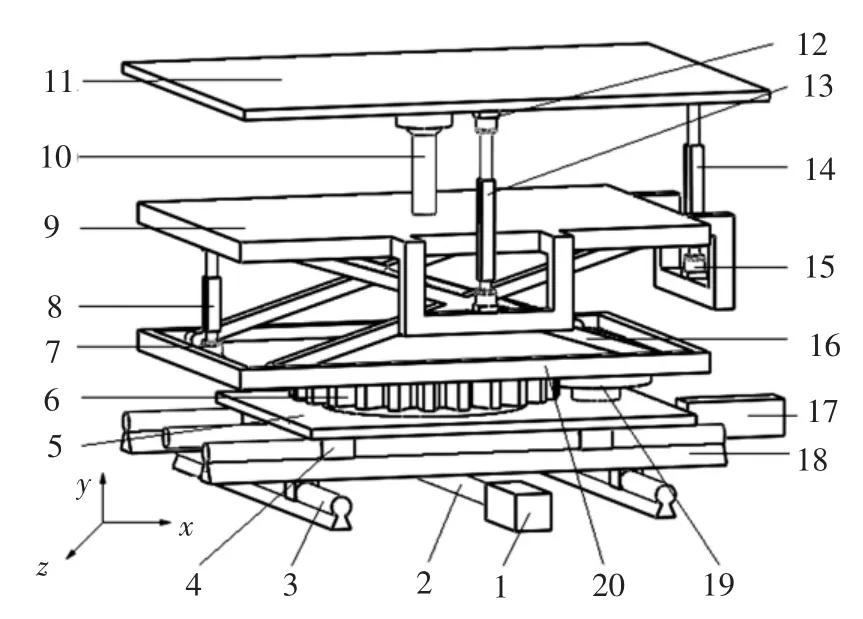
图1 复合式六自由度平台立体结构Fig.1 3D structure of composite six-DOF platform
平台包括平移机构、回转机构、升降机构和翻滚机构,其工作原理为:x 轴电机和y 轴电机分别驱动对应丝杠,使平台在相应导轨上移动,平台实现沿x 轴和y 轴方向的平移。z 轴电动缸驱动剪叉机构,通过剪叉机构的升降,平台实现沿z 轴方向的平移。z 轴电机带动回转支承旋转,平台实现绕z 轴的转动。x 轴电动缸伸缩,驱动平台滚转,平台实现绕x 轴的转动。y 轴电动缸伸缩,驱动平台俯仰,平台实现绕y 轴的转动。
2 平台运动学分析
运动学分析有正反两种求解思路,其中正解是已知连杆几何参数和关节变量,求解末端执行器相对参考坐标系的位置和姿态。反解是已知连杆的几何参数和末端执行器相对参考坐标系的位置和姿态,求解机构达到期望位姿所需的关节变量。采用D-H 参数法[9]作运动学分析,首先建立连杆坐标系和连杆参数表,用于描述相邻连杆间的各种关系,运用矩阵运算和齐次变换建立运动学方程。对于坐标系{n},其原点和x 轴的方向可以任意选取,在选取时应尽量使连杆参数为0。平台连杆坐标系如图2 所示。
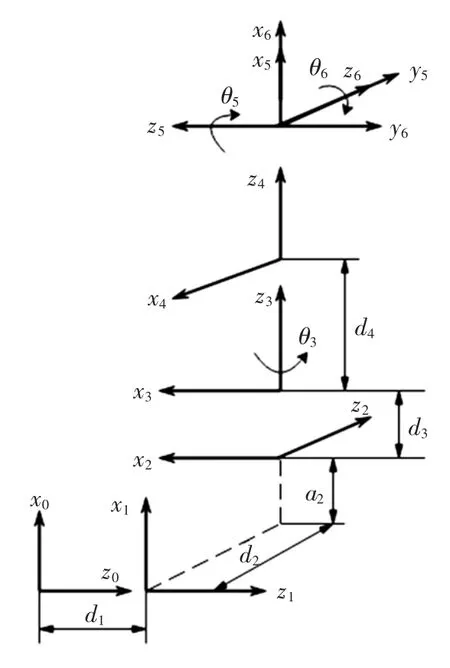
图2 平台连杆坐标系Fig.2 Link coordinate system of platform
由平台连杆坐标系图,列出平台的连杆参数表如表1 所示。
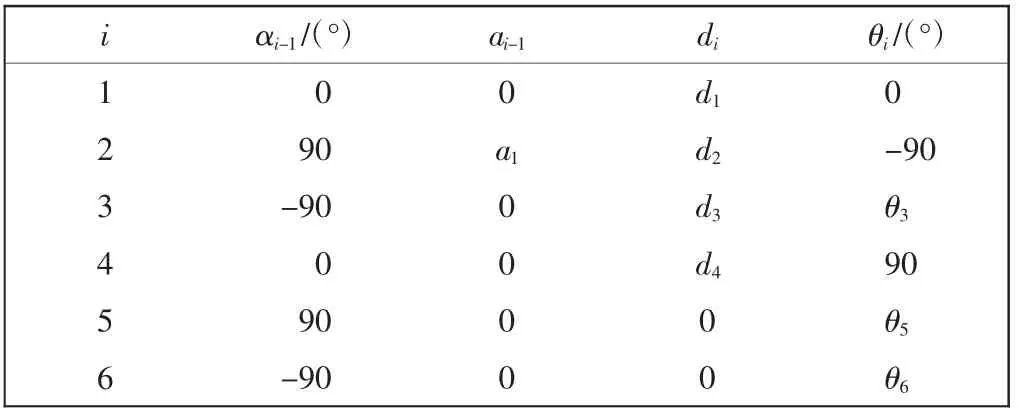
表1 平台连杆参数Tab.1 Platform link parameters
将图2 所示的连杆坐标系{i}中定义的矢量转换为坐标系{i-1}中描述的变换矩阵,即
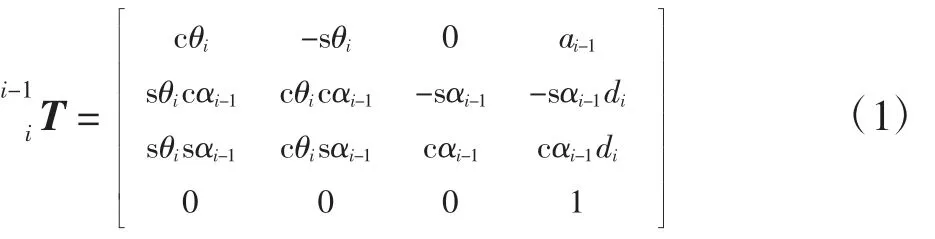
式中:s,c 是sin 和cos 的缩写。
由式(1)和表1 所示的连杆参数表,求得各连杆变换矩阵为
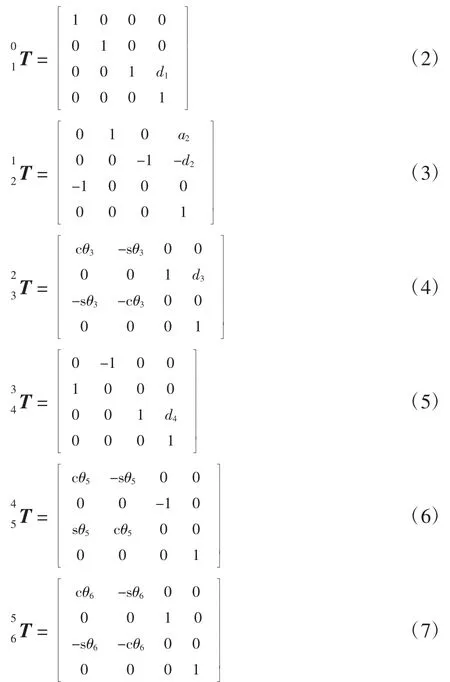
将各连杆变换矩阵相乘,得到运动平台坐标系{6}到基准坐标系{0}的变换矩阵为
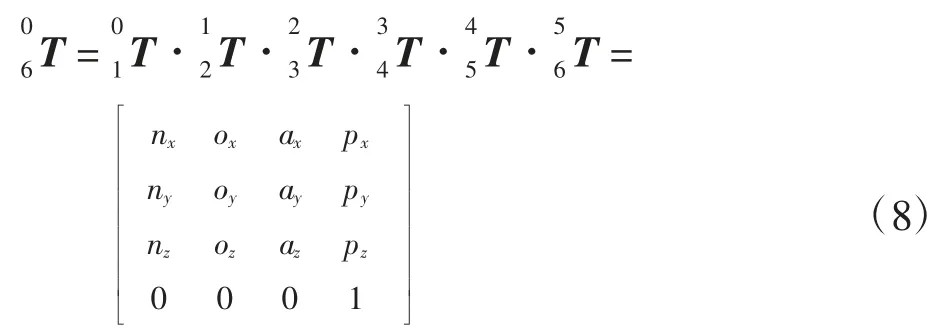
其中
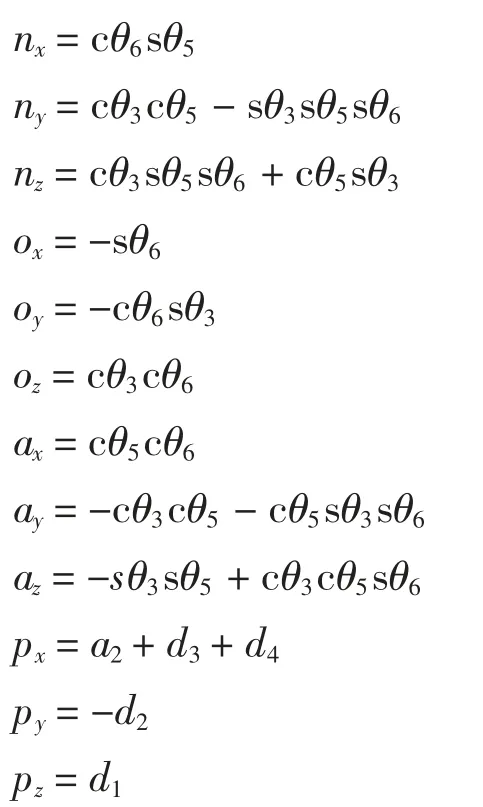
式(8)即为复合式六自由度平台运动学的正解,向量n,o,a 描述了运动平台在基准坐标系{0}中的姿态,向量p 描述了运动平台坐标原点在基准坐标系{0}中的位置。为校验变换矩阵的正确性,将平台初始位置d1=d2=0,θ3=θ6=0°,θ5=90°,d4=170 等代入式(8)得
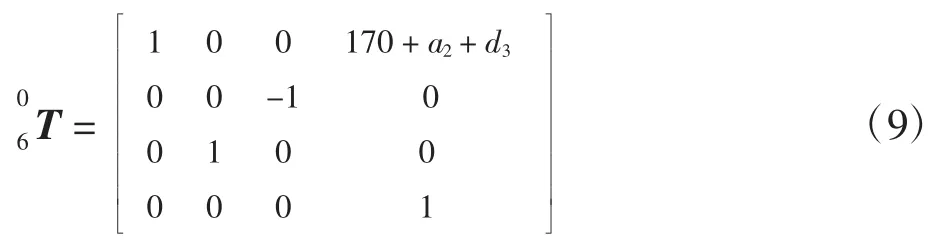
结果与平台初始位姿完全一致,计算结果正确。
平台运动学反解,即式(8)中的向量n,o,a,p 为已知,求解各输入变量θ3,θ5,θ6,d1,d2,d4。反解主要有几何和代数两种解法,此处采用代数解法,从运动学方程入手,求平台运动学反解,得到相对应的连杆参数。式(8)中矩阵元素一一对应,可得平台各输入变量如表2 所示。
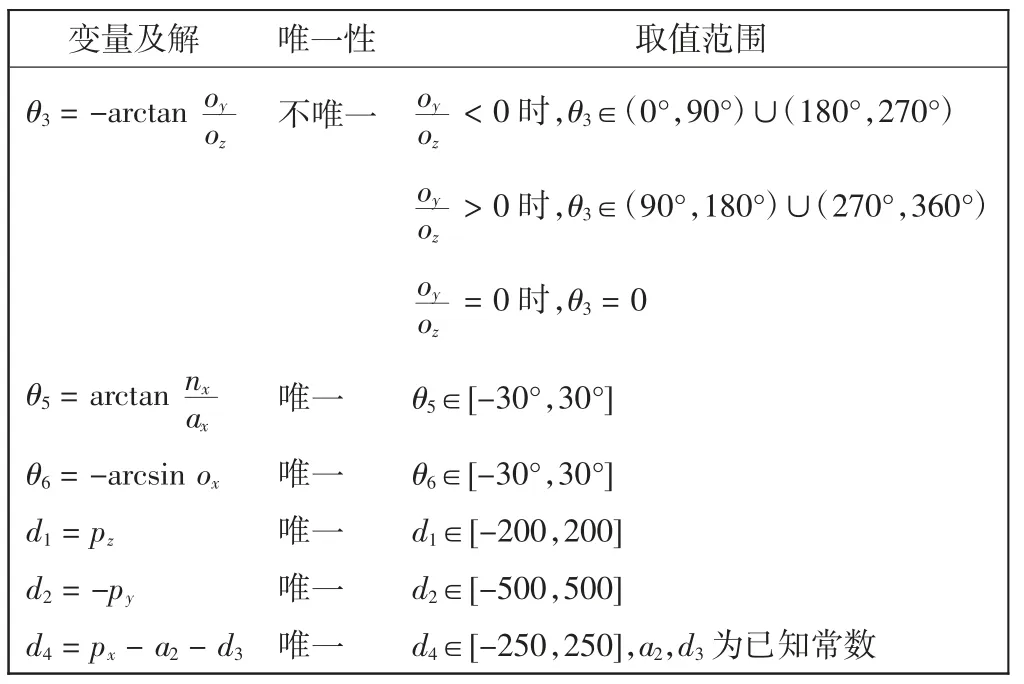
表2 平台运动学反解输入变量Tab.2 Input variables of platform kinematics inverse solution
3 平台运动学仿真
3.1 模型建立
采用SolidWorks 进行三维建模,将模型导入ADAMS 进行运动学仿真,提高仿真精度。首先根据部件形状和尺寸,在SolidWorks 中利用拉伸、旋转、扫描等特征创建方式建立各零件的模型。为保证导入到ADAMS 中的模型方向正确,装配时应注意选取正确的坐标系。为方便装配,将平台装配成若干个子装配体,采用自底而上的装配方法,由子装配体的装配完成整个产品的总装配。全部装配完成后,须做干涉检查,以确保装配体在无干涉情况下作模拟仿真工作。平台SolidWorks 模型如图3 所示。
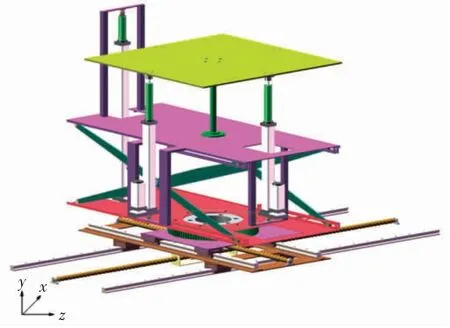
图3 平台SolidWorks 模型Fig.3 SolidWorks model of platform

图4 平台ADAMS 模型Fig.4 ADAMS model of platform
3.2 平台运动学仿真分析
设置仿真时间10 s,步长1 000。仿真完毕后,进入后处理模块,得到运动平台在x,y,z 方向上的位移-时间,速度-时间,角速度-时间,加速度-时间,角加速度-时间曲线分别如图5~图9 所示。
由以上仿真结果可以得出如下结论。

图5 平台位移-时间Fig.5 Platform displacement vs.time
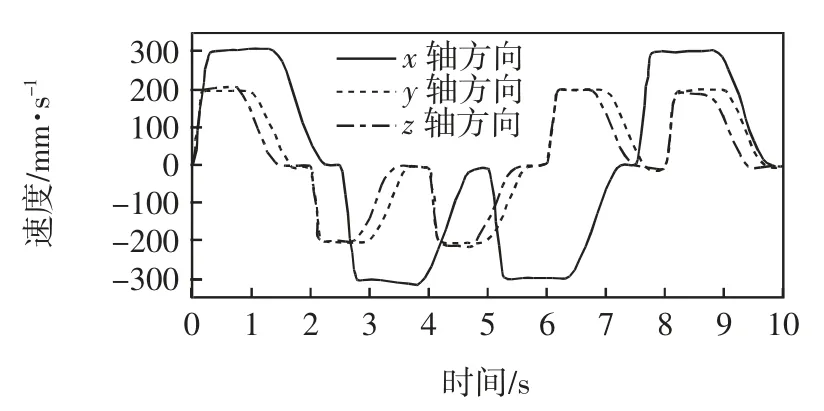
图6 平台速度-时间Fig.6 Platform speed vs.time
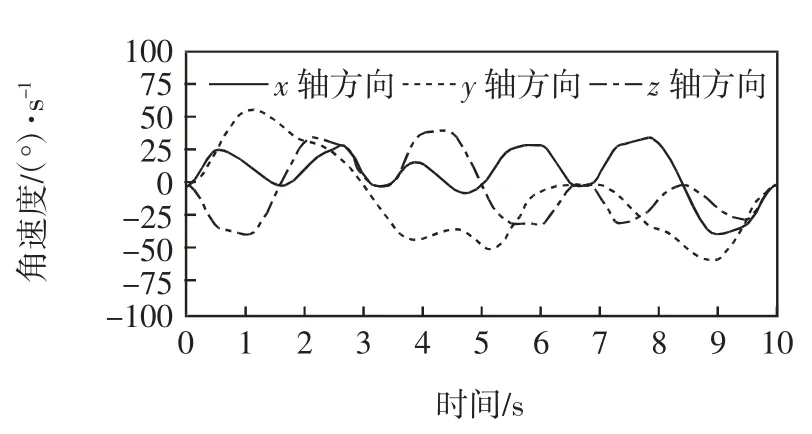
图7 平台角速度-时间Fig.7 Platform angular velocity vs.time
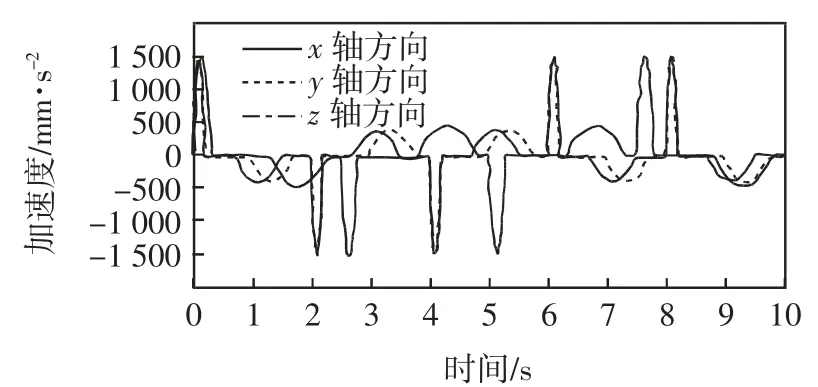
图8 平台加速度-时间Fig.8 Platform acceleration vs.time
模型导入后,验证模型正确性,编辑构件的名称、颜色、位置、材料等属性信息。由于导入后各零部件间的配合关系失效,需在ADAMS 中重新添加运动副,在添加运动副之前,用布尔加将质量属性相同且无相对运动的零部件合为一体。
平台实际运动要经过加速、匀速、减速和静止4个阶段。根据这一特点,采用STEP 阶跃函数控制平台各运动阶段,其格式为STEP(x,x0,h0,x1,h1),其中:x表示时间,x0,x1表示运动初始时间和运动终止时间,h0,h1是对应初始时间和终止时间的函数表达式[10]。根据平台各方向的最大位移、速度、角速度、加速度和角加速度要求,添加相应STEP 驱动函数,完成平台运动学仿真模型建立,如图4 所示。

图9 平台角加速度-时间Fig.9 Platform angular acceleration vs.time
1)平台位移-时间曲线大致呈周期性、中心对称分布,说明平台可重复多次完成同一位姿。由曲线的纵轴可得出平台在3 个方向的最大线位移分别为501.65 mm、253.28 mm、255.36 mm,平台工作空间较Stewart 结构的六自由度平台有了大幅度提高[11]。t=0时,Δdx和Δdz均为0,Δdy为一常数,这一向量[Δdx,Δdy,Δdz]T与式(8)所求平台初始状态的位置向量p 相一致,进一步验证了平台运动学方程的正确性。
2)平台速度-时间和角速度-时间曲线大致呈周期性分布,曲线连续平滑,无明显运动突变,3 个方向的速度均遵循加速-匀速-减速的运动规律,说明运动平台各方向运动特性良好。
3)平台加速度-时间和角加速度-时间曲线无明显突变,说明平台加减速特性良好,运动时无巨大的冲击载荷。平台加速度和角加速度变化范围大,可提供较大的加速度体验,且平台各个方向的最大加速度和角加速度均符合设计要求。较大的加速度需要更大的扭矩和更高的结构强度,因此,该曲线也为平台电动缸的选择、优化设计和强度校核提供了依据。
在平台添加一测量点,得到平台3 个方向的最大角位移分别为31.8°、360°、33.51°。参考同规格并联六自由度平台的运动参数[11],对比复合式六自由度平台和并联六自由度平台工作空间如表3 所示。
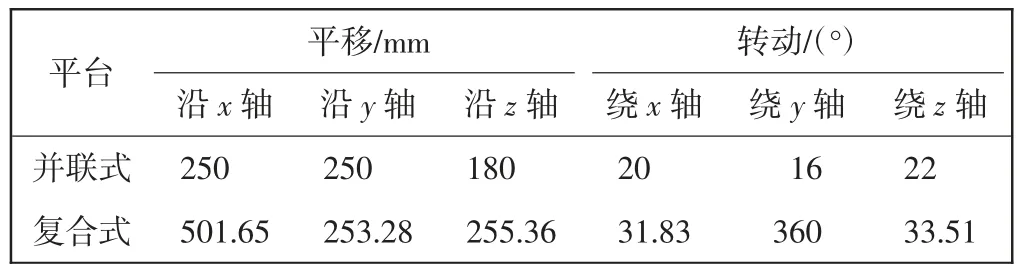
表3 两种平台工作空间对比Tab.3 Workspace comparison between two platforms
可以看出该平台的工作空间较并联式有了大幅提升,3 个方向的线位移分别提升了100.66%、1.31%、41.87%,3 个方向的角位移分别提升了59.15%、2150%、52.32%。此外可以通过增加导轨、丝杠的长度,进一步提高平台的工作空间。
4 结语
采用D-H 参数法建立平台连杆坐标系,求得平台的运动学基本方程和正反解。利用SolidWorks 建立平台三维模型,导入ADAMS 作运动学仿真与分析,得到了平台位移、速度、角速度、加速度、角加速度随时间变化的曲线。结果表明:复合式六自由度平台的工作空间较并联式有了大幅提升;平台具有良好的运动特性,验证了平台结构设计的合理性和运动学分析的正确性。该仿真结果也为平台驱动装置选型计算、后期优化设计和强度校核提供了参考依据。
